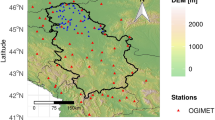
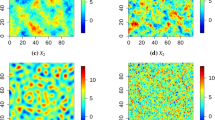
Abstract
Spatial heterogeneity brings numerous uncertainties to training datasets in the modeling process. An arbitrary selection of training samples can result in a biased simulation. Although previous research provides a chance of reducing the degree of spatial variance through homogeneous divisions, detailed information regarding the impact of the configuration of divisions for training remains unknown. Moreover, few studies investigate the cross impact of extreme sampling on non-extreme simulation. Therefore, we extend previous research to investigate the cross impact and further examine whether the divisions of extremely high (EXH) and low (EXL) quantiles contribute equally to the simulation bias when employing the spatial stratified sampling. Statistical assessment demonstrates that the selection of extreme training sample does affect the non-extreme simulation. The model has the best performance (RMSE: 2.735, VE: 7.481, Bias: -0.033) when the least proportion (25%) of EXH and EXL was selected for training. Further analysis also indicated that the EXH and EXL divisions contribute unequally to the process. Particularly, the non-extreme simulation is more sensitive to the EXH training data with a steeper change rate of 0.043. This research provides a critical insight into the extreme point sampling for a machine learning process. Different sensitivity of division calls upon that extreme training sample should be adjusted on a basis of percentage rather than their amounts when applying stratified sampling in Geographical Random Forest.




Similar content being viewed by others
Data availability
Data and materials will be made available on request.
References
Belgiu M, Drăguţ L (2016) Random forest in remote sensing: a review of applications and future directions. ISPRS J Photogrammetry Remote Sens 114:24–31
Berry BJL, Marble DF (1968) Spatial analysis: a reader in statistical geography. Prentice-Hall
Boukerche A, Zheng L, Alfandi O (2020) Outlier detection: methods, models, and classification. ACM Comput Surv (CSUR) 53(3):1–37
Brunsdon C, Fotheringham S, Charlton M (1998) Geographically weighted regression. J Royal Stat Society: Ser D 47(3):431–443
Brus D, De Gruijter J (1997) Random sampling or geostatistical modelling? Choosing between design-based and model-based sampling strategies for soil (with discussion). Geoderma 80(1–2):1–44
Byrd RH, Chin GM, Nocedal J, Wu Y (2012) Sample size selection in optimization methods for machine learning. Math Program 134(1):127–155
Dixon WJ (1950) Analysis of extreme values. Ann Math Stat 21(4):488–506
Dumelle M, Higham M, Ver Hoef JM, Olsen AR, Madsen L (2022) A comparison of design-based and model‐based approaches for finite population spatial sampling and inference. Methods Ecol Evol 13(9):2018–2029
Dunn R, Harrison A (1993) Two-dimensional systematic sampling of land use. J Royal Stat Society: Ser C 42(4):585–601
Flood N, Danaher T, Gill T, Gillingham S (2013) An operational scheme for deriving standardised surface reflectance from Landsat TM/ETM + and SPOT HRG imagery for Eastern Australia. Remote Sens 5(1):83–109
Georganos S, Grippa T, Niang Gadiaga A, Linard C, Lennert M, Vanhuysse S, Kalogirou S (2021) Geographical random forests: a spatial extension of the random forest algorithm to address spatial heterogeneity in remote sensing and population modelling. Geocarto Int 36(2):121–136
Gómez Puente SM, Van Eijck M, Jochems W (2013) A sampled literature review of design-based learning approaches: a search for key characteristics. Int J Technol Des Educ 23:717–732
Gregoire TG (1998) Design-based and model-based inference in survey sampling: appreciating the difference. Can J for Res 28(10):1429–1447
James R, Knaub J (1999) Model-based sampling, inference and imputation
Kalogirou S, Georganos S (2018) Spatial Machine Learning (Version 0.1.3) [Package]
Kwak SK, Kim JH (2017) Statistical data preparation: management of missing values and outliers. Korean J Anesthesiology 70(4):407
Masud MM, Gao J, Khan L, Han J, Thuraisingham B (2008) A practical approach to classify evolving data streams: Training with limited amount of labeled data Paper presented at the 2008 Eighth IEEE International Conference on Data Mining
Millard K, Richardson M (2015) On the importance of training data sample selection in random forest image classification: a case study in peatland ecosystem mapping. Remote Sens 7(7):8489–8515
Myneni R, Maggion S, Iaquinta J, Privette J, Gobron N, Pinty B, Williams D (1995a) Optical remote sensing of vegetation: modeling, caveats, and algorithms. Remote Sens Environ 51(1):169–188
Myneni RB, Hall FG, Sellers PJ, Marshak AL (1995b) The interpretation of spectral vegetation indexes. IEEE Trans Geoscience Remote Sens 33(2):481–486
Sayed A, Ibrahim A (2018) Recent developments in systematic sampling: a review. J Stat Theory Pract 12(2):290–310
Uçar MK, Nour M, Sindi H, Polat K (2020) The effect of training and testing process on machine learning in biomedical datasets. Mathematical Problems in Engineering, 2020
Vabalas A, Gowen E, Poliakoff E, Casson AJ (2019) Machine learning algorithm validation with a limited sample size. PLoS ONE 14(11):e0224365
Wadoux AM-C, Minasny B, McBratney AB (2020) Machine learning for digital soil mapping: applications, challenges and suggested solutions. Earth Sci Rev 210:103359
Wang J, Wise S, Haining R (1997) An integrated regionalization of earthquake, flood, and drought hazards in China. Trans GIS 2(1):25–44
Wang J, Haining R, Cao Z (2010) Sample surveying to estimate the mean of a heterogeneous surface: reducing the error variance through zoning. Int J Geogr Inf Sci 24(4):523–543
Wang J-F, Stein A, Gao B-B, Ge Y (2012) A review of spatial sampling. Spat Stat 2:1–14
Wang H, Seaborn T, Wang Z, Caudill CC, Link TE (2021) Modeling tree canopy height using machine learning over mixed vegetation landscapes. Int J Appl Earth Observation Geoinf 101:102353
Zafari A, Zurita-Milla R, Izquierdo-Verdiguier E (2019) Evaluating the performance of a random forest kernel for land cover classification. Remote Sens 11(5):575
Zeng Y, Hao D, Badgley G, Damm A, Rascher U, Ryu Y, Qiu H (2021) Estimating near-infrared reflectance of vegetation from hyperspectral data. Remote Sens Environ 267:112723
Funding
This publication was made possible by the NSF Idaho EPSCoR Program and by the National Science Foundation under award number OIA1757324. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of NSF. The authors also acknowledge the financial support from the National Natural Science Foundation of China (42202333).
Author information
Authors and Affiliations
Contributions
Hui Wang: Methodology, Data processing, Visualization, Writing-review & editing. Meixu Chen: Writing-review & editing. Zhe Wang: Data processing, Writing-review & editing. Li Huang: Writing-review & editing. Christopher C. Caudill: Supervision, Writing-review & editing. Shijin Qu: Methodology, Visualization, Writing-review & editing. Xiang Que: Writing-review & editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Communicated by H. Babaie.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Wang, H., Chen, M., Wang, Z. et al. How does extreme point sampling affect non-extreme simulation in geographical random forest?. Earth Sci Inform 17, 1983–1991 (2024). https://doi.org/10.1007/s12145-024-01268-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12145-024-01268-9