Skip to main content
SpringerLink
Log in

Events detection and community partition based on probabilistic snapshot for evolutionary social network

  • Published:
Peer-to-Peer Networking and Applications Aims and scope Submit manuscript

Abstract

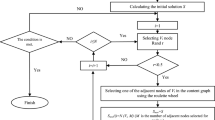
Most of the existing researches simply convert associations of nodes within the snapshot of the evolutionary social network to the weight of edges. However, because of the obvious Matthew effect existing in the interactions of nodes in the real social network, the association strength matrices extracted directly by snapshots are extremely uneven. This paper introduces a new evolutionary social network model. Firstly, we generate probabilistic snapshots of the evolutionary social network data. Afterwards, we use the probabilistic factor model to detect the variation points brought by network events. Finally we partition the network community based on snapshots with stable structures before and after the variation points. According to experimental results, our proposed probabilistic snapshot model is effective for network events detection and network community partition.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Gilbert E, Karahalios K (2009) Predicting tie strength with social media[C]. In: Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (CHI '09). ACM, New York, NY, USA, pp 211–220

  2. Granovetter M (1973) The strength of weak ties[J]. Am J Sociol 78(6):l

    Article  Google Scholar 

  3. Barabási A-L, Bonabeau E (2003) Scale-free networks. Scientific American. vol. 288, no 5, pp 50–59

  4. Scott J, Carrington PJ (2011) The SAGE handbook of social network analysis[M]. SAGE publications

  5. Heiby EM (1995) Chaos theory, nonlinear dynamical models, and psychological assessment[J]. Psychol Assess 7(1):5

    Article  Google Scholar 

  6. Tang L, Liu H (2010) Community detection and mining in social media[J]. Synth Lect Data Min Knowl Disc 2(1):21

    MathSciNet  Google Scholar 

  7. Leskovec J, Horvitz E (2008) Planetary-scale views on a large instant-messaging network. In: Proceedings of the 17th international conference on World Wide Web (WWW '08). ACM, New York, NY, USA, pp 915–924

  8. Jackson MO, Wolinsky A (1996) A strategic model of social and economic networks[J]. J Econ Theory 71(1):44–74

    Article  MathSciNet  MATH  Google Scholar 

  9. Onnela JP, Saramäki J, Hyvönen J et al (2007) Analysis of a large-scale weighted network of one-to-one human communication[J]. New J Phys 9(6):179

    Article  Google Scholar 

  10. Easley D, Kleinberg J (2010) Networks, crowds, and markets[J]. Cambridge Univ Press 6(1):6.1

    MATH  Google Scholar 

  11. Weigend AS, Huberman BA, Rumelhart DE (1990) Predicting the future: a connectionist approach[J]. Int J Neural Syst 1(03):193–209

    Article  Google Scholar 

  12. Kossinets G, Kleinberg J, Watts D (2008) The structure of information pathways in a social communication network. In: Proceedings of the 14th ACM SIGKDD international conference on Knowledge discovery and data mining (KDD '08). ACM, New York, NY, USA, pp 435–443

  13. Goyal A, Bonchi F, Lakshmanan LVS (2010) Learning influence probabilities in social networks. In: Proceedings of the third ACM international conference on Web search and data mining (WSDM '10). ACM, New York, NY, USA, pp 241–250

  14. Mitsudomi T, Morita S, Yatabe Y et al (2010) Gefitinib versus cisplatin plus docetaxel in patients with non-small-cell lung cancer harbouring mutations of the epidermal growth factor receptor (WJTOG3405): an open label, randomised phase 3 trial[J]. Lancet Oncol 11(2):121–128

    Article  Google Scholar 

  15. Zhao-nian Z, Jian-zhong L, Gao H, Shuo Z (2009) Mining frequent subgraph patterns from uncertain graphs. J Softw 20(11):2965–2976

    Article  Google Scholar 

  16. Salakhutdinov R, Mnih A (2007) Probabilistic matrix factorization[C]//21st Annual Conference on Neural Information Processing Systems, NIPS 2007. Vancouver, BC, Canada, pp 1257–1264

  17. Hosmer DW Jr., Lemeshow S (2013) Applied logistic regression. John Wiley & Sons, Inc., Hoboken, New Jersey

  18. Guan N, Wei L, Luo Z, et al (2013) Limited-memory fast gradient descent method for graph regularized nonnegative matrix factorization. PLoS ONE, 8(10), e77162

  19. Rhrissorrakrai K, Gunsalus KC (2011) MINE: module identification in networks[J]. BMC Bioinfo 12(1):192

    Article  Google Scholar 

  20. Abello J, Buchsbaum AL, Westbrook JR (1998) A functional approach to external graph algorithms[M]. Algorithms—ESA’98. Springer, Berlin Heidelberg, pp 332–343

    MATH  Google Scholar 

  21. Capocci A, Servedio VDP, Caldarelli G et al (2004) Communities detection in large networks[M]. Algorithms and Models for the Web-Graph. Springer, Berlin Heidelberg, pp 181–187

    Book  MATH  Google Scholar 

  22. Borgatti SP, Everett MG, Freeman LC (2002) Ucinet for Windows: Software for social network analysis. Harvard, MA: Analytic technologies

  23. McCarney R, Warner J, Iliffe S et al (2007) The Hawthorne effect: a randomised, controlled trial[J]. BMC Med Res Methodol 7(1):30

    Article  Google Scholar 

  24. Kollios G, Potamias M, Terzi E (2013) Clustering large probabilistic graphs[J]. IEEE Trans Knowl Data Eng 25(2):325–336

    Article  Google Scholar 

  25. Shamir R, Sharan R, Tsur D (2004) Cluster graph modification problems[J]. Discret Appl Math 144(1):173–182

    Article  MathSciNet  MATH  Google Scholar 

  26. Nir A, Noa A-E, Edo L, van Zuylen A (2012) Improved approximation algorithms for bipartite correlation clustering. SIAM J Comput 41(5):1110–1121

    Article  MathSciNet  MATH  Google Scholar 

  27. Freire M, Plaisant C, Shneiderman B, et al (2010) ManyNets: an interface for multiple network analysis and visualization. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (CHI '10). ACM, New York, NY, USA, pp 213–222

  28. Keila PS, Skillicorn DB (2005) Structure in the Enron email dataset[J]. Comput Math Organ Theory 11(3):183–199

    Article  MATH  Google Scholar 

  29. Newman MEJ, Girvan M (2004) Finding and evaluating community structure in networks[J]. Phys Rev E 69(2):026113

    Article  Google Scholar 

  30. Shen Y (2013) Detect local communities in networks with an outside rate coefficient[J]. Phys A Stat Mech Appl 392(12):2821–2829

    Article  MathSciNet  Google Scholar 

  31. Hollander M, Wolfe DA, Chicken E (2013) Nonparametric statistical methods. John Wiley & Sons, Inc., Hoboken, New Jersey

  32. Zhao YY, Qin B, Liu T (2010) Sentiment analysis[J]. J Softw 21(8):1834–1848

    Article  Google Scholar 

  33. Jojic O, Shukla M, Bhosarekar N (2011) A probabilistic definition of item similarity. In: Proceedings of the fifth ACM conference on Recommender systems (RecSys '11). ACM, New York, NY, USA, pp 229–236

Download references

Acknowledgments

This research is supported by the Science and Technology Program of Xiamen, China (No.3502Z20153026); Key Program of Science and Technology of Fujian, China (No. 2014H0044, 2015H0037); NSFC (No. 61402387); NSFC (No. 61402390).

Author information

Authors and Affiliations

  1. Software School, Xiamen University, Xiamen, China

    Zhongnan Zhang, Lei Hu, Ming Qiu & Fangyuan Gao

Authors
  1. Zhongnan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lei Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ming Qiu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Fangyuan Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhongnan Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, Z., Hu, L., Qiu, M. et al. Events detection and community partition based on probabilistic snapshot for evolutionary social network. Peer-to-Peer Netw. Appl. 10, 1272–1284 (2017). https://doi.org/10.1007/s12083-016-0427-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12083-016-0427-6

Keywords

Search

Navigation