The dynamics of coupled populations subject to control

Abstract

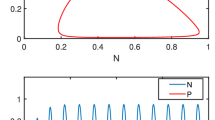
The dynamics of coupled populations have mostly been studied in the context of metapopulation viability with application to, for example, species at risk. However, when considering pests and pathogens, eradication, not persistence, is often the end goal. Humans may intervene to control nuisance populations, resulting in reciprocal interactions between the human and natural systems that can lead to unexpected dynamics. The incidence of these human-natural couplings has been increasing, hastening the need to better understand the emergent properties of such systems in order to predict and manage outbreaks of pests and pathogens. For example, the success of the growing aquaculture industry depends on our ability to manage pathogens and maintain a healthy environment for farmed and wild fish. We developed a model for the dynamics of connected populations subject to control, motivated by sea louse parasites that can disperse among salmon farms. The model includes exponential population growth with a forced decline when populations reach a threshold, representing control interventions. Coupling two populations with equal growth rates resulted in phase locking or synchrony in their dynamics. Populations with different growth rates had different periods of oscillation, leading to quasiperiodic dynamics when coupled. Adding small amounts of stochasticity destabilized quasiperiodic cycles to chaos, while stochasticity was damped for periodic or stable dynamics. Our analysis suggests that strict treatment thresholds, although well intended, can complicate parasite dynamics and hinder control efforts. Synchronizing populations via coordinated management among farms leads to more effective control that is required less frequently. Our model is simple and generally applicable to other systems where dispersal affects the management of pests and pathogens.

Appendices

Appendix A: Solution to ODE

The solutions to Eq. 1 are as follows:

$$\begin{array}{@{}rcl@{}} u(t) &=&\; f_{u}(t, u_{0}, v_{0}) \\ &=& \; c_{1} \; \exp \left[ \frac{r_{uu}+r_{vv}+\alpha}{2} t\right]\\ &&+ c_{2} \; \exp \left[ \frac{r_{uu}+r_{vv}-\alpha}{2} t \right] \end{array} $$

(A.1)

$$\begin{array}{@{}rcl@{}} v(t) &=& \; f_{v}(t, u_{0}, v_{0}) \\ &=& \; c_{1}\; \left( \frac{r_{vv}-r_{uu}+\alpha}{2 r_{uv}} \right) \exp \left[ \frac{r_{uu}+r_{vv}+\alpha}{2} \; t\right]\\ &&+ c_{2}\!\! \; \left( \frac{r_{vv}-r_{uu}-\alpha}{2 r_{uv}} \right) \text{\!exp\!} \left[ \frac{r_{uu}+r_{vv}-\alpha}{2} \; t \right], \end{array} $$

(A.2)

where

$$\begin{array}{@{}rcl@{}} c_{1} &=& \frac{2 r_{uv}v_{0} - u_{0} (r_{vv}-r_{uu}-\alpha)}{2\alpha} \end{array} $$

(A.3)

$$\begin{array}{@{}rcl@{}} c_{2} &=& \frac{u_{0}(\alpha + r_{vv}-r_{uu})-2r_{uv} v_{0}}{2 \alpha} \end{array} $$

(A.4)

$$\begin{array}{@{}rcl@{}} \alpha &=& \sqrt{(r_{uu}-r_{vv})^{2} +4r_{uv}r_{vu}}. \end{array} $$

(A.5)

To get the time of the next treatment given the growth rates and initial conditions, we first rearrange Eqs. A.1–A.2. We denote the time of the next treatment of u and v as T _u and T _v , respectively. The equations for T _u and T _v are the following:

$$\begin{array}{@{}rcl@{}} 2 \alpha N_{\max} &=& \exp \left( \frac{r_{uu}+r_{vv}}{2} T_{u} \right) \left[ \left( \exp \left( \frac{\alpha}{2} T_{u} \right)\right.\right.\\ &&-\left.\exp \left( \frac{-\alpha}{2} T_{u}\right) \right) \left( 2 r_{uv} v_{0} + u_{0} (r_{uu} - r_{vv})\right)\\ &&\quad\left.\!+ u_{0} \; \alpha \left( \exp \left( \frac{\alpha}{2} T_{u}\right) \!+\exp \left( \frac{-\alpha}{2} T_{u}\right) \right) \right] \end{array} $$

(A.6)

$$\begin{array}{@{}rcl@{}} 4 \alpha r_{uv} N_{\max} &=& \exp \left( \frac{r_{uu} + r_{vv}}{2} T_{v} \right) \left[ \left( 2 r_{uv} v_{0} \: (r_{vv}-r_{uu})\right.\right.\\ &&\left.\!+ 4 u_{0} \: r_{vu} r_{uv} \right) \!\left( \exp \left( \frac{\alpha}{2} T_{v} \right)\,-\, \exp \left( \frac{-\alpha}{2} T_{v} \right) \right)\\ &&\left.\!+ 2 r_{uv} v_{0} \alpha\! \left( \exp \left( \frac{\alpha}{2} T_{v} \right) \,+\, \exp \left( \frac{-\alpha}{2} T_{v} \right) \right) \right].\\ \end{array} $$

(A.7)

In Eqs. A.6–A.7, T _u and T _v cannot be solved for explicitly, so we used a numerical root finding algorithm to determine T _u and T _v .

Appendix B: Development of return map

We used the dynamical system described in Eq. 2 to construct a return map that takes the population density u when v is treated and returns u the next time v is treated. We first consider the scenario where u is not treated in between consecutive treatments of v. We denote the time to the next treatment of v as T _v0. In this case, the resulting population density u at the next treatment of v is

$$ \phi (u^{*}) = f_{u} \big(T_{v0}, \; u^{*}, \; N_{\min} \big), $$

(B.1)

where f _u is the solutions to Eq. 1, given in Appendix A. Next, we consider the case where u is treated once in between treatments of v. This leads to a return map of the form,

$$ \phi (u^{*}) = f_{u} \big(T_{v1}, \;N_{\min}, \; f_{v}(T_{u0}, u^{*}, N_{\min}) \big), $$

(B.2)

where T _u0 is the time from the initial treatment of v to the treatment of u and T _v1 is the subsequent time from the treatment of u to the next treatment of v. These two cases can be combined into a single equation as,

$$\begin{array}{@{}rcl@{}} \phi(u^{*}) &=& \underbrace{H(\widetilde{T}_{0})\; f_{u} \big(T_{v0}, \; u^{*}, \; N_{\min} \big)}_{u\text{ not treated}}\\ &&+\! \underbrace{H(\widetilde{T}_{1}) \; \left[1-H(\widetilde{T}_{0})\right]\! \; \!f_{u} \big(T_{v1}, \;N_{\min}, \; f_{v}(T_{u0}, u^{*}, N_{\min}) \big)}_{u\text{ treated once}}.\\ \end{array} $$

(B.3)

We can continue in this way to get the equation that includes the possibility for u being treated twice in between treatments of v,

$$\begin{array}{@{}rcl@{}} \phi(u^{*}) &=& \underbrace{H(\widetilde{T}_{0})\; f_{u} \big(T_{v0}, \; u^{*}, \; N_{\min} \big)}_{u\text{ not treated}} \\ &&+ \underbrace{H(\widetilde{T}_{1}) \; \left[1-H(\widetilde{T}_{0})\right] \; f_{u} \big(T_{v1}, \;N_{\min}, \; f_{v}(T_{u0}, u^{*}, N_{\min}) \big)}_{u\text{ treated once}} \end{array} $$

(B.4)

$$\begin{array}{@{}rcl@{}} &&+ \underbrace{H(\widetilde{T}_{2})\; [1-H(\widetilde{T}_{1})] \; f_{u} \big(T_{v2}, \;N_{\min}, \; f_{v}(T_{u1}, N_{\min}, f_{v}(T_{u0}, u^{*}, N_{\min})) \big)}_{u\text{ treated twice}}. \end{array} $$

By induction, we arrive at the general equation for the return map, given in Eq. 3:

$$\begin{array}{@{}rcl@{}} \phi (u^{*}) &=& \underbrace{\vphantom{\sum\limits_{m=1}^{\infty}} \left[ H(\widetilde{T}_{0}) \right] \; f_{u} \Big(T_{v0}, \: u^{*}, \; N_{\min} \Big)}_{m=0}\\ &&+ \underbrace{\left[ {\sum}_{m=1}^{\infty} H(\widetilde{T}_{m}) \prod\limits_{n=0}^{m-1} [1-H(\widetilde{T}_{n})] \right] f_{u} \Big(T_{vm}, \: N_{\min}, \; v_{m-1} \Big)}_{m \geq 1}.\\ \end{array} $$

(B.5)

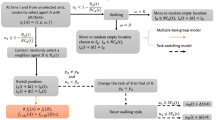
Appendix C: Algorithm describing return map

Because Eqs. A.6–A.7 cannot be solved for T _u and T _v , model analysis by the return map involved simulating successive treatments until v was treated next. The recursive algorithm we applied to calculate the population density u when v was treated next is the following: