Skip to main content
SpringerLink
Log in

Fuzzy clustering algorithm based on modified whale optimization algorithm for automobile insurance fraud detection

  • Special Issue
  • Published:
Evolutionary Intelligence Aims and scope Submit manuscript

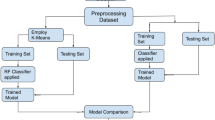
Abstract

Fuzzy c-means (FCM) clustering method is used for performing the task of clustering. This method is the most widely used among various clustering techniques. However, it gets easily stuck in the local optima. whale optimization algorithm (WOA) is a stochastic global optimization algorithm, which is used to find out global optima of a provided dataset. The WOA is further modified to achieve better global optimum. In this paper, a fuzzy clustering method has been proposed by using the strengths of both modified whale optimization algorithm (MWOA) and FCM. The effectiveness of the proposed clustering technique is evaluated by considering some of the well-known existing metrics. The proposed hybrid clustering method based on MWOA is employed as an under sampling method to optimize the cluster centroids in the proposed automobile insurance fraud detection system (AIFDS). In the AIFDS, first the majority sample data set is trimmed by removing the outliers using proposed fuzzy clustering method, and then the modified dataset is undergone with some advanced classifiers such as CATBoost, XGBoost, Random Forest, LightGBM and Decision Tree. The classifiers are evaluated by measuring the performance parameters such as sensitivity, specificity and accuracy. The proposed AIFDS consisting of fuzzy clustering based on MWOA and CATBoost performs better than other compared methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

References

  1. Wang JH, Liao YL, Tsai TM, Hung G (2006) Technology-based financial frauds in Taiwan: issues and approaches. In: IEEE international conference on systems, man and cybernetics, 2006. SMC’06, vol 2. IEEE, pp 1120–1124

  2. Supraja K, Saritha SJ (2017) Robust fuzzy rule based technique to detect frauds in vehicle insurance. In: 2017 International conference on energy, communication, data analytics and soft computing (ICECDS). IEEE, pp 3734–3739

  3. Australia: Insurance (2016) Australia: insurance fraud costs us 1.5 bln annually. http://www.insurancefraud.org/IFNS-detail.htm?key=22516. Accessed 10 Sept 2018

  4. Cutting Corners (2015) Cutting corners to get cheaper motor insurance backfiring on thousands of motorists warns the abi. https://www.insurancefraudbureau.org/media-centre/news/2015/cutting-corners-to-getcheaper-motor-insurance-backfiring-on-thousands-of-motorists-warns-the-abi/. Accessed 10 Sept 2018

  5. Ngai E, Hu Y, Wong Y, Chen Y, Sun X (2011) The application of data mining techniques in financial fraud detection: a classification framework and an academic review of literature. Decis Support Syst 50(3):559–569

    Article  Google Scholar 

  6. Šubelj L, Furlan Š, Bajec M (2011) An expert system for detecting automobile insurance fraud using social network analysis. Expert Syst Appl 38(1):1039–1052

    Article  Google Scholar 

  7. Phua C, Alahakoon D, Lee V (2004) Minority report in fraud detection: classification of skewed data. ACM Sigkdd Explor Newslett 6(1):50–59

    Article  Google Scholar 

  8. Bermúdez L, Pérez JM, Ayuso M, Gómez E, Vázquez FJ (2008) A Bayesian dichotomous model with asymmetric link for fraud in insurance. Insur Math Econ 42(2):779–786

    Article  Google Scholar 

  9. Xu W, Wang S, Zhang D, Yang B (2011) Random rough subspace based neural network ensemble for insurance fraud detection. In: 2011 Fourth international joint conference on computational sciences and optimization (CSO). IEEE, pp 1276–1280

  10. Tao H, Zhixin L, Xiaodong S (2012) Insurance fraud identification research based on fuzzy support vector machine with dual membership. In: 2012 International conference on information management, innovation management and industrial engineering (ICIII), vol 3. IEEE, pp 457–460

  11. Pears R, Finlay J, Connor AM (2014) Synthetic minority over-sampling technique (SMOTE) for predicting software build outcomes. arXiv preprint arXiv:1407.2330

  12. Sundarkumar GG, Ravi V (2015) A novel hybrid undersampling method for mining unbalanced datasets in banking and insurance. Eng Appl Artif Intell 37:368–377

    Article  Google Scholar 

  13. Subudhi S, Panigrahi S (2017) Use of optimized fuzzy c-means clustering and supervised classifiers for automobile insurance fraud detection. J King Saud Univ Comput Inf Sci. https://doi.org/10.1016/j.jksuci.2017.09.010

    Article  Google Scholar 

  14. Lee YJ, Yeh YR, Wang YCF (2013) Anomaly detection via online oversampling principal component analysis. IEEE Trans Knowl Data Eng 25(7):1460–1470

    Article  Google Scholar 

  15. Bezdek JC, Ehrlich R, Full W (1984) FCM: the fuzzy c-means clustering algorithm. Comput Geosci 10(2–3):191–203

    Article  Google Scholar 

  16. Taherdangkoo M, Bagheri MH (2013) A powerful hybrid clustering method based on modified stem cells and fuzzy c-means algorithms. Eng Appl Artif Intell 26(5–6):1493–1502

    Article  Google Scholar 

  17. Esmin AA, Coelho RA, Matwin S (2015) A review on particle swarm optimization algorithm and its variants to clustering high-dimensional data. Artif Intell Rev 44(1):23–45

    Article  Google Scholar 

  18. Ji Z, Xia Y, Sun Q, Cao G (2014) Interval-valued possibilistic fuzzy c-means clustering algorithm. Fuzzy Sets Syst 253:138–156

    Article  MathSciNet  Google Scholar 

  19. Hassanzadeh T, Meybodi MR (2012). A new hybrid approach for data clustering using firefly algorithm and K-means. In: 2012 16th CSI international symposium on artificial intelligence and signal processing (AISP). IEEE, pp 007–011

  20. Niknam T, Firouzi BB, Nayeripour M (2008) An efficient hybrid evolutionary algorithm for cluster analysis. World Appl Sci J 4:300–307

    Google Scholar 

  21. Kao YT, Zahara E, Kao IW (2008) A hybridized approach to data clustering. Expert Syst Appl 34(3):1754–1762

    Article  Google Scholar 

  22. Murthy CA, Chowdhury N (1996) In search of optimal clusters using genetic algorithms. Pattern Recogn Lett 17(8):825–832

    Article  Google Scholar 

  23. Bandyopadhyay S, Maulik U (2002) An evolutionary technique based on K-means algorithm for optimal clustering in RN. Inf Sci 146(1–4):221–237

    Article  Google Scholar 

  24. Alswaitti M, Albughdadi M, Isa NAM (2018) Density-based particle swarm optimization algorithm for data clustering. Expert Syst Appl 91:170–186

    Article  Google Scholar 

  25. Majhi SK, Biswal S (2018) Optimal cluster analysis using hybrid K-Means and Ant Lion Optimizer. Karbala Int J Mod Sci 4(4):347–360

    Article  Google Scholar 

  26. Majhi SK, Bhatachharya S, Pradhan R, Biswal S (2019) Fuzzy clustering using salp swarm algorithm for automobile insurance fraud detection. J Intell Fuzzy Syst 36(3):2333–2344

    Article  Google Scholar 

  27. Pandey AC, Rajpoot DS (2019) Spam review detection using spiral cuckoo search clustering method. Evolut Intell 12(2):147–164

    Article  Google Scholar 

  28. Benmessahel I, Xie K, Chellal M, Semong T (2019) A new evolutionary neural networks based on intrusion detection systems using locust swarm optimization. Evolut Intell 12(2):131–146

    Article  Google Scholar 

  29. Dunn JC (1973) A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters. J Cybern 3(3):32–57. https://doi.org/10.1080/01969727308546046

    Article  MathSciNet  MATH  Google Scholar 

  30. Bezdek JC (1981) Objective function clustering. In: Bezdek James C (ed) Pattern recognition with fuzzy objective function algorithms. Springer, Boston, pp 43–93

    Chapter  Google Scholar 

  31. Mirjalili S, Lewis A (2016) The whale optimization algorithm. Adv Eng Softw 95:51–67

    Article  Google Scholar 

  32. Dua D, Graff C (2019) UCI machine learning repository. School of Information and Computer Science, University of California, Irvine, CA. http://archive.ics.uci.edu/ml

  33. Chen S, Xu Z, Tang Y (2014) A hybrid clustering algorithm based on fuzzy c-means and improved particle swarm optimization. Arab J Sci Eng 39(12):8875–8887

    Article  MathSciNet  Google Scholar 

  34. Friedman M (1937) The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J Am Stat Assoc 32(200):675–701

    Article  Google Scholar 

  35. Friedman M (1940) A comparison of alternative tests of significance for the problem of m rankings. Ann Math Stat 11(1):86–92

    Article  MathSciNet  Google Scholar 

  36. Holm S (1979) A simple sequentially rejective multiple test procedure. Scand J Stat 6:65–70

    MathSciNet  MATH  Google Scholar 

  37. Ke G, Meng Q, Finley T, Wang T, Chen W, Ma W, Ye Q, Liu TY (2017) Lightgbm: a highly efficient gradient boosting decision tree. In: Advances in neural information processing systems, pp 3146–3154

  38. Swain PH, Hauska H (1977) The decision tree classifier: design and potential. IEEE Trans Geosci Electron 15(3):142–147

    Article  Google Scholar 

  39. Dorogush AV, Ershov V, Gulin A (2018) CatBoost: gradient boosting with categorical features support. arXiv preprint arXiv:1810.11363

  40. Breiman L (2001) Random Forests. Mach Learn 45(1):5–32

    Article  Google Scholar 

  41. Chen T, Guestrin C (2016) Xgboost: a scalable tree boosting system. In: Proceedings of the 22nd acmsigkdd international conference on knowledge discovery and data mining. ACM, pp 785–794

  42. Tukey JW (1977) Exploratory data analysis. Addison-Wesley Publishing Company, Reading, MA

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Computer Science and Engineering, Veer Surendra Sai University of Technology, Burla, Odisha, 768018, India

    Santosh Kumar Majhi

Authors
  1. Santosh Kumar Majhi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Santosh Kumar Majhi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Majhi, S.K. Fuzzy clustering algorithm based on modified whale optimization algorithm for automobile insurance fraud detection. Evol. Intel. 14, 35–46 (2021). https://doi.org/10.1007/s12065-019-00260-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12065-019-00260-3

Keywords

Search

Navigation