Skip to main content

Advertisement

SpringerLink
Log in

Seasonal transmission dynamics of measles in China

  • Original Article
  • Published:
Theory in Biosciences Aims and scope Submit manuscript

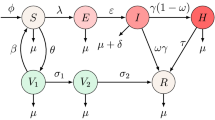
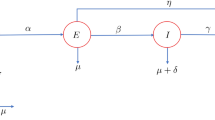
Abstract

Measles, a highly contagious infection caused by the measles virus, is a major public health problem in China. The reported measles cases decreased dramatically from 2004 to 2012 due to the mandatory measles vaccine program started in 2005 and the goal of eliminating measles by 2012. However, after reaching its lowest level in 2012, measles has resurged again since 2013. Since the monthly data of measles cases exhibit a seasonally fluctuating pattern, based on the measles model in Earn et al. (Science 287:667–670, 2000), we propose a susceptible, exposed, infectious, and recovered model with periodic transmission rate to investigate the seasonal measles epidemics and the effect of vaccination. We calculate the basic reproduction number \({\mathcal {R}}_{0}\), analyze the dynamical behavior of the model, and use the model to simulate the monthly data of measles cases reported in China. We also carry out some sensitivity analysis of \({\mathcal {R}}_{0}\) in the terms of various model parameters which shows that measles can be controlled and eventually eradicated by increasing the immunization rate, improving the effective vaccine management, and enhancing the awareness of people about measles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Anderson RM, May RM (1983) Vaccination against rubella and measles: quantitative investigations of different policies. J Hyg Camb 90:259–325

    Article  CAS  Google Scholar 

  • Anderson RM, May RM (1991) Infectious diseases of humans: dynamics and control. Oxford University Press, Oxford

    Google Scholar 

  • Bacaër N, Guernaoui S (2006) The epidemic threshold of vector-borne diseases with seasonality. J Math Biol 53:421–436

    Article  Google Scholar 

  • Bai Z, Liu D (2015) Modeling seasonal measles transmission in China. Commun Nonlinear Sci Numer Simul 25:19–26

    Article  Google Scholar 

  • Bartlett MS (1957) Measles periodicity and community size. J R Stat Soc A 120:48–70

    Article  Google Scholar 

  • Bartlett MS (1960) The critical community size for measles in the U.S. J R Stat Soc A 123:37–44

    Article  Google Scholar 

  • Bolker BM, Grenfell BT (1993) Chaos and biological complexity in measles dynamics. Proc R Soc Lond B 251:75–81

    Article  CAS  Google Scholar 

  • Bolker BM, Grenfell BT (1996) Impact of vaccination on the spatial correlation and persistence of measles dynamics. Proc Natl Acad Sci USA 93:12648–12653

    Article  CAS  Google Scholar 

  • Chinese Center for Disease Control and Prevention (2017) Measles. http://www.chinacdc.cn/jkzt/crb/mz/

  • Conlan AJK, Grenfell BT (2007) Seasonality and the persistence and invasion of measles. Proc R Soc B 274:1133–1141

    Article  Google Scholar 

  • Dietz K (1976) The incidence of infectious diseases under the influence of seasonal fluctuations. In: Berger J et al (eds) Mathematical models in medicine, lecture notes biomathematics, vol 11. Springer, New York, pp 1–11

    Google Scholar 

  • Earn DJD, Rohani P, Bolker BM, Grenfell BT (2000) A simple model for complex dynamical transitions in epidemics. Science 287:667–670

    Article  CAS  Google Scholar 

  • Ferguson NM, Nokes DJ, Anderson RM (1996) Dynamical complexity in age-structured models of the transmission of the measles virus: epidemiological implications at high levels of vaccine uptake. Math Biosci 138:101–130

    Article  CAS  Google Scholar 

  • Ferrari MJ, Grais RF, Bharti N et al (2008) The dynamics of measles in sub-Saharan Africa. Nature 451:679–684

    Article  CAS  Google Scholar 

  • Greenhalgh D (1988) Threshold and stability results for an epidemic model with an age-structured meeting rate. IMA J Math Appl Med Biol 5:81–100

    Article  CAS  Google Scholar 

  • Hamer WH (1906) Epidemic disease in England—the evidence of variability and of persistency of type, the Milroy Lectures III. Lancet 167(4307):733–739

    Article  Google Scholar 

  • Hethcote HW (1983) Measles and rubella in the United States. Am J Epidemiol 117:2–13

    Article  CAS  Google Scholar 

  • Hethcote HW (1988) Optimal ages for vaccination for measles. Math Biosci 89:29–52

    Article  Google Scholar 

  • Keeling MJ, Grenfell BT (1997) Disease extinction and community size: modeling the persistence of measles. Science 275:65–67

    Article  CAS  Google Scholar 

  • London WP, Yorke JA (1973) Recurrent outbreaks of measles, chickenpox and mumps I: seasonal variation in contact rates. Am J Epidemiol 98:453–468

    Article  CAS  Google Scholar 

  • Ma C, An Z, Hao L, Cairns KL, Zhang Y (2011) Progress toward measles elimination in the People’s Republic of China, 2000–2009. J Infect Dis 204:S447–S454

    Article  Google Scholar 

  • Ma C, Hao L, Zhang Y, Su Q, Rodewald L (2014) Monitoring progress towards the elimination of measles in China: an analysis of measles surveillance data. Bull World Health Organ 92:340–347

    Article  Google Scholar 

  • McLean AR, Anderson RM (1988) Measles in developing countries. Part II. The predicted impact of mass vaccination. Epidemiol Inf 100:419–442

    Article  CAS  Google Scholar 

  • National Bureau of Statistics of China (2016) China Demographic Yearbook of 2016. http://www.stats.gov.cn/tjsj/ndsj/2016/indexch.htm

  • National Health and Family Planning Commission of PRC (2017) Bulletins, http://www.nhfpc.gov.cn/jkj/pqt/new_list.shtml

  • Pang L, Ruan S, Liu S, Zhao Z, Zhang X (2015) Transmission dynamics and optimal control of measles epidemics. Appl Math Comput 256:131–147

    Google Scholar 

  • Perko L (2001) Differential equations and dynamical systems, 3rd edn. Springer, New York

    Book  Google Scholar 

  • Perry RT, Gacic-Dobo M, Dabbagh A, Mulders MN, Strebel PM, Okwo-Bele JM (2014) Global control and regional elimination of measles, 2000–2012. MMWR Morb Mortal Wkly Rep 63:103–107

    PubMed  PubMed Central  Google Scholar 

  • Schenzle D (1984) An age-structured model of pre- and pose-vaccination measles transmission. Math Med Biol 1:169–191

    Article  CAS  Google Scholar 

  • Smith H, Waltman P (1995) The theory of the chemostat. Cambridge University Press, Cambridge

    Book  Google Scholar 

  • Soper HE (1929) The interpretation of periodicity in disease prevalence. J R Stat Soc 92(1):34–73

    Article  Google Scholar 

  • Thieme H (1992) Convergence results and a Poincaré–Bendixson trichotomy for asymptotically autonomous differential equations. J Math Biol 30:755–763

    Article  Google Scholar 

  • Tudor DW (1985) An age-dependent epidemic model with application to measles. Math Biosci 73:131–147

    Article  Google Scholar 

  • Wang W, Zhao X-Q (2008) Threshold dynamics for compartmental epidemic models in periodic environments. J Dyn Differ Equ 20:699–717

    Article  Google Scholar 

  • Wang L, Zeng G, Lee LA, Yang Z, Yu J (2003) Progress in accelerated measles control in the People’s Republic of China, 1991–2000. J Infect Dis 187:S252–S257

    Article  Google Scholar 

  • World Health Organization (2009) Progress towards the 2012 measles elimination goal in WHO’s Western Pacific Region, 1990–2008. Wkly Epidemiol Rec 84:271–279

  • World Health Organization (2017) Measles, WHO Fact sheet No. 286, Updated March 2017.http://www.who.int/mediacentre/factsheets/fs286/en/

  • Yang W, Wen L, Li S-L, Chen K, Zhang W-Y, Shaman J (2017) Geospatial characteristics of measles transmission in China during 2005–2014. PLoS Comput Biol 13(4):e1005474. https://doi.org/10.1371/journal.pcbi.1005474

    Article  CAS  PubMed  PubMed Central  Google Scholar 

  • Yorke JA, London WP (1973) Recurrent outbreaks of measles, chickenpox and mumps II: systematic differences in contact rates and stochastic effects. Am J Epidemiol 98:469–482

    Article  CAS  Google Scholar 

  • Zhang F, Zhao X (2007) A periodic epidemic model in a patchy environment. J Math Anal Appl 325:496–516

    Article  Google Scholar 

  • Zhang J, Jin Z, Sun GQ, Sun XD, Ruan S (2012) Modeling seasonal rabies epidemics in China. Bull Math Biol 74:1226–1251

    Article  Google Scholar 

  • Zhao X-Q (2007) Dynamical systems in population biology. Springer, New York

    Google Scholar 

  • Zheng X, Zhang N, Zhang X, Hao L, Su Q et al (2016) Investigation of a measles outbreak in China to identify gaps in vaccination coverage, routes of transmission, and interventions. PLoS ONE 11(12):e0168222. https://doi.org/10.1371/journal.pone.0168222

    Article  PubMed  PubMed Central  Google Scholar 

Download references

Acknowledgements

Research was partially supported by the National Natural Science Foundation of China (Nos. 11471133, 11771168, 11871235) and National Science Foundation (No. DMS-1412454).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Central China Normal University, Wuhan, 430079, People’s Republic of China

    Jicai Huang, Xiao Wu & Xuelei Zhou

  2. Department of Mathematics, University of Miami, Coral Gables, FL, 33146, USA

    Shigui Ruan

Authors
  1. Jicai Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shigui Ruan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiao Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Xuelei Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shigui Ruan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, J., Ruan, S., Wu, X. et al. Seasonal transmission dynamics of measles in China. Theory Biosci. 137, 185–195 (2018). https://doi.org/10.1007/s12064-018-0271-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12064-018-0271-8

Keywords

Search

Navigation