Gresilient supplier selection through Fuzzy Ordinal Priority Approach: decision-making in post-COVID era

Abstract

Because of the COVID-19 outbreak, the supply of both essential and non-essential goods and services has been unprecedentedly disrupted. In the absence of any playbook, the need for innovative technologies to aid recovery from the Supply Chain (SC) disruptions quickly and effectively becomes persistent. The study aims to develop an innovative decision-making technology to handle the supplier selection problems arising from the frequent impreciseness and incompleteness in the nowadays' SC reports within the framework of the gresilient supply chain management. Through the integration of green and resilience aspects of the SCs, the supply chain 'gresilience' has been conceptualized. In light of this construct and based on the data collected from a manufacturing firm, the study deploys a two-fold decomposition of the core algorithm of the Ordinal Priority Approach (OPA), one for attributes and other for alternatives. It extends the OPA to the Fuzzy OPA (OPA-F) for solving the supplier selection problems. The study illustrates how green and resilience aspects of the SC can be integrated to better understand the gresilient suppliers in the wake of the SC disruptions. A novel construct of SC Gresilience is also furnished along with a novel definition of SC Gresilience. It also provides an innovative SC decision-making technology to help procurement managers to evaluate their suppliers. The resultant framework can help them better prepare for the COVID-19 like disruptions in the future.

1 Introduction

Management of supply chains (SCM) is a critical part of human activities for ages. With time, with the emergence of new challenges (e.g., trade and technology wars, unilateralism and trade protectionism, global warming, and infectious diseases) and opportunities (e.g., automation, artificial intelligence, virtual reality, additive manufacturing, big data, blockchain technology, 5G), supply chains are evolving too, and thus new ways to look old activities is getting exceeding importance. Especially since the novel coronavirus (COVID-19) outbreak has severely disrupted global supply chain network and has devastatingly hit almost every industry in the world (Chowdhury et al. 2020), the traditional supply chains have begun looking around to improve sustainability and resilience. It has given rise to "a unique amalgamative failure of economics, healthcare, and society" (Sinha and Paterson 2020) and has substantially impacted the configuration and management of operations and supply chains (Barbieri et al. 2020). As a result of the pandemic, the preferences of customers and buyers have seen unprecedented changes in eating habits, shopping behavior, delivery services, work, and schooling (Thorbecke 2020; Abesamis 2020; Li and Lalani 2020; BM 2020). For instance, in April 2020, Apple CEO Tim Cook said, [Apple's] store traffic [in China] is obviously up from where it was in February, but it is not back to where it was pre the lockdown. There has been, however, more move to online (Gil 2020). While discussing the lasting impact of the pandemic on education, Li and Lalani (2020) argued that the changes coronavirus has caused might be here to stay. On one side, to one industry (e.g., online retailing) the pandemic appeared as a blessing in disguise while, on the other side, it has further accelerated the demise of traditional and inflexible industries and supply chains. Thus, a supply chain crisis is undergoing. 'Survival of the fittest' is the underline message that has been transmitted by the pandemic across the industries. The earlier, the businesses and their supply chains would intercept this message, the earlier they would step in the era of Gresilient supply chain management.

The works of B. Fahimnia played an important role in marrying resilience and sustainability aspects of supply chains (see, e.g., Fahimnia and Jabbarzadeh 2016). Even though the notions like "greenly resilient supply chain" has found its mention in his works (see, e.g., Fahimnia et al. 2018), to the best of our knowledge, the first formal attempt to integrate the green and resilient aspects of supply chains can be attributed to Mohammed (2020), who has recently proposed a preliminary framework of gresilient supply chain management and coined the term 'gresilient'. His study observed that handling supplier selection problems while considering green and resilience aspects, bifurcately, is a dominant tendency in literature. One can add to it that not only in the literature but in practice as well, this bifurcation of green and resilience aspects of the supply chain is very obvious.

If cost, quality, and delivery are regarded as the traditional metrics of supply value chain designs, resilience can be regarded as one of the metrics for future supply chain designs (Betti and Ni 2020). Behzadi et al. (2020) have defined resilience as the ability to recover quickly and effectively from disruption and recognized its critical importance for supply chains. In the COVID-19 era, the Chinese suppliers turned out to be more resilient, in terms of speed and level of recovery, as compared to their counterparts abroad, and thus not only they prevented the loss of performance during the recovery from prolonging but also became a source of hope for the rebuilding of global supply chain resilience (Accenture 2020; Betti and Ni 2020; Gao 2020). Linton and Vakil (2020) also emphasized the need for resilient supply chains in order to avoid the COVID-19 like disruptions in future. In fact, the terms like "Pandemic I" itself demonstrates that the disruptions in future from another pandemic is not beyond question (see, Javed et al. 2020a). Nevertheless, how a resilient supply chain looks like? A resilient supply chain must be able to detect early warning signs of disruption, and it must respond by shifting production to alternative sources. It must have either a diversified supply base or some contingency plan to utilize backup suppliers, as noted by Professor Goker Aydin in Parsons (2020).

To minimize supply chain risks, building resilience in supply chains has long been advocated however the COVID-19 pandemic has proved that even the best combinations of traditional strategies are far away from perfection (Majumdar et al. 2020). Therefore, experimenting with new combinations should be sought in quest to achieve perfection, and better management of pandemic and its consequences. Further, alongside building resilient businesses, a stronger commitment to sustainability goals has also been recognized as an important factor aiding the businesses and their supply chains to better prepare for future disruptions (BM 2020). Although cost reductions and additional value to buyers are commonly mentioned objectives of supply chain management, these objectives have evolved with time to consider sustainable development (Osiro et al. 2018). However, unlike resilience metrics, the metrics of sustainable and green supply chains involve much uncertainty because of the higher degree of subjectivity involved. For example, Ahi and Searcy (2015) identified 2555 unique metrics, showing a lack of agreement on the performance evaluation of green and sustainable supply chain management. It was also recognized that green supply chain management and sustainable supply chain management may not completely overlap, but they were interchangeable in many cases (Ahi and Searcy 2015). However, the current study views green supply chain management (GSCM) as a special case of sustainable supply chain management. This view is consistent with that of Ahi and Searcy (2013). A green supply chain (SC) involves assessment of the environmental performance of the suppliers, requiring them to minimize the environmental impacts of their products throughout its entire life cycle, and evaluating the cost of waste in their operations (Darnall et al. 2008; Beamon 1999). Thus, a green SC can also be viewed as an environmentally sustainable SC (Fahimnia and Jabbarzadeh 2016), as shown in Table 1. Regulatory realm plays an important role in the promotion of green SCM (Zhu et al. 2017) even though over time end-customers' preferences, values and affinity towards green processes and the concerns like global warming, differentiation, reputation are also influencing the adoption of green SCM (Khan and Yu 2019: pp. 20; Kirchoff et al. 2016). Despite a surge in interest towards green and sustainable supply chains in the literature, only a small number of firms can transform environmental investments into sources of competitive advantage (Laari et al. 2018). Considering supply chain resilience, a source of competitive advantage (Wong et al. 2019; Yu et al. 2019; Ribeiro and Barbosa-Povoa 2018; Rajesh 2018) and recognizing the sensitivity of green supply chains to disruptions (Fahimnia et al. 2018), the integration of green aspect of supply chains into the resilience aspect of the supply chain can amount to greater long-term SC performance. Thus, the concept of gresilient supply chains is more likely to outperform traditional supply chains on long-term performance measures (see the definition of Gresilience in Table 1).

Table 1 Three aspects of the supply chain and their conceptualization

Table 2 Transformation of linguistic variables (importance) for alternatives to TFN

Table 3 Transformation of linguistic variables (rating) for attributes to TFN

Table 4 Comparison of the proposed method with some other fuzzy MADM methods

The COVID-19 pandemic has unprecedentedly disrupted the supply chains (SCs) across the world and has provided an opportunity to test the resilience of both traditional and green suppliers. The resulting SC disruptions have led to shortages in the supply of not only medical, biological and healthcare products and services but also of food, beverages, cleaning and sanitizing products, cosmetics, leisure services, electronic products and schooling among others. The flow of both essential and non-essential goods and services has been severely affected. In the absence of any rulebook to cope with the disruptions of this scale and scope, the need for novel and innovative technologies to aid recovery from the SC disruptions quickly and effectively becomes more pressing than ever. Appropriate selection of suppliers is crucial for business success and can help avoid the disruptions like COVID-19 in the future if the sourcing is appropriately done in light of the right criteria and through the right approach. The supplier selection problem is a fundamental problem in the supply chain management literature and has been recognized as an unstructured decision problem requiring multiple criteria decision-making (MCDM) approach to handle it (see, e.g., Weber and Ellram 1993; Mohanty and Deshmukh 1993; Dickson 1966). An improper supplier not only dissatisfies its buyer(s) but also hurts its financial performance and restricts the supply chain surplus from being maximized (Tao et al. 2021). Dickson (1966) and his contemporaries played an important role in formalizing the vendor selection problem. To date, many MCDM methods have been used to solve the supplier selection methods, e.g., Analytic Hierarchy Process (Nydick and Hill 1992), Best Worst Method (Rezaei et al. 2016), VIKOR (Akman 2015), Grey Relational Analysis (Diba and Xie 2019), TOPSIS (Kamalakannan et al. 2020), among others. Multiple attribute decision-making (MADM), sometimes also referred to as discrete multiple criteria decision-making (Guo and Zhao 2017), is a critical system to help decision-makers choose the right alternative from all alternatives available in the light of different conflicting attributes. As compared to routine decision making, however, decision-making under uncertainty is relatively harder because of the relative difference of complexity of the problems and the increasing number of uncertainties surrounding them (Mahmoudi et al. 2021; Javed and Liu 2018). Researchers have proposed various kinds of methodologies for multiple attribute decision-making under uncertainty; nevertheless, they are not free from shortcomings for various reasons. For instance, Javed, Mahmoudi and Liu (2020b) have identified five causes of uncertainty in multiple attribute decision-making processes; (1) Uncertainty because of human error, (2) Uncertainty surrounding data collection instrument and methodology, (3) Uncertainty surrounding the collected data, (4) Uncertainty surrounding data analysis tool and methodology, and (5) Uncertainty surrounding the interpretation of results. If one looks at all existing MADM methods, there is hardly any single approach that can effectively minimize the effect of these uncertainties on the final output of the MADM techniques. For example, the pairwise comparisons, which are the cornerstone of most MADM methods, are known to affect the inconsistency ratio (Čerňanová et al. 2018; Bryson et al. 1995). Normalization of data with different scales (e.g., dollars versus hours) can lead to loss of information; moreover, different normalization methods can influence results differently and, thus, can produce different final rankings (Palczewski and Sałabun 2019a). Different methods of aggregation of data (e.g., average versus geometric mean) can also influence results and ranks (Lin et al. 2020; Saaty and Vargas 2007). To solve these issues a team of researchers has recently proposed a breakthrough methodology in multiple attribute decision-making (see, Ataei et al. 2020). Their method produced reliable results when compared with that of different MADM methods like the AHP, the BWM, TOPSIS, VIKOR, PROMETHEE, and QUALIFLEX. Their methodology is called the Ordinal Priority Approach (OPA) and is a linear programming based intelligent model that is free from several limitations associated with the theory of MADM for decades. For instance, the OPA does not make use of pairwise comparison matrix, decision-making matrix (no need for numerical input), normalization methods, averaging methods for aggregating the opinions of experts (in group decision making), among others (Ataei et al. 2020).

In real life decisions, one cannot rule out the possibility of linguistic variables. The availability of data in the linguistic form is not the only factor restricting the original OPA's functionality. In fact, when the respondents are unable to decide the order of two decision alternatives or criteria, their confusion would create uncertainty in the decision-making process. Since the OPA's input is ordinal data and not numeric data, the respondents (experts) are supposed to provide their preferences for one alternative (or criteria) over the other, which is not always possible considering the limitedness of ones' knowledge.

In the fields like decision analysis, where human originated information is pervasive, the choice of fuzzy set theory is natural (Dubois 2011). Fuzzy set theory has a long and successful history of dealing with the problems containing uncertainty arising from linguistic variables. Since its introduction in the 1960s (Zadeh 1965), the fuzzy theory has seen many applications in various industries, and researchers have integrated it in several MADM methods to make them more realistic and practical. The development of Fuzzy AHP (Khan et al. 2019; Chang 1996), Fuzzy Best Worst Method (Karimi et al. 2020; Guo and Zhao 2017), Fuzzy PROMETHEE (Liao and Xu 2014; Wang and Wu 2011), Fuzzy QUALIFLEX (Zhang and Xu 2015; Chen et al. 2013), Fuzzy TOPSIS (Palczewski and Sałabun 2019b; Chen 2000) and Fuzzy VIKOR (Ploskas and Papathanasiou 2019; Shemshadi et al. 2011; Chen and Wang 2009) are just a few examples. Considering the limitations of the theory of MADM and the inability of the OPA to handle linguistic information, the OPA for Fuzzy Linguistic Information (OPA-F) has been proposed in the current study, using the decomposition approach. The proposed method represents an intelligent MADM methodology that can handle the linguistic variables represented by fuzzy numbers with many conveniences. The approach is novel and is guided by a persuasive methodology of linear programming with a lower computational cost. The approach is original in two ways. First, it pioneers the decomposition of the original OPA into a two-fold framework. Secondly, it makes the OPA more flexible in terms of its ability to handle linguistic information. Meanwhile, the current study uses the OPA-F to evaluate the Chinese suppliers who experienced the disruptions caused by the COVID-19. These suppliers are evaluated based on their gresilience, the resilience of green (environmentally sustainable) supply chain. In a time of crisis, there is little time left for looking for alternative suppliers; thus, if appropriate supplier selection technologies are used today, the effects of the COVID-19 like disruptions can be minimized in the future. In this sense, the old saying 'prevention is better than cure' is true to date.

The rest of the study is organized as follows. The second section involves the preliminaries associated with the proposed method. Here, first of all, the fuzzy numbers and associated concepts are introduced and defined. Secondly, a brief overview of fuzzy linear programming. The third section introduces the OPA-F and its algorithm containing computational steps. The fourth section contains three examples. The first two examples are a part of pilot testing, including complete and incomplete linguistic data sets, and the third example is a practical case study involving multiple attributes and alternatives. The fifth section concludes the study with essential insights and recommendations.

2 Preliminaries of OPA-F

The current section discusses the crucial concepts, knowledge of which is essential in order to grasp the purpose and usefulness of the OPA-F fully. First of all, the relevant concepts of the fuzzy set theory, which has established itself for its ability to handle linguistic information, have been introduced. Secondly, fuzzy linear programming is briefly discussed. Lastly, the OPA-F is presented along with the definitions of associated variables. Here, it should be noted that the authors are well aware of the pedagogic debate in the multiple criteria decision-making literature, where some scholars distinguish criteria from attributes while emphasizing criteria to be a more general term for attributes (Ataei et al. 2020; Ekel et al. 2019; Ploskas and Papathanasiou 2019) although others do not (see, e.g., Javed et al. 2020b; Mahmoudi et al. 2019b; Rezaei 2016), sometimes deliberately (Guo and Zhao 2017). Nevertheless, the current study recognizes MADM as discrete MCDM, i.e., a form of MCDM involving discrete (non-continuous) decision variables (Guo and Zhao 2017), and identifies attributes as the characteristics, qualities, or performance parameters of alternatives (Ekel et al. 2019: pp. 13).

2.1 Fuzzy numbers

Fuzzy numbers are the basic building blocks of the fuzzy set theory, which was proposed by Zadeh (1965). A fuzzy number is a number that is characterized by a possibility distribution or, in other words, is a fuzzy subset of the real number set (Zadeh 1983). Some important definitions associated with the theory of fuzzy numbers are presented below:

Definition 1  The fuzzy number.

Let  ${\tilde{q}} \in F(R)$ be a fuzzy number if:

(1) there exists ${x}_{0} \in R$ such that ${\mu }\space_{\tilde{q}}\left({x}_{0}\right)=1$;

(2) for any ${\alpha }\in [0, 1], \ {\tilde{q}}_{\alpha }=[x,{\mu }_{{\ \tilde{q}}_{\alpha }}(x)\ge \alpha ]$ is a closed interval.

Here R is the set of real numbers, and $F(R)$ represents a family of fuzzy sets defined over R (Guo and Zhao 2017).

Definition 2 The trapezoidal fuzzy number.

A trapezoidal fuzzy number (TrFN) is represented as $\tilde{q} \ =(l, m, n,u)$ with membership function as Eq. (1).

$$\mu \left(x\right)=\begin{cases} \frac{x-l}{m-l}, \space\space \ l \leq x< m \\ 1, \space\space\space \ m \leq x < n \\ \frac{n-x}{u-n}, \space\space \ l \leq x \leq u \end{cases}$$

(1)

where the closed interval $[m, n]$, $l$, and $u$ are the mode, lower and upper limits of $\stackrel\sim{q}$, respectively, whereas $\mu \left(x\right)=0$ if $x<l$ or $x>u$ (Dong and Wan 2018; Pedrycz and Gomide 2007: pp. 36).

Definition 3 The triangular fuzzy number.

A triangular fuzzy number (TFN) is a special case of trapezoidal fuzzy number (TrFN) as a TrFN $\tilde{q} \ =(l, m, n,u)$ becomes TFN $\tilde{q}\space=(l, m, u)$ if $m=n$ (Nasseri et al. 2019: pp. 26; Dong and Wan 2018), i.e., a fuzzy number $\tilde{q}$ on R is called the triangular fuzzy number if its membership function ${\mu }_{\space\stackrel{\sim }{q}}\left(x\right): R\to [0, 1]$ is given by Eq.(2) (Guo and Zhao 2017; Pedrycz and Gomide 2007: pp. 34),

$${\mu }_{\tilde{q}}\left(x\right)=\left\{\begin{array}{c}\frac{x-l}{m-l}, \space\space l\le x<m \\ \frac{u-x}{u-m},\space\space m\le x\le u\end{array}\right.$$

(2)

where ${\mu }_{\ \tilde{q}}\left(x\right)=0$ if $x<l$ or $x>u$.

Since TrFN permits two parameters to represent the possible values (while TFN uses only one) TrFN has stronger ability to capture the fuzziness and uncertainty as compared to TFN (Dong and Wan 2018); however, the trapezoidal membership function leads to the violation of $\otimes$-transitivity: $\upmu \left(\mathrm{x},\mathrm{ z}\right)\ge \mathrm{max}\{0,\upmu \left(\mathrm{x},\mathrm{y}\right)+\upmu \left(\mathrm{y},\mathrm{z}\right)-1\}$, which is one of the weakest forms of transitivity (Kundu 1999). On the other hand, the TFN has seen many applications perhaps because of its striking simplicity (that are eventually exploitable in further steps of processing) and reasonably limited availability of the pertinent information about the linguistic terms (Pedrycz 1994). Under some weak assumptions, triangular membership functions can comply with the relevant optimization criteria, thus providing fundamental reasons legitimizing the use of the triangular membership functions (Pedrycz 1994). Thus, replacing TrFN with TFN is an acceptable and legitimate approach in literature not only for the sake of convenience but also for some fundamental reasons (see, e.g., Kundu 1999; Pedrycz 1994). Also, TFN can furnish a very flexible approach to handle linguistic variables, e.g., see Tables 2 and 3 and Figs. 1 to 2.

In light of the objectives of the current study, the transformation of linguistic variables to TFN, and the associated OPA-F ranks (r), are presented in Tables 2 and 3. The scaling is the reverse of the scale one finds in Chen (2000) and Ploskas and Papathanasiou (2019) making it consistent with the OPA paradigm of scaling. Here it should be noted that in the OPA-F, to transform linguistic variables to TFN, it is suggested to use a number close to zero (e.g., 0.01) instead of absolute zero to prevent the disappearance of constraint resulting from the multiplication with zero.

Definition 4  The athematic operations of two triangular fuzzy numbers.

Assume that $\tilde{A}\space=\left[l,m,u\right]$ and $\tilde{B}\space=\left[{l}^{{^{\prime}}},{m}^{{^{\prime}}},{u}^{{^{\prime}}}\right]$ are two positive triangular fuzzy numbers/sets. The standard approximate athematic operations of these two fuzzy numbers are defined as Eqs. (3) to (4) (Giachetti and Young 1997).

$$\tilde{A}+\tilde{B} \ =\left[l+{l}^{{^{\prime}}},m+{m}^{{^{\prime}}},u+{u}^{{^{\prime}}}\right]$$

(3)

$$\tilde{A}-\tilde{B} \ =\left[l-{u}^{{^{\prime}}},m-{m}^{{^{\prime}}},u-{l}^{{^{\prime}}}\right]$$

(4)

$$\tilde{A}\times \tilde{B} \ =\left[l.{l}^{^{\prime}},m.{m}^{^{\prime}},u.{u}^{^{\prime}}\right]$$

(5)

$$\tilde{A}/\tilde{B} \ =\left[l/{u}^{^{\prime}},m/{m}^{^{\prime}},u/{l}^{^{\prime}}\right]$$

(6)

Since TFNs are not closed under any given extended fuzzy operation, the resulting fuzzy number can be calculated using approximate methods (Seresht and Fayek 2019; Guerra and Stefanini 2005; Irion 1998). For the information about the basic operations of fuzzy sets, Zadeh (1965) can be consulted.

Definition 5 Graded Mean Integration Representation of a TFN.

Let the graded mean integration representation (GMIR) $R(\tilde{a})$ of a TFN ${\tilde{a}}$ represent the ranking of a triangular fuzzy number. Let $\tilde{q} \ =({l}_{i},{m}_{i},{u}_{i})$, and the GMIR $R(\tilde{q})$ of a TFN $\tilde{a}$ can be calculated as Eq. (7) (Chen and Hsieh 2000).

$$R\left(\tilde{q}\right)=\frac{{l}_{i}+4{m}_{i}+{u}_{i}}{6}$$

(7)

GMIR can also be defined as Eq. (8) (Kumar et al. 2011).

$$R\left(\tilde{q}\right)=\frac{{l}_{i}+2{m}_{i}+{u}_{i}}{4}$$

(8)

GMIR is also known as the ranking function, usually defined as $R:F(R)\to R$, where $F(R)$ is a set of fuzzy numbers defined on a set of real numbers (Kumar et al. 2011), thus making it an essential measure of defuzzification. The data analysts can choose one of these representations according to their needs and convenience.

2.2 Fuzzy linear programming

Linear Programming (LP) was founded by the Soviet mathematician Leonid Kantorovich in 1939 (see, Kantorovich 1960; Koopmans 1960). Later, G. B. Dantzig and John von Neumann played an important role in familiarizing the West with linear programming. The LP is a mathematical technique for the optimal allocation of scarce resources to several competing activities based on given criteria of optimality (Nasseri et al. 2019: pp. 55). The four essential components of any linear programming model are decision variables, objective function, constraints, and parameters (Nasseri et al. 2019: pp. 40). Most of the LP models available to the decision-makers conventionally involve crispy parameters in objective function and constraints; however, in the real world, one frequently encounters linguistic parameters characterized by impression. When the decision-making environment surrounds impreciseness or uncertainty, linear programming with crispy parameters is not an ideal choice. To solve real-world problems, the researchers have been attempting to extend conventional LP models to uncertain and imprecise environments, such as fuzzy environments. As confirmed by Feylizadeh et al. (2018), the basic idea of fuzzy mathematical programming was first presented by Tanaka et al. (1974); however, Zimmerman (1978) has been credited with making a pioneering attempt in formalizing fuzzy linear programming (FLP). Since then, numerous scholars around the world have dedicated themselves to improving the methodology of FLP.

In linear programming problems, the coefficients of the objective function and constraints are not necessarily crispy. They can be intervals (Oliveira and Antunes 2007) as well as fuzzy (Jimenez et al. 2007; Peng-fei 2004; Fang et al. 1999) or grey (Mahmoudi et al. 2019a, 2020b). Since the fuzziness may appear in a linear programming problem in many ways, the definition of a fuzzy linear programming problem is not unique (Nasseri et al. 2019: pp. 39). Nevertheless, the main objective in fuzzy linear programming is to find the best solution possible with imprecise or vague information whereas imprecision or vagueness in fuzzy linear programming has many sources, e.g., the vagueness in the constraint satisfaction limits, imprecise information of the constraints variables, among others (Kaur and Kumar 2016: pp. 2).

As stressed by Zimmermann (1978), one of the pioneers of fuzzy linear programming, using different ways of combining individual objective functions in order to determine an optimal compromise solution is a realistic approach. The OPA-F is another attempt in this context where fuzziness is both recognized and estimated. However, the issues associated with fuzziness, like the vagueness in constraint satisfaction limits and impreciseness of the constraint variables, have minimal impact on the decision outcomes because the input data is defined by ordinal relations (preferences) instead of absolute values. The following section explains the OPA-F, along with its key characteristics.

A fuzzy model with triangular fuzzy numbers is a well-known approach (see, e.g., Kaur and Kumar 2016: Chapter 5). Let's consider the fuzzy model (9) with the triangular fuzzy numbers $({p}_{j},{q}_{j},{r}_{j})$ $({x}_{j},{y}_{j},{z}_{j})$, $({a}_{ij},{b}_{ij},{c}_{ij})$ and $({b}_{i},{g}_{i},{h}_{i})$.

$$\begin{aligned} Maximize \ (or Minimize) &\Sigma^n_{j=1} (p_{j},q_{j},r_{j}) \otimes(x_{j},y_{j},z_{j}) \\ Subject \ to \sum^n_{j=1}(a_{ij},b_{ij},c_{ij}) &\otimes (x_{j},y_{j},z_{j}) \mathop = \limits_> ^< \ (b_{i},g_{i},h_{i}) \quad \forall_i =1,2, \cdots, m.\end{aligned}$$

(9)

$\left({x}_{j},{y}_{j},{z}_{j}\right)$, $({p}_{j},{q}_{j},{r}_{j})$ and $\left({a}_{ij},{b}_{ij},{c}_{ij}\right)$ are non-negative fuzzy numbers, where,

$${x}_{j}\le {y}_{j}\le {z}_{j}$$

To solve the fuzzy model (9), the current study employs the most straightforward method, which is suitable for the OPA. This approach is inspired by the works of Kumar et al. (2011) and Azar and Toghyani (2014). In fact, all constraints in the model (9) should be converted to equality using fuzzy slack variables (${s}_{i}$, ${t}_{i}$, ${f}_{i}$). It should be noted that it can be negative, positive, or zero based on the situation. Finally, the model (9) can be converted into the crisp model (10).

$$\begin{aligned}&Maximize \ (or \ Minimize) \ R \ (\Sigma^n_{j=1}(p_j, q_j, r_j \otimes (x_j, y_j, z_j)) \\ &\text{Subject to} \\& \sum^n_{j=1} a_{ij}x_{j} + s_i = b_i \quad \forall \ i = 1,2, ..., m. \\ &\sum^n_{j=1} b_{ij} y_j + t = g_i \quad \forall \ i = 1,2, ..., m. \\& \sum^n_{j = 1} c_{ij}z_{j} + f_{i} = h_{i} \quad \forall \ i = 1,2, ..., m.\end{aligned}$$

(10)

$\left({x}_{j},{y}_{j},{z}_{j}\right)$  $({p}_{j},{q}_{j},{r}_{j})$ and $\left({a}_{ij},{b}_{ij},{c}_{ij}\right)$ are non-negative fuzzy numbers, where,

$$\begin{aligned} &x_j \leq y_j \leq z_j ; \\ &s_i \leq t_i \leq f_i \end{aligned}$$

One can solve this model using any standard algorithm or software capable of handling linear programming models.

3 OPA for fuzzy linguistic information (OPA-F)

Conventionally, decision-making is the process of identifying and choosing alternatives based on the values and preferences of the decision-maker (Kaur and Kumar 2016: pp. 7). Therefore, a reliable decision-making technique should facilitate the decision-makers by incorporating their values, as manifested through the decision variables, and the associated preferences. Most popular MADM methods try to evaluate the alternatives based on the attributes' weights, provided by the experts, and the preferences, as manifested through pairwise comparisons. Thus, not only the weights are subjective; instead, the matrix resulting from the pairwise comparisons of the preferences is also prone to inconsistencies, reported by inconsistency ratio.

Determining the weights of criteria from ordinal information remained a topic of interest among scholars for decades. The works of J. Simos is of particular interest in this realm. In 2019, Ataei et al. (2020) proposed the Ordinal Priority Approach (OPA) for multiple attribute decision-making where ordinal information is used to determine weights with the aid of linear programming (LP). Unlike the Simos procedure that allows determining weights of criteria from the preferences of the decision-makers using a set of simplistic mathematical rules, some of which are debatable (Figueira and Roy 2002), the OPA neither demands complex mathematical calculations from its user, nor it involves the calculation of non-normalized and normalized weights. Because of the unique LP-based approach, the problems arising from rounding-off the values and inclusion or exclusion of subsets of weights are also not involved. Even though there exist some techniques, like the UTA algorithms and other ordinal regression methods (Jacquet-Lagreze and Siskos 1982), where one may find the application of LP to handle ordinal information, their dependence on pairwise comparisons make their use inconvenient for a complex problem involving numerous relations. These problems are resolved in the OPA. Further, the most important attribute that distinguishes the OPA among the family of decision-making models is its ability to simultaneously determine the weights of criteria, experts, and alternatives (Mahmoudi et al. 2020a, 2021).

The OPA revisited the decision-making process in a very novel way. In the OPA, decision-making is the process of identifying and choosing alternatives based on the information and preferences of the experts, respectively. Here, the information is characterizations of the alternatives and attributes, while the preferences are of these alternatives and attributes as defined by the experts. Thus, in the OPA paradigm of decision-making, the three crucial elements of the decision-making process are alternatives, attributes, and experts, each defined by ordinal relations. Here, the preferences for attributes define the preferences of alternatives, according to each expert, in the order of priority, without demanding any other information from the experts except these preferences. The OPA resorts to mathematical modelling of multi-attribute decision-making problems with the aid of linear programming to objectively determine the weights and ranks of alternatives, attributes, and experts. The input of the OPA is ordinal data, and the output is crisp numbers. In the OPA, k alternatives are ranked according to the following three stages;

• (i) Ranking of the attributes by each expert,

• (ii) Ranking of the experts based on the organizational hierarchy (authority), experience (seniority), educational background, among others,

• (iii) Ranking of the alternatives by each expert against multiple attributes.

The contributions of the OPA to the multi-attribute decision-making theory can be attributed to its independence over (a) normalization of observations, (b) aggregation operations over input data, (c) pairwise comparisons, (d) fully complete datasets, (e) user-defined (subjective) weights of attributes, (f) cardinal data, etc. Therefore, the simultaneous addressing of multiple constraints co-founded within the theory of MADM is the core theoretical contribution of the OPA and its extension in the form of OPA-F. Further, the method introduces a unique transformation of ordinal information to cardinal weights with minimum loss of information resulting from these constraints. These advantages have made the OPA a potent competitor to the mainstream MADM methods such as shown in Table 4.

Every work, which is a product of human efforts, is incomplete and has certain shortcomings (Javed 2019). This fact creates room for further developments, innovations, and improvements. In the real world, most of the decisions come from subjective ordinal preferences. For example, a customer buying a car sees multiple cars in a showroom, neither prepares a pairwise comparison matrix nor normalizes any data. What he (or she) does is prioritizing all available cars according to the attributes (e.g., speed, price, brand, color, comfort, etc.) in his (or her) mind. A manager employing a supplier from a pool of suppliers would feel more convenient if asked to rank which of the two suppliers are relatively more reliable than if asked to assign numbers to different suppliers in terms of their reliability. A wise teacher would avoid segregating her (or his) students as good or bad but would instead prefer prioritizing them based on given attributes (e.g., class participation, performance in exams, participation in extracurricular activities, etc.). However, even though, in real life, most decisions are guided by relative priorities, one often encounters linguistic variables. "I want a beautiful electric-bike for my daughter," says a customer to the seller. "My product is of very high quality," tells a supplier to a company's manager. "My team has almost finished its work," tells a team leader to her boss. One frequently comes across such phrases in real life. Beautiful, very high and almost are all linguistic variables with fuzzy meanings. There is a chance that the bike father thought was beautiful might not appear beautiful when presented to his daughter. The very high-quality product was, in fact, from the supplier who was new in business (thus, the reliability was low). By almost, the team leader meant that more than 80% of work had been finished while the recipient of the information, the boss, interpreted it as 99%! Linguistic variables, or fuzzy variables, are not only the source of uncertainty in the input (data) but also the source of error in output (e.g., ranking of alternatives). Thus, handling them requires special care.

In contrast to the idea of numeric variables, linguistic variables may assume values consisting of words or sentences expressed in a particular language and thus can be regarded as variables whose values are fuzzy sets (Pedrycz and Gomide 2007: pp. 41). Linguistic variables are efficient and powerful means to denote the qualitative judgments of the decision-makers (Meng et al. 2019). One of the limitations of the original OPA is its inability to handle linguistic information, and the fuzzy set theory provides a promising avenue to overwhelm this limitation . In real-world problems, values of interest are often not measured but are estimated based on the perception and knowledge of a human being thus, natural language-based estimations can be used, which can be formally described by fuzzy numbers (Aliev et al. 2018). In light of this background, it is stated that the OPA-F attempts to transform linguistic information into triangular fuzzy numbers and then uses the OPA's unique approach of linear programming based multi-attribute decision making in the two-fold setting. One can also argue, the underline model of the OPA-F to be a Fuzzy Linear Programming (FLP) with the following defining characteristics:

• (i) Fuzzy numbers in the coefficients of the objective function

• (ii) Fuzzy numbers in the coefficients of the constraints

• (iii) Priorities defined through linguistic variables represented by triangular fuzzy numbers

• (iv) Fuzzy multiple attribute decision making

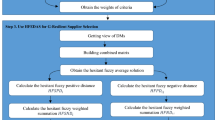
Thus, in short, the OPA-F is one of the points where fuzzy multi-attribute decision-making and fuzzy linear programming meet each other. The flowchart of the OPA-F is shown in Fig. 3.

Fig. 1

Fuzzy membership function for linguistic values for alternatives

Fig. 2

Fuzzy membership function for linguistic values for attributes

Fig. 3

The flow chart of the stages of OPA-F

3.1 The algorithm of OPA-F

Consider the definition of essential sets, indexes, parameters, and variables associated with the OPA-F, as shown in Table 5.

Table 5 Sets, indexes, parameters, and variables of OPA-F

Table 6 The Attributes and their type – Example 1

Table 7 A Hypothetical Supplier Selection Problem – Example 1

Table 8 The fuzzy weights of the three attributes – Example 1

Table 9 Fuzzy score of each supplier against each attribute – Example 1

Equation (11) expresses the rank of alternatives for different values of $i, j$ and $k$. In this equation,${{A}_{ijk}}^{(r)}$ is related to $k$th alternative while it has been opined by expert $i$ and based on attribute $j$ to rank $r$ (Ataei et al. 2020).

$${{A}_{ijk}}^{1}\ge {{A}_{ijk}}^{2}\ge \dots \ge {{A}_{ijk}}^{r}\ge {{A}_{ijk}}^{r+1}\ge \dots \ge {{A}_{ijk}}^{m} \qquad \qquad \qquad \forall i, j, k$$

(11)

Likewise, we have the same relation for the weight of attributes because the experts' opinions for alternatives and attributes are independent.

$${{W}_{ij}}^{1}\ge {{W}_{ij}}^{2}\ge \dots \ge {{W}_{ij}}^{r}{{\ge W}_{ij}}^{r+1}\dots \ge {{W}_{ij}}^{m-1}{{\ge W}_{ij}}^{m} \qquad \qquad \qquad \forall i , j$$

(12)

Based on Eq. (12), the relation(s) between ${{W}_{ij}}^{r}$ and ${{W}_{ij}}^{r+1}$ can be defined as

$$\begin{aligned} W_{ij}^{1}-W_{ij}^{2}\ge 0 , \\ W_{ij}^{2}-W_{ij}^{3}\ge 0 , \\ \dots \\ W_{ij}^{r}-W_{ij}^{r+1}\ge 0 \\ \dots \\ W_{ij}^{m-1}-W_{ij}^{m}\ge 0 \end{aligned}$$

(13)

From Eq. (13), it is evident that the weight of $r$ ^th attribute is superior to that of $(r+1)$ attribute. Now, let us consider the degree of preference in this relationship. Since our input data are linguistic variables, if we multiply both sides of Eq. (13) by linguistic variable ${{a}_{ij}}^{r}$ with rank $r$ to reflect the degree of importance, one gets Eq. (14)

$${{a}_{ij}}^{r}\left({{W}_{ij}}^{r}-{{W}_{ij}}^{r+1}\right)\ge 0 \qquad \qquad \forall \ i , j , r$$

(14)

To find a suitable weight for attributes, the mathematical model (15) should be solved. In this model, we want to maximize the preference of attributes for each expert.

$$\begin{aligned} &Max \left\{{a_{ij}}^{r}\left({W_{ij}}^{r}-{W_{ij}}^{r+1}\right),{a_{ij}}^{m}{W_{ij}}^{m}\right\} \quad \forall \ i, j , r \\ &\mathrm{S.t:} \\ &\sum_{i=1}^{p}\sum_{j=1}^{n}{W_{ij}}=1 \\ &{W_{ij}}\ge 0\qquad \qquad \qquad \forall \ i,j \end{aligned}$$

(15)

Since there are different attributes for each MADM problem, the model (15) is multiple objective and non-linear simultaneously. For solving this model, the minimization objectives would be maximized, which is shown in Eq. (16).

$$\begin{aligned} &\mathrm{Max} \ Min\left\{ {a_{ij}}^{r}\left({W_{ij}}^{r}-{W_{ij}}^{r+1}\right),{a_{ij}}^{m}{W_{ij}}^{m}\right\} \quad \forall \ i, j \ and \ r \\ &\mathrm{S.t:}\\ &\sum_{i=1}^{p}\sum_{j=1}^{n}W_{ij}=1 \\ &W_{ij}\ge 0\qquad \qquad \qquad \forall \ i,j \end{aligned}$$

(16)

It should be noted that solving model (16) is inconvenient; thus, one needs to transform it into a linear model. To handle this issue, we are considering $Z$, as expressed in Eq. (17), and will replace it into the model (16).

$$Z=Min\left\{ {{a}_{ij}}^{r}\left({{W}_{ij}}^{r}-{{W}_{ij}}^{r+1}\right),{{a}_{ij}}^{m}{{W}_{ij}}^{m}\right\}$$

(17)

After substituting Eq. (17) into the model (16), the linear model (18) will be obtained, which can be solved conveniently.

$$\begin{aligned}& \mathrm{Max} \ {Z} \\ &\mathrm{S.t:} \\ &{a_{ij}}^{r} ({W_{ij}}^{r}-{W_{ij}}^{r +1})\ge \mathrm{Z} \quad \forall \ i, j , r \\ &{a_{ij}}^{m}{W_{ij}}^{m}\ge \mathrm{Z } \qquad \qquad \forall \ i, j \\ &\sum_{i=1}^{p}\sum_{j=1}^{n}{W}_{ij}=1 \\ &{W}_{ij}\ge 0 \qquad \qquad \qquad \forall \ i,j \end{aligned}$$

(18)

where Z: Unrestricted in sign.

After solving this model for any MADM problem, one can extract the weights of attributes. Here, it should be noted that by using the same approach, one can have model (19) to calculate a score for alternatives.

$$\begin{aligned} &\mathrm{Max} \ {Z} \\ &\mathrm{S.t:} \\ &{a_{ijk}}^{r}\left({S_{ijk}}^{r}-{S_{ijk}}^{r+1}\right)\ge Z \qquad \forall \ i, j, k, r \\ &{a_{ijk}}^{m}{S_{ijk}}^{m}\ge Z \qquad\qquad \quad \forall \ i, j, k \\ &\sum_{i=1}^{p}\sum_{j=1}^{n}\sum_{k=1}^{m}{S}_{ijk}=1 \\ &{S}_{ijk}\ge 0 \qquad \qquad \quad \forall \ i, j, k \end{aligned}$$

(19)

where Z: Unrestricted in sign.

One may ask why we did not consider the weights of attributes and the scores of the alternatives in one model? Why was the decomposition approach necessary? It should be noted that cracking ordinal data defined through linguistic variables using a composite model like the one in the OPA is a challenging venture. Thus, the decomposition approach was used. Now, let us examine the computational steps of the proposed model. The fuzzy approach is selected to contain imprecision characterized by linguistic information as it has shown suitable performance in many earlier works in similar environments. The algorithm of the OPA-F involves four steps, which are listed below. The first two steps define the two-fold decomposition approach of the OPA-F that shows its two core models, while the rest of the steps involve the efforts directed at selecting an optimum alternative in the fuzzy linguistic environment.

Step 1: Solve the following model, called the Attributes Model of the OPA-F, for calculating the weights of the attributes:

$$\begin{aligned} &\mathrm{Max} \ \tilde{Z}\\ &\mathrm{S.t:} \\ &{\tilde{a}_{ij}}^{r}\left({\tilde{W}_{ij}}^{r}-{\tilde{W}_{ij}}^{r+1}\right)\ge \tilde{Z} \qquad \qquad \forall \ i, j, r \\ &{\tilde{a}_{ij}}^{m} {\tilde{W}_{ij}}^{m}\ge \tilde{Z} \qquad \qquad \qquad \qquad \quad \forall \ i, j \\ &\sum_{i=1}^{p}\sum_{j=1}^{n} \tilde{W}_{ij}=(0.8, 1, 1.2) \\ &{\tilde{l}_{ij}^{w}} \le {\tilde{m}_{ij}^{w}}\le {\tilde{u}_{ij}^{w}} \qquad \qquad \qquad \quad \forall \ i, j \\ &{\tilde{l}_{ij}^{w}}\ge 0 \qquad\qquad \qquad \qquad \quad \forall \ i, j\end{aligned}$$

(20)

Step 2: Solve the following model, called the Alternatives Model of the OPA-F, for calculating the score of the alternatives:

$$\begin{aligned} &\mathrm{Max} \ \tilde{Z} \\ &\mathrm{S.t:} \\ &{\tilde{a}_{ijk}}^{r}\left({\tilde{S}_{ijk}}^{r}-{\tilde{S}_{ijk}}^{r+1}\right)\ge \tilde{Z} \qquad \qquad \forall \ i, \ j, \ k, \ r \\ &{\tilde{a}_{ijk}}^{m} \ {\tilde{S}_{ijk}}^{m}\ge \tilde{Z} \qquad \qquad \qquad \qquad \quad \forall \ i, \ j, \ k \\ &\sum_{i=1}^{p}\sum_{j=1}^{n}\sum_{k=1}^{m}{\tilde{S}}_{ijk}=(0.8, 1, 1.2) \\ &{\tilde{l}}_{ijk}^{S}\le {\tilde{m}}_{ijk}^{S}\le {\tilde{u}}_{ijk}^{S} \qquad \qquad \qquad \qquad \forall \ i, \ j, \ k \\ &{\widehat{l}}_{ijk}^{S}\ge 0\qquad \qquad \qquad \qquad \forall \ i, \ j, \ k \end{aligned}$$

(21)

Step 3: Calculate the Total Fuzzy Score ($\tilde{TS}$) for each alternative by using the following formula:

$${\tilde{TS}}_{k}=\sum_{i=1}^{p}\sum_{j=1}^{n}{\tilde{W}}_{ij}.{\tilde{S}}_{ijk} \qquad \qquad \forall \ k$$

(22)

Step 4: After calculating $\tilde{TS}$ for each alternative, one can calculate the ranking function by using a suitable defuzzification formula such as:

$$R\left({\tilde{TS}}_{k}\right)=\frac{{l}_{k}^{ts}+4{m}_{k}^{ts}+{u}_{k}^{ts}}{6} \qquad \qquad \forall \ k$$

(23)

Later, based on these scores, the alternatives can be ranked. A higher score implies a higher rank, and a lower score means a lower rank.

4 Results

In this section, the proposed model's execution is demonstrated through three examples. The first example is of a hypothetical multi-attribute decision-making problem. The second example is the modification of the first one resulting from a blank space. Thus, if the first example demonstrates the application of the OPA-F on complete datasets, the second example does so on incomplete datasets. The third example is a real-world case study, which demonstrates the proposed model's applicability for handling real-life MADM problems.

4.1 Example 1: the case of complete data

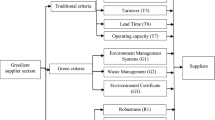
A procurement manager in an electric car manufacturing company received proposals from six suppliers (A1, A2, …, A6) against a tender floated by the company a few weeks back. For him, the important attributes against which he has to prioritize the six available suppliers are Material Safety (C1), Environmental Management Systems (EMS) Certifications (C2), and Pollution (C3). The MADM problem, thus developed, can be represented, as shown in Fig. 4.

Fig. 4

The MADM problem in Example 1

Let us say, when he is asked to record his observations about the six suppliers, he reported that for him, the importance of Material Safety is very high, while that of the Pollution and EMS Certifications are high and medium, respectively. He also made it very clear that except pollution (–), all other attributes are higher-the-better (+), as shown in Table 6. How he rated each supplier in light of these three alternatives is being shown in Table 7. The lower-the-better attribute's direction is reversed, thus it has become pollution control (+).

To find the best supplier from the pool of six suppliers, the study deployed the OPA-F algorithm, as reported  in the previous section. The first step of the algorithm is to estimate the fuzzy weights of the attributes using the Eq. (20).

$$\begin{aligned} &Max \ {Z} \\ &\mathrm{S.t:} \\ &\left(0.01, 0.01, 0.1\right)*\left({\tilde{W}_{1}}-{\tilde{W}_{3}}\right)\ge \ \tilde{Z} \\ &\left(0.01, 0.1, 0.3\right)*\left({\tilde{W}_{3}}-{\tilde{W}_{2}}\right)\ge \ \tilde{Z} \\ &\left(0.3, 0.5, 0.7\right)*\left({\tilde{W}_{2}}\right)\ge \ \tilde{Z} \\ &{\tilde{W}_{1}}+{\tilde{W}_{2}}+{\tilde{W}_{3}}=(0.8, 1, 1.2) \\ &{\tilde{W}_{1}},{\tilde{W}_{2}},{\tilde{W}_{3}}\ge 0 \end{aligned}$$

(24)

After employing the model (10), the fuzzy model (24) can be converted to the crisp model (25).

$$\begin{aligned} &Max \frac{({z_l}+2{z_m}+{z_u})}{4} \\ &\mathrm{S.t:} \\ &0.01 * \left({l_1}-{u_3}\right)-{s_1}={z_l} \\ &0.01 * \left({m_1}-{m_3}\right)-{t_1}={z_m} \\ &0.1 * \left({u_1}-{l_3}\right)-{f_1}={z_u} \\ &0.01 * \left({l_3}-{u_2}\right)-{s_2}={z_l} \\ &0.1 * \left({m_3}-{m_2}\right)-{t_2}={z_m} \\ &0.3 * \left({u_3}-{l_2}\right)-{f_2}={z_u} \\ &0.3 * \left({l_2}\right)-{s_3}={z_l} \\ &0.5 * \left({m_2}\right)-{t_3}={z_m} \\ &0.7 * \left({u_2}\right)-{f_3}={z_u} \\ &{l_1}+{l_2}+{l_3}=0.8 \\ &{m_1}+{m_2}+{m_3}=1 \\ &{u_1}+{u_2}+{u_3}=1.2 \\ &{l_1}\le {m_1}\le {u_1}; \ {l_2}\le {m_2}\le {u_2}; \ {l_3}\le {m_3}\le {u_3} \\ &{s_1} \le {t_1}\le {f_1};\ {s_2}\le {t_2}\le {f_2};\ {s_3}\le {t_3}\le {f_3} \\ &{l_1}\ge 0; \ {l_2}\ge 0; \ {l_3}\ge 0; \ {s_1}\ge 0; \ {s_2}\ge 0; \ {s_3}\ge 0; \ {z_l}\ge 0 \end{aligned}$$

(25)

The results are shown in Table 8. Here, L, M, and U represent the lower, medium, and upper bounds of the weights denoted by the triangular fuzzy number. If one desires, these attributes can be ranked, e.g., in the present case, the weight of Material Safety is highest, and the weight of EMS Certifications is least while the weight of the Pollution is in between them, i.e., C1 > C3 > C2. It should be noted that the weights of attributes, as reported in Table 8, are obtained after solving the model (25).

The next step of the algorithm is to estimate the fuzzy score of each supplier against each attribute using the Eq. (21).

$$\begin{aligned}& \mathrm{Max} \ \tilde{Z}\\ &\mathrm{S.t:} \\ &\left(0.01, 0.01, 0.1\right)*\left({\tilde{S}_{14}}-{\tilde{S}_{13}}\right)\ge \ \tilde{Z} \\ &\left(0.01, 0.1, 0.3\right)*\left({\tilde{S}_{13}}-{\tilde{S}_{11}}\right)\ge \ \tilde{Z} \\ &\left(0.3, 0.5, 0.7\right)*\left({\tilde{S}_{11}}-{\tilde{S}_{12}}\right)\ge \ \tilde{Z} \\ &\left(0.5, 0.7, 0.9\right)*\left({\tilde{S}_{12}}-{\tilde{S}_{15}}\right)\ge \ \tilde{Z} \\ &\left(0.7, 0.9, 1\right)*\left({\tilde{S}_{15}}-{\tilde{S}_{16}}\right)\ge \ \tilde{Z} \\ &\left(0.9, 1, 1\right)*\left({\tilde{S}_{16}}\right)\ge \ \tilde{Z} \\ &\left(0.01, 0.01, 0.1\right)*\left({\tilde{S}_{23}}-{\tilde{S}_{24}}\right) \ge \ \tilde{Z} \\ &\left(0.01, 0.01, 0.1\right)*\left({\tilde{S}_{21}}-{\tilde{S}_{24}}\right)\ge \ \tilde{Z} \\ &\left(0.01, 0.1, 0.3\right)*\left({\tilde{S}_{24}}-{\tilde{S}_{22}}\right)\ge \ \tilde{Z} \\ &\left(0.3, 0.5, 0.7\right)*\left({\tilde{S}_{22}}-{\tilde{S}_{26}}\right)\ge \ \tilde{Z} \\ &\left(0.7, 0.9, 1\right)*\left({\tilde{S}_{26}}-{\tilde{S}_{25}}\right)\ge \ \tilde{Z} \\ &\left(0.9, 1, 1\right)*\left({\tilde{S}_{25}}\right)\ge \ \tilde{Z} \\ &\left(0.01, 0.01, 0.1\right)*\left({\tilde{S}_{31}}-{\tilde{S}_{33}}\right)\ge \ \tilde{Z} \\ &\left(0.01, 0.1, 3\right)*\left({\tilde{S}_{33}}-{\tilde{S}_{35}}\right)\ge \ \tilde{Z} \\ &\left(0.3, 0.5, 0.7\right)*\left({\tilde{S}_{35}}-{\tilde{S}_{34}}\right)\ge \ \tilde{Z} \\ &\left(0.5, 0.7, 0.9\right)*\left({\tilde{S}_{34}}-{\tilde{S}_{32}}\right)\ge \ \tilde{Z} \\ &\left(0.7, 0.9, 1\right)*\left({\tilde{S}_{32}}-{\tilde{S}_{36}}\right)\ge \ \tilde{Z} \\ &\left(0.9, 1, 1\right)*\left({\tilde{S}_{36}}\right)\ge \ \tilde{Z} \\ &{\tilde{S}_{11}}+{\tilde{S}_{12}}+{\tilde{S}_{13}}+{\tilde{S}_{14}}+{\tilde{S}_{15}}+{\tilde{S}_{16}}+{\tilde{S}_{21}}+{\tilde{S}_{22}}+{\tilde{S}_{23}}+{\tilde{S}_{24}}+{\tilde{S}_{25}}+{\tilde{S}_{26}}+{\tilde{S}_{31}}+{\tilde{S}_{32}}+{\tilde{S}_{33}}+{\tilde{S}_{34}}+{\tilde{S}_{35}} +{\tilde{S}_{36}}=(0.8, 1, 1.2) \\ &{\tilde{S}_{11}},{\tilde{S}_{12}},{\tilde{S}_{13}},{\tilde{S}_{14}},{\tilde{S}_{15}},{\tilde{S}_{16}}, {\tilde{S}_{21}},{\tilde{S}_{22}},{\tilde{S}_{23}},{\tilde{S}_{24}},{\tilde{S}_{25}},{\tilde{S}_{26}},{\tilde{S}_{31}},{\tilde{S}_{32}},{\tilde{S}_{33}},{\tilde{S}_{34}},{\tilde{S}_{35}},{\tilde{S}_{36}}\ge \ 0 \end{aligned}$$

(26)

After employing the Eq. (10) to solve the model (26), the results are shown in Table 9. Afterward, the Total Fuzzy Scores of each supplier can be calculated using the Eq. (22). The results are shown in Table 10. Further, what every decision-maker expects from a decision-making method is getting crispy or precise solutions. Thus, the next step could be the defuzzification of the Total Fuzzy Scores using the Eq. (23). The output, thus obtained, can be easily ranked, as shown in the last two columns of Table 10 and Fig. 5.

Table 10 Total fuzzy score of each supplier – Example 1

Fig. 5

The ranking of the alternatives – Example 1

One can see from Table 10 and Fig. 5 that the fourth supplier is the best one considering the importance of the predefined three attributes against which the suppliers were evaluated using the OPA-F. For the sake of convenience of the readers, one can express the prioritization as,

A4 > A1 > A3 > A2 > A5 > A6.

If one plots the triangular membership functions of each alternative, as available in Table 10, one can get a valuable illustration, as shown in Fig. 6. From the figure, one can see what makes an optimum supplier different from other competing suppliers. The most optimum supplier (A4) is represented through the dotted line.

Fig. 6

The plot of the membership functions of the alternatives – Example 1

4.2 Example 2: the case of incomplete data

Lack of knowledge in supply chain (SC) decision-making and incompleteness in supply/demand datasets is well-known in the literature. For instance, Wong and Johansen (2006) reported that decision-makers might lack knowledge of how the interrelationships between different variables may influence the physical flow behaviours over time. Javed et al. (2020c) reported incompleteness in the biofuel supply/demand datasets. Producing reliable results from insufficient, incomplete, or non-obtainable information is a challenge for almost all MADM techniques because of increasing uncertainty and complexity (Javed et al. 2020b). This challenge was widely experienced during the COVID-induced SC disruptions. Furthermore, not only the crisp numbers-driven MADM approaches, in many cases, even the fuzzy MADM methods have failed to handle MADM problems involving incomplete data. For example, Ren and Lützen (2017) noted that the fuzzy AHP method could not handle the problem containing incomplete information. In other words, fuzzy AHP cannot effectively achieve multi-criteria decision making when some information for decision-making is incomplete. This limitation can be outlined in other fuzzy MADM approaches as well. Therefore, to test the effectiveness of the OPA-F , it was necessary to test the model on a case involving incomplete data as well.

For this purpose, the case presented in Example 1 can be modified to bring it nearer to reality. Let us assume that our procurement manager was not sure about the material quality of the fourth supplier (A4), and he did not record his observation on it, resulting in a matrix of observations containing incomplete data, as shown in Table 11. Other conditions are consistent (i.e., Table 6 from Example 1 is applicable in Example 2 as well). The revised results, obtained through the execution of the algorithm of the OPA-F, have been presented in Tables 12, 13, 14.

Table 11 A Hypothetical Supplier Selection Problem – Example 2

Table 12 The fuzzy weights of the three attributes – Example 2

Table 13 Fuzzy Score of each supplier against each attribute – Example 2

Table 14 Total Fuzzy Score of each alternative – Example 2

One can see from Table 14 and Fig. 7 that the third supplier, which was earlier the second optimum alternative, has emerged as the most optimum alternative when the data is incomplete. The order of all suppliers is A3 > A1 > A2 > A5 > A4 > A6.

Fig. 7

The ranking of the alternatives – Example 2

Fig. 8

The plot of the membership functions of the alternatives – Example 2

A3 is the best supplier, and A6 is the worst supplier. If one plots the triangular membership functions of each alternative, as available in Table 14, one can get a handy illustration, as shown in Fig. 8. The input data of Example 2 was not only imprecise (linguistic information) but also incomplete. In Fig. 9, the comparative analysis of the two rankings, one obtained in Example 1 and the other obtained in Example 2, has been illustrated. The figure gives a very fitting picture of how the ranks switched their position when the data became incomplete.

Fig. 9

The comparative analysis of two rankings (Example 1 vs Example 2)

4.3 Example 3: a practical case study

Systems (individuals, organizations, supply chains, economies) not only affect the environment they are also influenced by the environment (Foster 2000: pp. 16; Ahmed et al. 2020). This reciprocal relationship help systems integrate with the environment, from which they consume the resources that are indispensable for their existence. Greening of the supply chains was one such attempt when supply chains ceded to environmental pressure. It also exposed the incompleteness of the theory of traditional SCM. The constructs surrounding the SCM theory are still unclear (Ansari and Kant 2017), leaving space for developments and testing new ideas, and fusing the existing ideas. Further, if one considers the complexities surrounding the supply chain network, one can argue that the conceptualization of green SCM is only partially complete (Wong et al. 2015). Gresilient SCM is one such attempt to overcome the deficiency. Gresilience can be defined as the ability of an environmentally sustainable system to recover quickly and effectively from a disruption. If this system is a supply chain, then the associated Gresilience can be called the supply chain gresilience. In the current study, supply chain resilience is a three-dimensional construct involving (a) Speed of Recovery (or Recovery Time) [C1; +], (b) Recovery Level [C2; +], and (c) Loss of Performance while Recovering [C3; -]. This construct is inspired by the work of Behzadi et al. (2020). In the current study, green supply chain is a four-dimensional construct involving (a) Efficient Energy Consumption [C4; +], (b) Efficient Material Use [C5; +], (c) Non-Product (Waste) Output [C6; -], and (d) Pollutant Releases [C7; -]. + and - represent higher-the-better and lower-the-better attributes, respectively. This construct is inspired by Ditz and Ranganathan's classification of the industrial environmental performance metrics, as reported in NAS (1999: pp. 30). The framework of Gresilient supply chain management is shown in Fig. 10. For the study, the data was collected from three respondents working in the procurement department of a kitchen utensils manufacturing company in Jiangsu, P. R. China. This company had experienced lockdown during China's successful fight against the COVID-19 pandemic, and the respondents were the eyewitness to the suppliers' performance loss during the lockdown and recovery when the lockdown was lifted. Each one was associated with the company for more than three years. The collected data is shown in Table 15. The lower-the-better attributes are reversed; thus, all variables have the same direction. In Table 15, A1, A2, A3 and A4 are four local suppliers of their company, and C1, C2…, and C7 are the seven attributes.

Fig. 10

The framework of Gresilient supply chain management

Table 15 Observations of three DMs concerning four Gresilient suppliers

The results obtained through the execution of the OPA-F on the data are shown in Tables 16, 17, and 18. Figure 11 shows the decision-makers' observations about the weight of supply chain resilience were relatively more consistent than their observations about the green aspect of the supply chain. This fact can easily be understood if one considers their company's recent experience with the disruptions that came along with the COVID-19 pandemic and unprecedently tested the resilience of their company and its suppliers.

Table 16 The fuzzy weights of the seven attributes – Gresilient Supplier Selection

Table 17 Fuzzy Score of each supplier with respect to each attribute – Gresilient Supplier Selection

Table 18 Total fuzzy score of each alternative – Gresilient Supplier Selection

Fig. 11

Optimal fuzzy weights of the five attributes – Gresilient Supplier Selection

The final ranking of their suppliers based on their Gresilience can be observed in Fig. 12. It is apparent that the third supplier, A3, outperformed others. If all suppliers took a lesson from the recent disruptions, they are more likely to perform better if the second wave of the disruptions, or new disruption, emerges. The plot of the membership functions of the suppliers is shown in Fig. 13

Fig. 12

The ranking of suppliers based on their Gresilience – Gresilient Supplier Selection

Fig. 13

The plot of the membership functions of the alternatives – Gresilient Supplier Selection

5 Comparative analysis

In this section, the results of OPA-F and that of the Fuzzy TOPSIS are mutually compared. Table 19 shows the obtained ranks through OPA-F and Fuzzy TOPSIS based on the problem discussed by Chen (2000), the pioneer of the Fuzzy TOPSIS. As can be seen from Table 19, the rankings from both methods are comparable. Based on the results, A2 is the best alternative for this problem. Among MADM approaches, there is not any specific approach that can prove that the results of a specific method are definitely correct or not. However, solving a problem using different methods is a common practice to show the validity of the results. Therefore, in the current study, we have compared the obtained results with the Fuzzy TOPSIS method since the input data of OPA-F and the Fuzzy TOPSIS is comparable.

Table 19 The results of OPA-F and TOPSIS-F method

It is worth noting that the weights of attributes can be calculated using the OPA-F while Fuzzy TOPSIS cannot calculate the weights of attributes. In the current case, the ranks are comparable with the ranks obtained by the Fuzzy TOPSIS. Therefore, the proposed method is rational and feasible. Here, it should be noted that even though both methods achieved comparable results, the OPA-F is likely more useful than other fuzzy MADM approaches for some reasons; (a) Most fuzzy MADM approaches, e.g., the Fuzzy AHP, require pairwise comparisons and thus consistency ratio, directly influences the reliability of the ranks, (b) Many fuzzy MADM approaches, e.g., Fuzzy TOPSIS, give ranks but do not provide weights of the alternatives, (c) Most fuzzy MADM methods require complete data sets, and cannot handle the problems where complete data is unavailable or cannot be obtained, etc. On the other hand, the OPA-F neither requires pairwise comparisons nor any consistency measure. It can also handle incomplete data and provide weights for the criteria as well without requiring the experts to allocate weights to the criteria.

6 Conclusion and recommendations

In the wake of the supply chain disruptions that followed the COVID-19 pandemic, complexities and uncertainties surrounding decision-making processes have become more apparent. Decision-making is the primary task of supply chain managers, and the success (and failure) of their work units depends on the optimality (and sub-optimality) of their decisions. The literature is full of MADM methods to guide decision-makers in their quest for optimal solutions to the problems. Each method has its strengths and limitations. Thus, some scholars came up with hybrid methods where strengths of different methods are aggregated; however, in the process, the limitations are also inherited. For example, the fuzzy set theory was integrated into the AHP to handle linguistic information. However, the resulting method was only partially effective because of the Fuzzy AHP's inability to handle incomplete data, which is common in real-world group decision-making problems. Further, the AHP's dependence on pairwise comparisons and consistency ratio was inherited by the Fuzzy AHP as well. Similarly, when the Fuzzy TOPSIS was introduced even though it enabled the new methodology to handle linguistic variables, the inherent limitation of TOPSIS that prevent it from producing the weights of the attributes was evident in the Fuzzy TOPSIS as well. The development of the Ordinal Priority Approach (OPA) has overwhelmed several intrinsic limitations of the existing MADM methods, e.g., dependence on pairwise comparisons, decision matrices, consistency ratio, normalization, aggregation operators, etc. The OPA represents an innovative decision-making technology that is both novel and powerful because of its foundation on a powerful mathematical programming approach rather than on decision matrices. However, its dependence on ordinal information prevented it from handling linguistic information, thus making it unable to handle problems characterized by impression or fuzziness. In the current study, an extension to the OPA has been proposed as the OPA for Fuzzy Linguistic Information (OPA-F), which has extended its applicability for the problems containing linguistic information as well. The new method inherits all key strengths of the original OPA while relieving it from its fundamental limitation. The three examples, involving both complete and incomplete data, presented in the current study, offered detailed execution of the OPA-F and its validity. The results are convincing and, when compared with that of Fuzzy TOPSIS, turned out to be more useful. Furthermore, through the introduction of a novel approach of fuzzy linear programming in the MADM context, the current study opens a door for subsequent development of the theory of fuzzy MADM. The COVID-19 pandemic has highlighted the significance of new technologies to counter emerging challenges however how the OPA-F is going to meet the needs of decision-makers in the post-COVID era will be seen in future, as it sees application on diverse range of practical problems.

Even though capital accumulation, the core dynamic defining the existence of any business, can be threatened by environmental constraints on supplies of its needed material use-values, it should not prevent humankind from looking for new ways to put sustainable development in command of production (Burkett 2006: pp. 294). Thus, it is hoped that the discussions on gresilient supply chains may facilitate the journey towards ecologically sensitive supply chains in the future. By viewing the supply chain and its environment as a dialectical whole and by recognizing the importance of the supply chain's resilience aspect, in particular, and green aspect, in general, the study argues gresilient supply chain management is an appropriate approach to evaluate the performance of suppliers, which are hit by the COVID-19 like disruptions. To avoid such disruptions in the future, the study argues the extension of traditional supply chain management to gresilient supply chain management and proposes a new construct for evaluating suppliers based on gresilience. Further, the study introduces the definition of 'gresilience.' Since gresilience is a new concept in supply chain management, there are a lot of theoretical and practical works need to be done that involves revisiting its utility, definition and construct.