Abstract
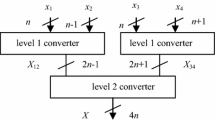
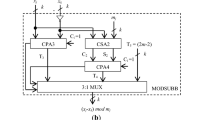
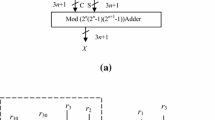
In this paper, we describe a two-stage reverse converter for the four moduli superset {2k, 2n−1, 2n+1, 2n+1+1} for n ≤ k ≤ 2n. In the first stage, a three moduli converter based on Chinese remainder theorem (CRT) is used for the subset {2k, 2n−1, 2n+1} to obtain the decoded number. A second stage obtains the final binary number considering this number and the residue corresponding to the fourth modulus (2n+1+1) using MRC to obtain the final decoded number. Complete architectures is described together with ASIC implementation results as well as comparison with reverse converters described earlier in literature with k = n.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Omondi A and Premkumar A B 2007 Residue Number System Theory and Implementation. Imperial College Press, London
Ananda Mohan P V 2002 Residue Number Systems: Algorithms and VLSI Architectures. Kluwer Academic Publishers, New York
Chaves R and Sousa L 2004{2n+1, 2n+k, 2n−1}: A new RNS moduli set extension. In: Proc. EuromicroSymp. Digital System Design, Rennes, France, 31 August: 210–217
Vinod A P and Premkumar A B 2000 A memoryless reverse converter for the 4-moduli superset {2n−1, 2n, 2n+1, 2n+1–1}. J. Circuit Syst. Comput. 10: 85–99
Bhardwaj M, Srikanthan T and Clarke C T 1999 A reverse converter for the 4 moduli super set {2n−1, 2n, 2n+1, 2n+1+1}. In: Proceedings of the IEEE Conference on Computer Arithmetic. 14 April: 168–175
Ananda Mohan P V and Premkumar A B 2007 RNS to Binaryconverters for two four moduli sets 2n–1, 2n, 2n+1, 2n+1−1 and {2n−1, 2n, 2n+1, 2n+1+1}. IEEE Trans. Circuits Syst. I. 54: 1245–1254
Cao B, Srikanthan T and Chang C H 2005 Efficient reverse converters for the four-moduli sets 2n–1, 2n, 2n+1, 2n+1– 1 and {2n−1, 2n, 2n+1, 2n–1–1}. IEEE Proc. Comput. Digit. Tech. 152: 687–696
Sousa L, Antao S and Chaves R 2013 On the design of RNS reverse converters for the four-moduli set {2n+1, 2n– 1, 2n, 2n+1+1}. IEEE Trans. VLSI Syst. 21: 1945–1949
Skavantzos A, Abdallah M, Stouraitis T and Schinianakis D 2009 Design of a balanced 8-modulus RNS. Proceedings of IEEE ISCAS. 13 December: 61–64
Madhavilatha M V N, Racch Rashmi Ramesh and Ananda Mohan P V 2020 An improved RNS-to-Binary converter for 7-modulus set 2n−5−1, 2n−3−1, 2n–2 +1, 2n−1−1, 2n–1+1, 2n, 2n +1 for n even. Sadhana Acad. Proc. Eng. Sci. 45: 239
Chalivendra G, Hanumaiah Vand Vrudhula S 2011 A new balanced 4-moduli set {2k, 2n−1, 2n+1, 2n+1−1} and its reverse converter design for efficient reverse converter implementation. Proc. ACM GSVLSI, Lausanne, Switzerland. 2 May: 139–144
Patronik P and Piestrak S 2013 Design of Reverse Converters for General RNS Moduli Sets {2k, 2n–1, 2n+1, 2n+1− 1} and {2k, 2n–1, 2n+1, 2n−1 −1} (n even). IEEE Trans. Circuits Syst. I: RegularPapers. 12: 1687–1700
Tyagi A 1993 A reduced-area scheme for carry-select adders. IEEE Trans. Comput. 42: 1163–1170
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Latha, M.V.N.M., Rachh, R.R. & Mohan, P.V.A. Residue to binary converter for the extended four moduli set {2k, 2n−1, 2n+1, 2n+1+1} for n odd. Sādhanā 48, 66 (2023). https://doi.org/10.1007/s12046-023-02118-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12046-023-02118-y