Skip to main content
SpringerLink
Log in

Optimal time policy for deteriorating items of two-warehouse inventory system with time and stock dependent demand and partial backlogging

  • Published:
Sādhanā Aims and scope Submit manuscript

Abstract

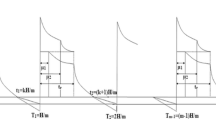
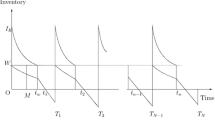
We consider the problem of a two-warehouse inventory system under the effect of stock dependent demand. There are two warehouses to store the goods in which the first is rented warehouse and the second is own warehouse that deteriorates with two different rates. The aim of this study is to determine the optimal order quantity to maximize the profit of the projected model. Finally, some numerical examples and sensitivity analysis of parameters are made to validate the results of the proposed model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4

Similar content being viewed by others

References

  1. Skouri K, Konstantaras I, Papachristors S and Ganas I 2009 Inventory models with ramp type demand rate, partial backlogging and Weibull distribution rate. Euro. J. Oper. Res. 192: 79–92

    Article  MATH  Google Scholar 

  2. Wee H M, Yu J C P and Law S T 2005 Two-warehouses with inventory models for partial backlogging and Weibull distribution deteriorating items under inflation. J. Chinese Inst. Ind. Eng. 22: 451–462

    Google Scholar 

  3. Yang H L 2006 Two-warehouse partial backlogging inventory model for deteriorating items under inflation. Int. J. Prod. Econ. 103: 362–370

    Article  Google Scholar 

  4. Lo S T, Wee H M and Huang W C 2007 An integrated production-inventory model with imperfect production processes and Weibull distribution deterioration under inflation. Int. J. Prod. Econ. 106: 248–260

    Article  Google Scholar 

  5. Skouri K and Konstantaras I 2009 Order level inventory models for deteriorating seasonable/fashionable products with time dependent demand and shortage. Math. Problem Eng. 2009: 1–24

    Article  MathSciNet  MATH  Google Scholar 

  6. Yang H L 2012 Two-warehouse partial backlogging inventory models with three-parameter Weibull distribution deterioration under inflation. Int. J. Product. Econ. 138: 107–116

    Article  Google Scholar 

  7. Chakrabarty T, Giri B C and Chaudhuri K S 1998 An EQO model for items with Weibull distribution deterioration, shortages and trend demand: An extension of Philip’s model. Comput. Oper. Res. 25: 649–657

    Article  MATH  Google Scholar 

  8. Dave U and Patel L K 2006 Policy inventory model for deteriorating items with time proportional demand. J. Oper. Res. Soc. 32: 137–142

    Article  MATH  Google Scholar 

  9. Ghare P M and Shrader G F 1963 A model for exponentially decaying inventory. J. Ind. Eng.14: 238–243

    Google Scholar 

  10. Giri B C, Jalan A K and Chaudhuri K S 2003 Economics order quantity model with Weibull deterioration distribution, shortages and ramp-type demand. Int. J. Syst. Sci. 34: 237–243

    Article  MathSciNet  MATH  Google Scholar 

  11. Hariga M A 1996 Optimal EOQ models for deteriorating items with time-varying demand. J. Oper. Res. Soc. 47: 1228–1246

    Article  MATH  Google Scholar 

  12. Misra R B 1975 Optimal production lot-size model for a system with deterioration inventory. Int. J. Prod. Res. 13: 495–505

    Article  Google Scholar 

  13. Philip G C 1974 A generalized EOQ model for items with Weibull distribution deterioration. AIIE Trans. 6: 159–162

    Article  Google Scholar 

  14. Teng J T Chern, M S Yang H L and Wang Y J 1999 Deterministic lot-size inventory model with shortage and deterioration for fluctuation demand. Oper. Res. Lett. 24: 65–72

    Article  MathSciNet  MATH  Google Scholar 

  15. Covert R P and Philip G C 1973 An EOQ model for items with Weibull distribution deterioration. AIIE Trans. 5: 323–326

    Article  Google Scholar 

  16. Goyal S K and Giri B C 2001 Recent trends in modeling of deteriorating inventory. Eur. J. Oper. Res. 134: 1–6

    Article  MathSciNet  MATH  Google Scholar 

  17. Jaggi C K and Tiwari S 2014 Two-warehouse inventory model for non-instantaneous deteriorating items with price dependent demand and time-varying holding cost. Math. Model. Appl. 225–238

  18. Daultani Y, Kumar S, Vaidya O S and Tiwari M K 2015 A supply chain network equilibrium model for operational and opportunism risk mitigation. Int. J. Prod. Res. 53: 5685–5715

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Indian School of Mines, Dhanbad, 826004, India

    Shiv Kumar & Abhay Kumar Singh

Authors
  1. Shiv Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abhay Kumar Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shiv Kumar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumar, S., Singh, A.K. Optimal time policy for deteriorating items of two-warehouse inventory system with time and stock dependent demand and partial backlogging. Sādhanā 41, 541–548 (2016). https://doi.org/10.1007/s12046-016-0490-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12046-016-0490-y

Keywords

Search

Navigation