Skip to main content
SpringerLink
Log in

Buckling analysis and small scale effect of biaxially compressed graphene sheets using non-local elasticity theory

  • Published:
Sadhana Aims and scope Submit manuscript

Abstract

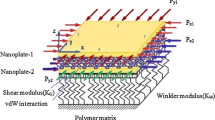
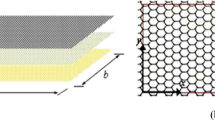
In this paper, buckling analysis of biaxially compressed graphene sheets with non-local elasticity theory is reported. The equations of motion for graphene sheet are derived using non-local local elasticity theory. Levy’s approach has been used to solve the governing equations for various boundary conditions of the graphene sheet. Present results from Levy’s solution agree with the results for all edges simply supported available in the literature. Further, the effect of the (i) non-local parameter, (ii) size of the graphene sheet and (iii) various boundary conditions on the critical buckling loads of the graphene sheets are investigated. It is observed that non-local parameter and boundary conditions significantly influence the critical buckling loads of the small size graphene sheets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Fig. 8
Figure 9
Figure 10
Figure 11
Figure 12
Figure 13
Figure 14

Similar content being viewed by others

References

  • Ball P 2001 Roll up for the revolution. Nature 414: 142–144

    Article  Google Scholar 

  • Baughman R H, Zakhidov A A and de Heer W A 2002 Carbon nanotubes–the route toward applications. Science 297(5582): 787–792

    Article  Google Scholar 

  • Behfar K and Naghdabadi R 2005 Nanoscale vibrational analysis of a multi-layered graphene sheet embedded in an elastic medium. Compos. Sci. Tech. 65(7–8): 1159–1164

    Article  Google Scholar 

  • Duan W H and Wang C M 2007 Exact solutions for axisymmetric bending of micro/nanoscale circular plates based on non-local plate theory. Nanotechnology 18(38): 385704

    Article  Google Scholar 

  • Eringen A C 1983 On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 54: 4703

    Article  Google Scholar 

  • Eringen A C 2002 Nonlocal continuum field theories. New York: Springer Verlag

    MATH  Google Scholar 

  • Ghorbanpour Arani A, Rahmani R and Arefmanesh A 2008 Elastic buckling analysis of single-walled carbon nanotube under combined loading by using the ANSYS software. Physica E 40(7): 2390–2395

    Article  Google Scholar 

  • Ghorbanpour Arani A, Mohammadimehr M, Arefmanesh A and Ghasemi A 2010 Transverse vibration of short carbon nanotubes using cylindrical shell and beam models. J. Mech. Eng. Sci. 224(3): 745–756

    Article  Google Scholar 

  • Ghorbanpour Arani A, Mohammadimehr M, Saidi A R, Shogaei S and Arefmanesh A 2011 Thermal buckling analysis of double walled carbon nano tubes considering the small scale effect. J. Mech. Eng. Sci. 225(1), 248–256

    Google Scholar 

  • Gibson R F, Ayorinde E O and Wen Y-F 2007 Vibrations of carbon nanotubes and their composites: A review. Compos. Sci. Technol. 67(1): 1–28

    Article  Google Scholar 

  • Hsu M 2010 Dynamic analysis of multi-walled carbon nanotubes using the differential quadrature method. J. Mech. Eng. Sci. 224(3): 731–744

    Article  Google Scholar 

  • Iijima S 1991 Helical microtubules of graphitic carbon. Nature 354: 56–58

    Article  Google Scholar 

  • Karaoglu P and Aydogdu M 2010 On the forced vibration of carbon nanotubes via a non-local Euler–Bernoulli beam model. J. Mech. Eng. Sci. 224(2): 497–503

    Article  Google Scholar 

  • Kong X Y, Ding Y, Yang R and Wang Z L 2004 Single-crystal nanorings formed by epitaxial self-coiling of polar nanobelts. Science 303(5662): 1348–1351

    Article  Google Scholar 

  • Kroto H W 1985 C60: Buckminsterfullerene. Nature 318: 162–163

    Article  Google Scholar 

  • Kitipornchai S, He X Q and Liew K M 2005 Continuum model for the vibration of multilayered graphene sheets. Phys. Rev. B 72: 075443

    Article  Google Scholar 

  • Liew K M, He X Q and Kitipornchai S 2006 Predicting nanovibration of multi-layered graphene sheets embedded in an elastic matrix. Acta Mater. 54(16): 4229–4236

    Article  Google Scholar 

  • Lu P, Lee H P, Lu C and Zhang P Q 2007 Application of nonlocal beam models for carbon nanotubes. Int. J. Solids Struct. 44(16): 5289–5300

    Article  MATH  Google Scholar 

  • Murmu T and Pradhan S C 2008 Buckling analysis of beam on Winkler foundation by using MDQM and nonlocal theory. J. Aero. Sci. Technol. 60(3): 206–215

    Google Scholar 

  • Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V and Firsov A A 2004 Electric field effect in atomically thin carbon films. Science 306(5696): 666–669

    Article  Google Scholar 

  • Peddieson J, Buchanan G R and McNitt R P 2003 Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 41(3–5): 305–312

    Article  Google Scholar 

  • Phadikar J K and Pradhan S C 2008 Nonlinear finite element model of single wall carbon nano tubes. J. Inst. Eng. (India) Metallurgy Mater. Eng. Div. 89: 3–8

    Google Scholar 

  • Phadikar J K and Pradhan S C 2009 Bending, vibration and buckling analysis of non homogenous nanotubes using nonlocal elasticity theory and GDQ method. Struct. Eng. Mech. 33(2): 193–213

    Google Scholar 

  • Pradhan S C 2009 Buckling of single layer graphene sheet based on nonlocal elasticity and higher order shear deformation theory. Phys. Lett. A 373: 4182–4188

    Article  MATH  Google Scholar 

  • Pradhan S C 2012 Nonlocal finite element analysis and small scale effects of CNTs with Timoshenko beam theory. Finite Elements in Analysis and Design 50: 8–20

    Article  Google Scholar 

  • Pradhan S C and Murmu T 2009a Small scale effect on the buckling of single-layered graphene sheets under bi-axial compression via nonlocal continuum mechanics. Comput. Mat. Sci. 47: 268–274

    Article  Google Scholar 

  • Pradhan S C and Murmu T 2009b Differential quadrature method for vibration analysis of beam on Winkler foundation based on nonlocal elastic theory. J. Inst. Eng. (India) Metallurgy Mater. Eng. Div. 89: 3–12

    Google Scholar 

  • Pradhan S C and Murmu T 2009c Small-scale effect on the free in-plane vibration of nanoplates by nonlocal continuum model. Physica E 41(8): 1628–1633

    Article  Google Scholar 

  • Pradhan S C and Murmu T 2009d Thermo-mechanical vibration of FGM sandwich beam under variable elastic foundation using differential quadrature method. J. Sound Vib. 321: 342–362

    Article  Google Scholar 

  • Pradhan S C and Murmu T 2010a Application of nonlocal elasticity and DQM in the flapwise bending vibration of a rotating nanocantilever. Physica E 42: 1944–1949

    Article  Google Scholar 

  • Pradhan S C and Murmu T 2010b Small scale effect on the buckling analysis of single-layered graphene sheet embedded in an elastic medium based on nonlocal plate theory. Physica E 42(5): 1293–1301

    Article  Google Scholar 

  • Pradhan S C and Phadikar J K 2009a Bending, buckling and vibration analyses of nonhomogeneous nanotubes using GDQ and nonlocal elasticity theory. Struct. Eng. Mech. Int. J. 33(2): 193–213

    Google Scholar 

  • Pradhan S C and Phadikar J K 2009b Small scale effect on vibration of embedded multilayered graphene sheets based on nonlocal continuum models. Phys. Lett. A 373(11): 1062–1069

    Article  MATH  Google Scholar 

  • Pradhan S C and Phadikar J K 2010 Scale effect and buckling analysis of multilayered graphene sheets based on nonlocal continuum mechanics. J. Comput. Theor. Nanosci. 7: 1–7

    Article  Google Scholar 

  • Pradhan S C and Sahu B 2010 Vibration of single layer graphene sheet based on nonlocal elasticity and higher order shear deformation theory. J. Comput. Theor. Nanosci. 7(6): 1042–1050

    Article  Google Scholar 

  • Pradhan S C and Sarkar A 2009 Analyses of tapered FGM beams with nonlocal theory. Struct. Eng. Mech. Int. J. 32(6): 811–833

    Google Scholar 

  • Reddy J N 1997 Mechanics of laminated composite plates: Theory and analysis. Boca Raton, FL: Chemical Rubber Company

    MATH  Google Scholar 

  • Reddy J N 2007 Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 45(2–8): 288–307

    Article  MATH  Google Scholar 

  • Stankovich S, Dikin D A, Dommett G H B, Kohlhaas K M, Zimney E J, Stach E A, Piner R D, Nguyen S T and Ruoff R S, 2006 Graphene based composite materials. Nature 442: 282–286

    Article  Google Scholar 

  • Thostenson E T, Ren Z and Chou T-W 2001 Advances in the science and technology of carbon nanotubes and their composites: a review. Compos. Sci. Tech. 61(13): 1899–1912

    Article  Google Scholar 

  • Timoshenko S P and Gere J M 1985 Theory of elastic stability, Singapore: McGraw Hill International Book Company

    Google Scholar 

  • Wang L, Ni Q, Li M and Qian Q 2008 The thermal effect on vibration and instability of carbon nanotubes conveying fluid. Physica E 40(10): 3179–3182

    Article  Google Scholar 

  • Wang Q and Vardan V K 2006 Wave characteristics of carbon nanotubes. Int. J. Solids Struct. 43(2): 254–265

    Article  MATH  Google Scholar 

Download references

Acknowledgements

Author thanks Mr. M Pant, undergraduate student of Indian Institute of Technology Kharagpur for some computational results.

Author information

Authors and Affiliations

  1. Department of Aerospace Engineering, Indian Institute of Technology, Kharagpur, 721 302, India

    S C PRADHAN

Authors
  1. S C PRADHAN
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S C PRADHAN.

Rights and permissions

Reprints and permissions

About this article

Cite this article

PRADHAN, S.C. Buckling analysis and small scale effect of biaxially compressed graphene sheets using non-local elasticity theory. Sadhana 37, 461–480 (2012). https://doi.org/10.1007/s12046-012-0088-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12046-012-0088-y

Keywords

Search

Navigation