Abstract
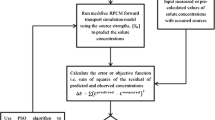
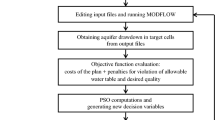
Remediation of the groundwater contamination problem is a tedious, time consuming and expensive process. Pump and treat (PAT) is one of the commonly used techniques for groundwater remediation in which the contaminated groundwater is pumped, treated and put back to the aquifer system or other sources. Developing simulation-optimization (S/O) model proved to be very useful in the design process of an effective PAT system. Simulation models help in predicting the spatial and temporal variation of the contamination plume while optimization models help in minimizing the cost of pumping. Generally, grid or mesh based models such as Finite Difference Method (FDM) or Finite Element Methods (FEM) is used for the groundwater flow and transport simulation. But it is found that grid/mesh generation is a time consuming process. Therefore, recently Meshfree (MFree) based numerical models are developed to avoid this difficulty of meshing and remeshing. MFree Point Collocation Method (PCM) is a simple meshfree method used for the simulation of coupled groundwater flow and contaminant transport. For groundwater optimization problems, even though number of methods such as linear programming, nonlinear programming, etc. are available, evolutionary algorithm based techniques such as genetic algorithm (GA) and particle swarm optimization (PSO) are found to be very effective.
In this paper, a simulation model using MFree PCM for confined groundwater flow and transport and a PSO based single objective optimization model are developed and coupled to get an effective S/O model for groundwater remediation using PAT. The S/O model based on PCM and PSO is applied for a polluted hypothetical confined aquifer and its performance is compared with Finite Element Method–Binary Coded Genetic Algorithm (FEM–GA) model. It is found that both the models are in good agreement with each other showing the applicability of the present approach. The PCM–PSO based S/O model is simple and more effective in groundwater contamination remediation design using PAT.
Similar content being viewed by others
References
Ahlfeld D P, Mulvey M J, Pinder G F and Wood E F 1988 Contaminated groundwater remediation design using simulation, optimization, and sensitivity theory Model development. Water Resour. Res. 24(3): 431–441
Bear J 1979 Hydraulics of groundwater, New York: McGraw Hill Publishing
Chang L C, Shoemaker C A and Liu P L-F 1992 Optimal time varying pumping rates for groundwater remediation: application of a constrained optimal algorithm. Water Resour. Res. 28(12): 3157–3173
Deb K 1995 Optimization for engineering design, New Delhi: Prentice Hall of India
Eberhart R C, Simpson P and Dobbins R 1996 Computational Intelligence PC Tools, Academic Press
Eugene Agyei, Douglas Munch P G and Patrick Burger P E 2005 Application of optimization modeling to water resource planning in East-Central Florida, St. Johns River Water Management District, Technical Publication SJ2005–2, Palatka, Florida
Freeze R A and Cherry J A 1979 Groundwater, Englewood Cliffs, NJ: Prentice Hall-INC
Gill P E, Murray W, Saunders A, and Wright M H (1984) Aquifer reclamation design: The use of contaminant transport simulation combined with nonlinear programming. Water Resour. Res. 20(4): 415–427
Guan J and Aral M M 1999 Optimal remediation with well locations and pumping rates selected as continuous decision variables. J. Hydrol. 221: 20–42
Huang C and Mayer A S 1997 Pump-and-treat optimization using well locations and pumping rates as decision variables. Water Resour. Res. 33(5): 207–222
Kansa E J 1990 Multiquadrics-A scattered data approximation scheme with application to computational fluid dynamics II (Solutions to parabolic, hyperbolic and elliptic Partial Differential Equation). J. Computers Mathematical Applications 19(8/9): 147–161
Kennedy J and Eberhart R C 1995 Particle swarm optimization. Proc. IEEE Int’l. Conf. on Neural Networks, IV, 1942–1948. Piscataway, NJ: IEEE Service Center
Kennedy James and Eberhart R C 2001 Swarm intelligence, CA, USA: Academic press
Liggett J A and Liu P L-F 1983 The boundary integral equation method for porous media flow, London: George Allen and Unwin
Liu G R and Gu Y T 2005 An introduction to meshfree methods and their programming, Dordrecht, Berlin, Heidelberg, New York: Springer
Marino M A 1974 Longitudinal dispersion in saturated porous media. J. Hydraulics Division, ASCE, 100 (HY1), 151–157
Mategaonkar M and Eldho T I 2011 Simulation of groundwater flow in unconfined aquifer using meshfree polynomial point collocation method. Eng. Analysis with Boundary Elements 35: 700–707
Mategaonkar M and Eldho T I 2012 Two-dimensional contaminant transport modeling using meshfree point collocation method (PCM). Eng. Analysis with Boundary Elements 36: 551–561
Mondal Arpita 2007 FEM-GA based simulation–optimization models for groundwater remediation, M.Tech. Thesis, IIT, Bombay
Mondal Arpita, Eldho T I and Gurunadhrao V V S 2010 Multiobjective groundwater remediation system design using coupled finite element model and nondominated sorting genetic algorithm II. J. Hydrologic Eng. (ASCE) 15(5): 350–359
Parsopoulas K E and Vrahatis M N 2002 Recent approaches to global optimization problems through particle swarm optimization. Natural computing (1): 235–306, The Netherlands: Kluwer Academic Publishers
Parsopoulos K E, Plagianakos V P, Magoulas G D and Vrahatis M N 2001 Stretching technique for obtaining global minimizers through particle swarm optimization. Proceedings of the Workshop on Particle Swarm Optimization, Indianapolis, IN: Purdue School of Engineering and Technology, IUPUI (in press)
Prasad K L and Rastogi A K 2001 Estimating net aquifer recharge and zonal hydraulic conductivity values for Mahi right bank canal project Area, India by genetic algorithm. J. Hydrol. 243(3–4): 149–161
Shawn M L, Rabideau A J and Craig J R 2006 Pump-and-treat optimization using analytic element method flow models Advances in water resources. J. Advances Water Resour. 29(5): 760–775
Wang H and Anderson M P 1982 Introduction to groundwater modeling finite difference and finite element methods, New York: W H Freeman and Company. http://www.hc-sc.gc.ca/ewh-semt/pubs/water-eau/doc_sup-appui/tds-mdt/index_e.html
Wang M and Zheng C 1997 Optimal remediation policy selection under general conditions. Groundwater 35(5): 757–764
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
MEENAL, M., ELDHO, T.I. Simulation–optimization model for groundwater contamination remediation using meshfree point collocation method and particle swarm optimization. Sadhana 37, 351–369 (2012). https://doi.org/10.1007/s12046-012-0086-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12046-012-0086-0