Skip to main content
SpringerLink
Log in

Chaos from jerk circuit

  • Classroom
  • Published:
Resonance Aims and scope Submit manuscript

Abstract

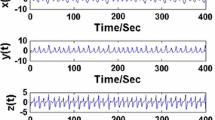
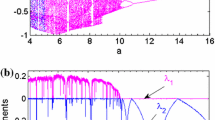
We present an experimental circuit realization of a simple jerk equation with modulus nonlinearity and study the chaotic behaviour as a function of a variable control parameter. The third order differential equation has been realized using commonly available opamps and the nonlinearity using a pair of diodes. The experiments indicate that chaotic behaviour indeed emerges through the period doubling route as the parameter is changed. This work is instructive to show students the phase plots as a function of the control parameter and determine the Feigenbaum constant.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Suggested Reading

  1. E N Lorenz, Deterministic nonperiodic flow, J. Atmos. Sci., Vol.20, pp.130–141, 1963.

    Article  Google Scholar 

  2. O E Rössler, An equation for continuous chaos, Phys. Lett. A, Vol.57, pp.397–398, 1976.

    Article  Google Scholar 

  3. OE Rössler, Continuous chaos-four prototype equations, Ann. (N.Y.) Acad. Sci., Vol.316, pp.376–392, 1979.

    Article  Google Scholar 

  4. F M A Salam and S S Sastry, Dynamics of the forced Josephson junction circuit: the regions of chaos, IEEE Trans. Circuits Syst., Vol.32, pp.784–796, 1985.

    Article  Google Scholar 

  5. T Endo and L O Chua, Chaos from phase locked loops, IEEE Trans. Circuits Syst., Vol.35, pp.987–1003, 1988.

    Article  Google Scholar 

  6. K Watada, T Endo and H Seishi, Shilnikov orbits in an autonomous third order chaotic phase locked loop, IEEE Trans. Circuits Syst., Vol.45, pp.979–983, 1998.

    Article  Google Scholar 

  7. JC Sprott, Anew class of chaotic circuit, Phys. Lett.A, Vol.266,pp.19–23, 2000.

    Article  Google Scholar 

  8. J C Sprott, Simple chaotic systems and circuits, Am. J. Phys., Vol.68, pp.758–763, 2000.

    Article  Google Scholar 

  9. G Prakash and K Mitra, Chaos in a simple electronic circuit, National Conf. on NSD, pp.325–328, 2003.

  10. MW Hirsch and S Smale, Differential Equations, Dynamical Systems and Linear Algebra, Academic Press, New York, 1974.

    Google Scholar 

  11. J C Sprott and S J Linz, Algebraically simple chaotic flows, Int. J. Chaos Theory and Appls., Vol.5, pp.3–20, 2000.

    Google Scholar 

  12. http://www.national.com/mpf/TL/TL082.html

Download references

Author information

Authors and Affiliations

  1. Department of Physics, National Institute of Technology, Durgapur, 713209, India

    K. B. Shaik & M. K. Mandal

Authors
  1. K. B. Shaik
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. K. Mandal
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shaik, K.B., Mandal, M.K. Chaos from jerk circuit. Reson 15, 257–267 (2010). https://doi.org/10.1007/s12045-010-0039-z

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12045-010-0039-z

Keywords

Search

Navigation