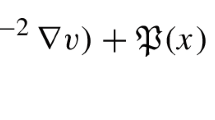Abstract
In this work, we study the Nehari manifold and its application to the following sub-elliptic system involving the multiple critical Sobolev exponents:
where \(\Omega \) is an open bounded subset of \(\mathbb {G}\) with smooth boundary, \(-\Delta _{\mathbb {G}}\) is the sub-Laplacian on Carnot group \(\mathbb {G}\), \(\lambda > 0\) is a parameter, \(1< q < 2\), \(\alpha \), \(\beta >1\), \(\alpha +\beta =2^*\), \(2^*=\frac{2Q}{Q-2}\) is the critical Sobolev exponent, and Q is the homogeneous dimension of \(\mathbb {G}\). By exploiting the Nehari manifold and variational methods, we prove that the system has at least two positive solutions when the pair of the parameters \((\mu ,\nu )\) belongs to a certain subset of \(\mathbb {R}^{2}_{+}\).
Similar content being viewed by others
References
Ambrosetti A, Brezis H and Cerami G, Combined effects of concave and convex nonlinearities in some elliptic problems, J. Funct. Anal. 122 (2) (1994) 519–543
Bartsch T and Willem M, On an elliptic equation with concave and convex nonlinearities, Proc. Amer. Math. Soc. 123 (1995) 3555–3561
Bonfiglioli A and Uguzzoni F, Nonlinear Liouville theorems for some critical problems on H-type groups, J. Functional Analysis 207 (2004) 161–215
Bonfiglioli A, Lanconelli E and Uguzzoni F, Stratified Lie Groups and Potential Theory for their Sub-Laplacians (2007) (Berlin, Heidelberg: Springer)
Bony J-M, Principle du maximum, inégalité de Harnack et unicité du probléme de Cauchy pour les opérateurs elliptiques dégénérés, Ann. Inst. Fourier Grenobles 19 (1969) 277–304
Brezis H and Nirenberg L, Positive solutions of nonlinear elliptic equations involving critical exponents, Comm. Pure Math. Appl. 36 (1983) 437–477
Brown K J and Wu T-F, A semilinear elliptic system involving nonlinear boundary condition and sign changing weight function, J. Math. Anal. Appl. 337 (2008) 1326–1336
Brown K J and Zhang Y, The Nehari manifold for a semilinear elliptic equation with a sign-changing weight function, J. Differential Equ. 193(2) (2003) 481–499
Danielli D, Garofalo N and Phuc N C, Hardy–Sobolev type inequalities with sharp constants in Carnot–Carathéodory spaces, Potential Anal. 34 (2011) 223–242
de Morais Filho D C and Souto M A S, Systems of \(p\)-Laplacian equations involving homogeneous nonlinearities with critical Sobolev exponent degrees, Comm. Partial Diff. Equ. 24(7–8) (1999) 1537–1553
Ferrari F and Franchi B, Harnack inequality for fractional sub-Laplacians in Carnot groups, Math. Z. 279 (2015) 435–458
Figueiredo D G, Gossez J P and Ubilla P, Local superlinearity and sublinearity for the \(p\)-Laplacian, J. Funct. Anal. 257 (2009) 721–752
Folland G B, Subelliptic estimates and function spaces on nilpotent Lie groups, Ark. Mat. 13 (1975) 161–207
Folland G B and Stein E M, Hardy Spaces on Homogeneous Groups, Volume 28 of Mathematical Notes (1982) (Princeton, NJ: Princeton University Press)
Garofalo N and Vassilev D, Regularity near the characteristic set in the non-linear Dirichlet problem and conformal geometry of sub-Laplacians on Carnot Groups, Math. Ann. 318 (2000) 453–516
Hamidi E I, Multiple solutions with changing sign energy to a nonlinear elliptic equation, Commun. Pure Appl. Anal. 3 (2004) 253–266
Hsu T-S, Multiple positive solutions for a critical quasilinear elliptic system with concave–convex nonlinearities, Nonlinear Anal. 71 (2009) 2688–2698
Kang D, Positive minimizers of the best constants and solutions to coupled critical quasilinear systems, J. Differ. Equ. 260 (2016) 133–148
Loiudice A, Semilinear subelliptic problems with critical growth on Carnot groups, Manuscript Math. 124 (2007) 247–259
Loiudice A, Critical growth problems with singular nonlinearities on Carnot groups, Nonlinear Anal. 126 (2015) 415–436
Loiudice A, Local behavior of solutions to sunelliptic problems with Hardy potential on Carnot groups, Mediterr. J. Math. 15 (2018) Art. No. 81
Loiudice A, Optimal decay of \(p\)-Sobolev extremals on Carnot groups, J. Math. Anal. Appl. 470 (2019) 619–631
Nyamoradi N, Existence and multiplicity of solutions to a singular elliptic system with critical Sobolev–Hardy exponents and concave-convex nonlinearities, J. Math. Anal. Appl. 396 (2012) 280–293
Peng S, Peng Y and Wang Z-Q, On elliptic systems with Sobolev critical growth, Calc. Var. (2016) 55, Art. No. 142
Ruzhansky M and Suragan D, Hardy inequalities on homogeneous groups (2019) (Birkhäuser, Cham)
Stein E M, Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals, Volume 43 of Princeton Mathematical Series (1993) (Princeton, NJ: Princeton University Press), with the assistance of Timothy S Murphy, Monographs in Harmonic Analysis, III
Vassilev D, Existence of solutions and regularity near the characteristic boundary for sub-Laplacian equation on Carnot Groups, Pacific J. Math 227(2) (2007) 361–397
Willem W, Minimax Theorems. Progress in Nonlinear Differential Equations and their Applications, vol. 24 (1996) (Boston, MA: Birkhäuser Boston Inc.)
Wu T-F, On semilinear elliptic equations involving concave-convex nonlinearities and sign changing weight function, J. Math. Anal. Appl. 318 (2006) 253–270
Zhang J, Sub-elliptic problems with multiple critical Sobolev–Hardy exponents on Carnot groups, Manuscript Math (2022) https://doi.org/10.1007/s00229-022-01406-x
Zhang J and Hsu T-S, Nonlocal elliptic systems involving critical Sobolev–Hardy exponents and concave–convex nonlinearities, Taiwanese J. Math. 23(6) (2019) 1479–1510
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by K Sandeep.
Rights and permissions
About this article
Cite this article
Zhang, J. Existence and multiplicity of positive solutions to sub-elliptic systems with multiple critical exponents on Carnot groups. Proc Math Sci 133, 10 (2023). https://doi.org/10.1007/s12044-023-00730-w
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12044-023-00730-w