Skip to main content
SpringerLink
Log in

Hamiltonian cycles in polyhedral maps

  • Published:
Proceedings - Mathematical Sciences Aims and scope Submit manuscript

Abstract

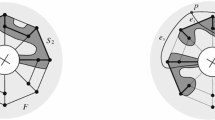
We present a necessary and sufficient condition for existence of a contractible, non-separating and non-contractible separating Hamiltonian cycle in the edge graph of polyhedral maps on surfaces. We also present algorithms to construct such cycles whenever it exists where one of them is linear time and another is exponential time algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Altshuler A, Construction and enumeration of regular maps on the torus, Discrete Math. 4 (1973) 201–217

  2. Archdeacon D, Topological graph theory: a survey (surveys in graph theory) (1995) (San Francisco, CA)

  3. Bondy J A and Murthy U S R, Graph theory with applications (1982) (North Holland, Amsterdam)

    Google Scholar 

  4. Brehm U and Schulte E, Polyhedral maps, Handbook of Discrete and Computational Geometry, edited by J E Goodman and J O Rourke (1997) (CRC Press) pp. 345–358

  5. Brunet R, Nakamoto A and Negami S, Every 5-connected triangulations of the Klein bottle is Hamiltonian, Yokohama Math. J. 47 (1999) 239–244

  6. Brunet R and Richter R B, Hamiltonicity of 5-connected toroidal triangulations. J. Graph Theory 20 (1995) 267–286

    Article  MathSciNet  MATH  Google Scholar 

  7. Cabello S, Verdière E C D, Lazarus F, Finding cycles with topological properties in embedded graphs. SIAM J. Discrete Math. 25 (2011) 1600–1614

    Article  MathSciNet  MATH  Google Scholar 

  8. Fujisawa J, Nakamoto A and Ozeki K, Hamilton cycles in bipartite toroidal graphs with a partite set of degree four vertices (preprint) http://www.fbc.keio.ac.jp/~fujisawa/papers.html

  9. Grünbaum B, Polytopes, graphs and complexes, Bull. Amer. Math. Soc. 76 (1970) 1131–1201

    Article  MathSciNet  MATH  Google Scholar 

  10. Kawarabayashi Ken-ichi and Ozeki K, Hamilton cycles in 4-connected troidal triangulations. Electronic Notes in Discrete Math. 38 (2011) 493–498

    Article  MATH  Google Scholar 

  11. Jennings D L G, Separating cycles in triangulations of the double torus, Ph.D. thesis (2003) (Vanderbilt University)

  12. Maity D and Upadhyay A K, Contractible Hamiltonian Cycles in Polyhedral Maps, Discrete Math. Algorithms Appl. 4 (2012)

  13. McMullen P and Schulte E, Abstract Regular Polytopes (2002) (CUP)

  14. Mohar B and Thomassen C, Graphs on Surfaces (2001) (The John Hopkins Univ. Press)

  15. Thomas R, and Yu X, Five-connected toroidal graphs are Hamiltonian. J. Combin. Theory Ser. B 69 (1997) 79–96

    Article  MathSciNet  MATH  Google Scholar 

  16. Tutte W T, A theorem on planar graphs, Trans. Amer. Math. Soc. 82 (1956) 99–116

    Article  MathSciNet  MATH  Google Scholar 

  17. Upadhyay A K, Contractible Hamiltonian Cycles in Triangulated Surfaces, Elemente der Mathematik 69 (1) 23–29

  18. Whitney H, A theorem on graphs, Ann. Math. 32 (1931) 378–390

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the anonymous referee whose comments led to a substantial improvement in the paper. The work of the second author is partially supported by SERB, DST Grant No. SR/S4/MS:717/10.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Patna, Bihta, Patna, 801 103, India

    Dipendu Maity & Ashish Kumar Upadhyay

Authors
  1. Dipendu Maity
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ashish Kumar Upadhyay
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dipendu Maity.

Additional information

Communicating Editor: Sharad S Sane

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maity, D., Upadhyay, A.K. Hamiltonian cycles in polyhedral maps. Proc Math Sci 127, 737–751 (2017). https://doi.org/10.1007/s12044-017-0356-1

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12044-017-0356-1

Keyword

Mathematics Subject Classification

Search

Navigation