Nonlinear stability and thermomechanical analysis of hydromagnetic Falkner–Skan Casson conjugate fluid flow over an angular–geometric surface based on Buongiorno’s model using homotopy analysis method and its extension

Abstract

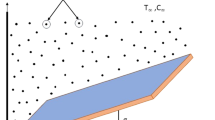
This paper aims to provide stability and thermomechanical analysis of hydromagnetic Falkner–Skan Casson conjugate fluid flow over an angular–geometric wedge-shaped surface. Based on the Buongiorno’s model, the governing boundary-layer equations are derived and solved iteratively using the homotopy analysis method (HAM). Furthermore, the HAM-series solution is optimised by minimising its squared residual errors. It is shown that the proposed approach can serve as an efficient criterion for accurately solving nonlinear problems.

Appendix A

The constitutive equation of the Bingham plastic model can be expressed as [14]

$$\begin{aligned} \left\{ {{\begin{array}{l} {{\begin{array}{l} {{{e}}_{ij} =0,\quad \dfrac{1}{2}\tau _{ij} \tau _{ji} \le P_y^2 ,} \\ \end{array} }} \\ {\tau _{ij} =2\left( {\mu _{\mathrm{B}} +\dfrac{P_y }{\sqrt{2\psi }}} \right) {e}_{ij} ,\quad \dfrac{1}{2}\tau _{ij} \tau _{ji} >P_y^2 .} \\ \end{array} }} \right. \end{aligned}$$

(A1)

It can be seen from eq. (A1), that the viscosity coefficient $\mu _{\mathrm{B}}$ diverges while the velocity gradient becomes zero (see [12]). It is noteworthy to mention that more details on the Bingham plastic model have also been reported in some previous studies (see [38,39,40]).