Abstract
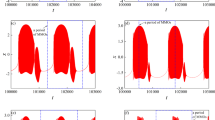
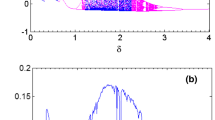
We report an investigation of the oscillation death (OD) of a parametrically excited coupled van der Pol–Mathieu (vdPM) system. The system can be considered as a pair of harmonically forced van der Pol oscillators under a double-well potential. The two oscillators are coupled with a cubic nonlinearity. We have shown that the system arrives at an OD regime when coupling strength crosses a threshold value at which the system undergoes saddle-node bifurcation and two limit cycles coalesce onto a fixed point of the system. We have further shown that this nonautonomous system possesses a centre manifold corresponding to the OD regime.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
A T Winfree, J. Theor. Biol. 16, 15 (1967)
M G Rosenblum and A S Pikovsky, Phys. Rev. Lett. 92, 114102 (2004)
S H Strogatz, Physica D 143, 1 (2000)
G B Ermentrout and N Kopell, SIAM J. Appl. Math. 50, 125 (1990)
K Konishi, Phys. Rev. E 68, 067202 (2003)
A Prasad, M Dhamala, N M Adhikari and R Ramaswamy, Phys. Rev. E 81, 027201 (2010)
Y Kuramoto, Chemical oscillations, waves, and turbulence (Dover, 2003)
K Bar-Eli, Physica D 14, 242 (1985)
D V Ramana Reddy, A Sen and G L Johnston, Phys. Rev. Lett. 80, 5109 (1998)
R Karnatak, R Ramaswamy and A Prasad, Phys. Rev. E 76, 035201(R) (2007)
A N Pisarchik, Phys. Lett. A 318, 65 (2003)
V Resmi, G Ambika and R E Amritkar, Phys. Rev. E 84, 046212 (2011)
V Resmi, G Ambika, R E Amritkar and G Rangarajan, Phys. Rev. E 85, 046211 (2012)
R Karnatak, N Punetha, A Prasad and R Ramaswamy, Phys. Rev. E 82, 046219 (2010)
A Prasad, S K Dana, R Karnatak, J Kurths and B Blasius et al, Chaos 18, 023111 (2008)
M Stich, A C Casal and J I Diaz, Phys. Rev. E 76, 036209 (2007)
H Sakaguchi and D Tanaka, Phys. Rev. E 76, 025201 (2007)
G Saxena, A Prasad and R Ramaswamy, Phys. Rep. 521, 205 (2012) and references therein.
A Pikovsky, M Rosenblum and J Kurths, Synchronization: A universal concept in nonlinear science (Cambridge, New York, 2001)
M P Bora and D Sarmah, Proceedings of the Fifth National Conference on Nonlinear Systems and Dynamics (Kolkota, 2009), http://ncnsd.org/proceedings/proceeding09/Paper/40.pdf
Y Saitou and T Honzawa, Proceedings of the International Congress on Plasma Physics and 25th EPS Conference on Fusion Plasma Physics (Prague, 1998)
M R Jana, A Sen and P K Kaw, Phys. Rev. E 48, 3930 (1993)
A N Pisarchick and B K Goswami, Phys. Rev. Lett. 84, 1423 (2000)
E J Doedel et al, AUTO 2000: Continuation and Bifurcation Software for Ordinary Differential Equations, http://indy.cs.concordia.ca/auto/
B Ermentrout, Simulating, analyzing, and animating dynamical systems: A guide to XPPAUT for researchers and students (Cambridge, 1987)
J Hale and H Koçak, Dynamics and bifurcations (Springer-Verlag, 1991)
J Guckenheimer and P Holmes, Nonlinear oscillations, dynamical systems, and bifurcations of vector fields (Springer-Verlag, New York, 1983)
J J S Vargas, J A Gonzalez, A Stefanovaska and P V E McClintock, Europhys. Lett. 85, 38008 (2009)
Y A Kuznetsov, Elements of applied bifurcation theory (Springer, 1998)
G H Goldstein, F Broner and S H Strogatz, SIAM J. Appl. Math. 57, 1163 (1997)
Mathematica website, http://www.wolfram.com/mathematica/
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
BORA, M.P., SARMAH, D. Oscillation death in a coupled van der Pol–Mathieu system. Pramana - J Phys 81, 677–690 (2013). https://doi.org/10.1007/s12043-013-0595-3
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12043-013-0595-3