On assessing the influence of a newly impounded reservoir on a nearby normal fault using a simple three-dimensional model of subsurface geological heterogeneity

Abstract

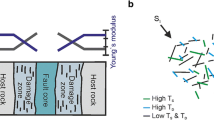
We assume that the subsurface at the site of a newly impounded reservoir has a small volume of rock with porous-elastic properties significantly different from those of the other rocks in the area. A normal fault passes through this rock volume. We adopt the following simplifications to quantify reservoir influence at different points of the fault in such a case. The reservoir is circular and of uniform depth. The small rock volume is spherical in shape and embedded in an otherwise homogeneous half space with values of porous-elastic properties in the range normally observed through laboratory measurements on rocks. We infer from calculated results that the reservoir will promote slip at low water level at points of the fault lying within the small rock volume if its diffusivity, and undrained and drained Poisson’s ratios are significantly lower than those of the other rocks at the site. The reservoir will promote slip on the normal fault at points outside the small rock volume at high water level.

Research highlights

• A 3D model for reservoir promoted slip on a subsurface normal fault at low water is investigated.

• The reservoir is circular. The fault cuts a porous-elastic (PE) sphere in a PE half-space.

• The fault slips at low water at points in the sphere if PE half-space has nominal properties.

• PE sphere has low diffusivity and low undrained and drained Poisson’s ratios.

Appendices

Appendix A

Estimation of the reservoir-induced destabilizing shear stress and stabilizing frictional stresses on a steeply dipping normal fault using the selected three-dimensional model of the subsurface

A1. Preliminaries

A1.1 Review: The following procedure has been evolved by us. Still, we recall for a perspective that a sphere or a spherical cavity has been considered in several earlier studies of elastic and porous-elastic media. Thus, to simulate elastic waves from a nuclear explosion, Thiruvenkatachar and Viswanathan (1965) investigated the dynamic response of an elastic half space to time dependent surface tractions acting on an embedded spherical cavity. Datta (1969) considered a rigid spherical inclusion in an elastic half space and obtained results for small vertical vibrations of the center of the sphere. The mathematical iterative approach was identical in both these articles.

Thermo-elastodynamic response of a spherical cavity in a saturated porous-elastic medium was investigated by Ganbi et al. (2010). He and Jin (2011) considered effects of a local heat source on the pore pressure and thermal stresses around a spherical cavity in a porous medium. Bai and Li (2013) examined the irreversible consolidation problem of a saturated porothermoelastic (sic) spherical body with a spherical cavity.

Our problem is intermediate between these two sets of sphere or spherical cavity problems. Consideration of a porous-elastic medium is more complex than consideration of a purely elastic medium, but consideration also of thermal effects in the porous-elastic medium is not necessary for our purpose.

A1.2. An approximation: Among the possible physical fields that may permeate a porous-elastic solid, our interest is in stress, displacement and pore pressure fields (SDPFs for short). Both the reservoir and the sphere exert influence on the SDPFs in the HS. In turn, the SDPFs in the sphere have contributions due to the reservoir as well as due to the presence of the sphere itself within the HS. Thiruvenkatachar and Viswanathan (1965) acknowledged that, in their case, the elastic stress and displacement fields in the elastic half space were influenced by the presence of the spherical cavity.

But we consider only those fields in the sphere and HS that are due to direct influence of the reservoir. In order to increase the precision of the numerical results obtained with this approximation, the radius of the sphere is kept small compared to the depth of its center and the radius of the reservoir.

A2. SDPFs referred to cylindrical coordinates

The elements of stress, displacement and pore pressure fields (SDPFs) in a PE solid using the cylindrical coordinate system of figure 1 are $\sigma _{zz}, \tau _{rz}, \sigma _{rr}, u_r, u_z$ and p. The following expressions for these SDPFs are taken from equations (9.47, 9.48, 9.42, 9.46 and 9.51) of Wang (2000). The expression for $\sigma _{rr}$ in equation (A1c) below was derived by us.

$$\begin{aligned} \sigma _{zz}(r,z) & =2G \int _0^\infty \bigg \{ \frac{k^2 \gamma c}{\iota \omega }(A_{1k} e^{mz}+A_{2k} e^{-mz}) \\& -(a_1 k z-a_4) A_{3k} e^{kz} \\&+ (a_1 kz+ a_4) A_{4k} e^{-kz}-k(A_{5k} e^{kz} \\&+ A_{6k} e^{-kz}) \bigg\}k J_0(kr) dk; \end{aligned}$$

(A1a)

$$\begin{aligned} \tau _{rz}(r,z) &= 2G \int _0^\infty \bigg\{ \frac{-km \gamma c}{\iota \omega }(A_{1k} e^{mz}-A_{2k} e^{-mz}) \\& +(a_1 kz-0.5) A_{3k} e^{kz}+ (a_1 kz+0.5) A_{4k} e^{-kz}\\&+k(A_{5k} e^{kz}-A_{6k} e^{-kz})\bigg\} kJ_1(kr)dk; \end{aligned}$$

(A1b)

$$\begin{aligned} \sigma _{rr}(r,z) & =2G\int _0^\infty \bigg \{ \left( \frac{k^2 \gamma c}{\iota \omega }- \gamma \right) (A_{1k} e^{mz}-A_{2k} e^{-mz}) \\& +a_1 (kz+2\nu _u) A_{3k} e^{kz}\\&+a_1(-kz+2\nu _u) A_{4k} e^{-kz}\\&+k(A_{5k} e^{kz}+A_{6k} e^{-kz})\bigg\} k J_0(kr)dk\\&-\frac{2G}{r} \int _0^\infty \bigg \{ \frac{k\gamma c}{\iota \omega } (A_{1k} e^{mz}+A_{2k} e^{-mz})\\&+a_1 z(A_{3k} e^{kz}- A_{4k} e^{-kz})\\&+A_{5k} e^{kz}+A_{6k} e^{-kz}\bigg\} kJ_1(kr)dk; \end{aligned}$$

(A1c)

$$\begin{aligned} u_r(r,z)=& \int _0^\infty \bigg\{ \frac{-k\gamma c}{\iota \omega } (A_{1k} e^{mz}+A_{2k} e^{-mz}) \\& +a_1 z(A_{3k} e^{kz}-A_{4k} e^{-kz})\\& +k(A_{5k} e^{kz}+A_{6k} e^{-kz})\bigg\} kJ_1(kr)dk;\end{aligned}$$

(A1d)

$$\begin{aligned} u_z(r,z)=& \int _0^\infty \bigg\{ \frac{m\gamma c}{\iota \omega } (A_{1k} e^{mz}-A_{2k} e^{-mz})\\& -(a_1 z-a_2/k) A_{3k} e^{kz}\\& - (a_1 z+a_2/k) A_{4k} e^{-kz}\\& -k(A_{5k} e^{kz}-A_{6k} e^{-kz})\bigg\} kJ_0(kr)dk; \end{aligned}$$

(A1e)

$$\begin{aligned} p_l(r,z) & = \, 2 \gamma G \int _0^\infty \bigg\{ a_5 (A_{1k} e^{mz}+A_{2k} e^{-mz})\\& -a_4 (A_{3k} e^{kz}+ A_{4k} e^{-kz})\bigg\} kJ_0(kr)dk; \end{aligned}$$

(A1f)

In these equations,

$$\begin{aligned} &a_1 =\, 1/(2(1-2\nu _u)); \\& a_2 =(3-4 \nu _u)a_1;\\& a_4= \, 2(1-\nu _u)a_1; \\& m=\sqrt{k^2+\iota \omega /c};\\& a_5= \, B(1-\nu )(1+\nu _u)/(3(\nu _u-\nu )); \\& \, \gamma\,= \, B(1+\nu _u)/(3(1-\nu _u)). \end{aligned}$$

Let $U_{iS}(r,z)$ and $U_{iH}(r,z),~i=1,\ldots,6,$ represent $\sigma _{zz}, \tau _{rz}, \sigma _{rr}, u_r, u_z$ and p in the sphere and the HS. Since each of the above equations contains the same six unknown constants $A_{jk}$ with different multiplying factors, therefore equations (A1a–A1f) for the sphere and the HS can be written compactly as follows:

$$\begin{aligned} U_{iS}(r,z) & = \int _0^\infty U_{iS}^{\prime} (k,r,z)dk,\quad (i=1,\ldots,6), \end{aligned}$$

(A2a)

$$\begin{aligned} U_{iH}(r,z) & = \int _0^\infty U_{iH}^{\prime} (k,r,z)dk, \quad(i=1,\ldots,6). \end{aligned}$$

(A2b)

The abbreviated expressions for the integrands are:

$$\begin{aligned} U_{iS}^{\prime} (k,r,z) & = \sum _{j=1}^6 \alpha _{ijS}^{\prime} (k,r,z) A_{jkS}, \quad (i = 1,\ldots, 6), \end{aligned}$$

(A3a)

$$\begin{aligned} U_{iH}^{\prime} (k,r,z) & = \sum _{j=2,4,6} \alpha _{ijH}^{\prime} (k,r,z) A_{jkH}, \quad (i = 1,\ldots,6). \end{aligned}$$

(A3b)

Only terms with negative exponentials are retained in the case of the HS to ensure finiteness of fields as z tends to infinity.

The coordinates (r, z) and $(R,\theta )$ for a given point in the space portrayed in figure 1 are related as follows:

$$\begin{aligned} r=R \sin \theta ; \quad z=z_0- R \cos \theta . \end{aligned}$$

Therefore, through these substitutions, we may write the above equations also as:

$$\begin{aligned} U_{iS}(R,\theta )= &{} \int _0^\infty U_{iS}^{\prime}(k,R,\theta )dk,\quad (i=1,\ldots,6), \end{aligned}$$

(A4a)

$$\begin{aligned} U_{iH}(R,\theta )= & {} \int _0^\infty U_{iH}^{\prime}(k,R,\theta )dk,\quad (i=1,\ldots,6). \end{aligned}$$

(A4b)

$$\begin{aligned} U_{iS}^{\prime}(k,R,\theta )= & {} \sum _{j=1}^6 \alpha _{ijS}^{\prime}(k,R,\theta ) A_{jkS}, \quad (i = 1,\ldots,6). \end{aligned}$$

(A5a)

$$\begin{aligned} U_{iH}^{\prime} (k,R,\theta )= & {} \sum _{j=2,4,6}\alpha _{ijH}^{\prime} (k,R,\theta ) A_{jkH}, \quad (i = 1,\ldots,6). \end{aligned}$$

(A5b)

A3. SDPF elements for spherical coordinates

The spherical elements $\sigma _{RR}, \tau _{R\theta }, u_\theta , u_R,$ p and ${\partial p}/{\partial R}$ of SDPFs are related to the above cylindrical elements for the sphere and the HS through the following equations.

$$\begin{aligned} \sigma _{RR}(R,\theta )= & {} U_1(R,\theta ) \cos ^2 \theta -U_2(R,\theta ) \sin 2\theta \\\quad + & {} U_3(R,\theta ) \sin ^2 \theta , \end{aligned}$$

(A6a)

$$\begin{aligned} \tau _{R\theta }(R,\theta ) & = \left[ U_1(R,\theta )-U_3(R,\theta ) \right] \sin \theta \cos \theta \\ & \quad + U_2(R,\theta ) \cos 2\theta , \end{aligned}$$

(A6b)

$$\begin{aligned} u_\theta (R,\theta )= & {} U_4(R,\theta ) \cos \theta +U_5(R,\theta ) \sin \theta , \end{aligned}$$

(A6c)

$$ \begin{aligned} u_R(R,\theta )= & {} U_4(R,\theta ) \sin \theta -U_5(R,\theta ) \cos \theta , \end{aligned}$$

(A6d)

$$\begin{aligned} p(R,\theta )= & {} U_6(R,\theta ). \end{aligned}$$

(A6e)

The quantity ${\partial p}/{\partial R}$ is obtained by straight forward differentiation of equation (A6e).

Let $V_{iS} (R,\theta )$ and $V_{iH} (R,\theta ), \quad(i=1,\ldots,6),$ represent $\sigma _{RR},\tau _{R\theta }, u_R, u_\theta , p$ and ${\partial p}/{\partial R}$ in the sphere and the HS. Then,

$$\begin{aligned} V_{iS}(R,\theta )= & {} \int _0^\infty V_{iS}^{\prime}(k,R,\theta )dk, \quad (i=1,\ldots,6), \end{aligned}$$

(A7a)

$$\begin{aligned} V_{iH}(R,\theta )= & {} \int _0^\infty V_{iH}^{\prime}(k,R,\theta )dk, \quad (i=1,\ldots,6). \end{aligned}$$

(A7b)

The integrands take the form:

$$\begin{aligned} V_{iS}^{\prime}(k, R,\theta )= & {} \sum _{j=1}^6 \beta _{ijS}^{\prime}(k,R,\theta ) A_{jkS}, \quad (i = 1,\ldots,6), \end{aligned}$$

(A8a)

$$\begin{aligned} V_{iH}^{\prime}(k,R,\theta )= & {} \sum _{j=2,4,6} \beta _{ijH}^{\prime}(k,R,\theta ) A_{jkH}, \quad (i = 1,\ldots,6). \end{aligned}$$

(A8b)

The $\beta _{ij}^{\prime}$’s for each j between 1 and 6 are obtained from the corresponding $\alpha _{ij}^{\prime}$’s using equations (A6a–A6e). We emphasize that the unknown constants $A_{jkS},~j=1,\ldots,6$ in equations (A3a, A5a and A8a) are the same respectively and the unknown constants $A_{jkH},~j=2,4,6$ in equations (A3b, A5b and A8b) are the same similarly. This is useful for solving the problem.

A4. Evaluation of unknown constants for the HS

Following the approximation stated in section A1.2 above, we proceed as if the HS is homogeneous. We consider that the top surface is pervious. Therefore, boundary conditions on $\sigma _{zzH}, \tau _{rzH}$ and $p_H$ are pertinent here. The following three equations are obtained from equations (A1a, A1b and A1f) by setting $z=0.$ In these equations, $J_1(R_R k)/(\pi R_R k)$ and $-J_1(R_R k)/(\pi R_R k)$ represent, in the k-domain, the vertical normal stress and pore pressure exerted on the surface of the HS by a uniform circular water reservoir of radius $R_R$ and unit total weight.

$$\begin{aligned} & 2G_H \left[ \frac{k^2 \gamma _H c_H}{\iota \omega } A_{2kH} + a_{4H} A_{4kH}-kA_{6kH}\right] =\frac{J_1(R_R k)}{\pi R_R k},\\& 2G_H \left[ \frac{k m_H \gamma _H c_H}{\iota \omega } A_{2kH} + 0.5 A_{4kH} - k A_{6kH}\right] =0,\\& 2\gamma _H G_H \left[ a_{5H} A_{2kH}- a_{4H}A_{4kH}\right] =-\frac{J_1(R_R k)}{\pi R_R k}. \end{aligned}$$

With $A_{jkH} ~(j=2,4,6),$ determined from the above equations, the right-hand sides of all the expressions in equations (A3b, A5b and A8b) can be evaluated.

A5. Evaluation of unknown constants for the sphere

A5.1 Boundary conditions on the surface of the sphere: The boundary conditions on the interface between the sphere and the HS are obtained from equations (A3a and A3b) with $R=R_S,$ where $R_S$ is the radius of the sphere:

$$\begin{aligned} V_{iS}(R_S,\theta )= V_{iH} (R_S,\theta ),\quad i=1,\ldots,6, \quad 0 \le \theta \le \pi . \end{aligned}$$

(A9a)

These conditions also hold for each k. Thus, from equations (A5a and A5b)

$$\begin{aligned} V_{ikS}^{\prime}(k,R_S,\theta )= V_{ikH}^{\prime}(k,R_S,\theta ),\quad i=1,\ldots,6, \quad 0 \le \theta \le \pi . \end{aligned}$$

(A9b)

These equations may be rewritten using equations (A8a) as:

$$\begin{aligned} \sum _{j=1}^6 \beta _{ijS}^{\prime} (k,R_S,\theta ) A_{jkS} =V_{ikH}^{\prime} (k,R_S,\theta ), \quad i=1,\ldots,6, \quad 0 \le \theta \le \pi . \end{aligned}$$

(A9c)

A5.2 Finite cosine transform: Use of finite cosine transform (FCT) technique is convenient to apply these point-wise conditions on the spherical boundary. Sneddon (1951, p72) gives the following relations for FCT and its inverse. If $0 \le \theta \le \pi$, then

$$\begin{aligned} f^{\prime}(n)= & {} \int _0^\pi f(\theta ) \cos n\theta ~d\theta , \end{aligned}$$

(A10a)

$$\begin{aligned} f(\theta )= & {} \frac{1}{\pi } f'(0)+ \frac{2}{\pi } \sum _{n=1}^\infty f'(n)\cos n\theta . \end{aligned}$$

(A10b)

A5.2.1 Use of FCT: Applying equation (A10a) on both sides of equations (A9c), we have:

$$\begin{aligned} \beta _{ijS}^{\prime \prime}(k,R_S,n)= & {} \int _0^\pi \beta _{ijS}^{\prime}(k,R_S,\theta ) \cos n\theta ~d\theta ,\quad i,j=1,\ldots,6,\,\,n= 0,\ldots,N, \end{aligned}$$

(B8a)

$$\begin{aligned} V_{iH}^{\prime \prime}(k,R_S,n)= & {} \int _0^\pi V_{iH}^{\prime} (k,R_S,\theta ) \cos n\theta ~d\theta ,~~i = 1,\ldots,6,\,\, n=0,\ldots,N. \end{aligned}$$

(B8b)

Thus, the equations (A9c) take the following form in the FCT domain.

$$\begin{aligned} \sum _{j=1}^6 \beta _{ijS}^{\prime \prime}(k,R_S,n) A_{jknS} =V_{iH}^{\prime \prime}(k,R_S,n),~~i = 1,\ldots,6,~~ n=0,\ldots,N. \end{aligned}$$

On solving these equations for each n in the range $n=0,\ldots,N,$ we obtain $N+1$ sets of values of the $A_{jknS},~j=1,\ldots,6$ for one value of k. The FCT integral are computed numerically.

A6. Determination of SDPFs at a point in the sphere

In order to compute reservoir influence at a point $(R, \theta )$ within the sphere, we obtain the following equivalents of equations (A5a) in the FCT domain:

$$\begin{aligned} U_{ikS}^{\prime \prime}(k, R_1, n)=\sum _{j=1}^6 \alpha _{ijS}^{\prime \prime}(k,R_1,n) A_{jknS}, \quad i=1,\ldots,6, \quad n=0,\ldots,N, \end{aligned}$$

$\alpha _{ijS}^{\prime \prime}(k,R_1,n)$ on the right-hand side can be computed. Therefore, using $A_{jknS}$’s determined in the section A5.4, the summands on the right-hand sides in these equations can be evaluated. Thus, the left-hand sides of these equations are evaluated also.

The inverse finite cosine transform defined in equation (A10b) then allows us to obtain for each $i=1,\ldots,6,$

$$\begin{aligned} U_{ikS}^{\prime}(k,R,\theta ) & \approx \frac{1}{\pi } U_{ikS}^{\prime \prime}(k,R,0) \\ &\quad + \frac{2}{\pi } \sum _{n=1}^N U_{ikS}^{\prime \prime}(k,R,n)\cos n \theta . \end{aligned}$$

The approximate equality symbol is used because the infinite series given in equation (A10a) has been curtailed to a N term series. The above entire procedure has to be repeated for suitably large number of values of k so that integrations with respect to k in equations (A5a) may be carried out numerically to obtain the values of $U_{iS}(R,\theta ).$

A7. Computation of $\tau _d$ and $\tau _f$

The expressions for $\tau _d$ and $\tau _f$ at a point $(R,\theta )$ on the fault within the sphere or the HS in terms of respective $U_i (R,\theta ),~i=1,\ldots,6$ are as follows.

$$\begin{aligned} \tau _d (R,\theta )= &\, {} \left[ U_1 (R,\theta )-U_3 (R,\theta ) \right] \sin \delta \cos \delta + U_2 (R,\theta ) \cos 2 \delta ;\\ \tau _f (R,\theta )= & \, {} \mu [\sigma (R,\theta )-U_6 (R,\theta )];~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\\ \sigma (R,\theta )= & \, {} U_1 (R,\theta ) \cos ^2 \delta -U_2 (R,\theta ) \sin 2 \delta +U_3 (R,\theta ) \sin ^2 \delta . \end{aligned}$$

A computer program was written for calculating $\tau _d$ and $\tau _f.$

Appendix B

The following abbreviations and symbols are used in the text and Appendix A for brevity and specificness.

moduli:

Porous-elastic moduli

sphere:

Porous-elastic sphere

FCT:

Finite cosine transform

HS:

Porous-elastic half space of the three-dimensional model

PE:

Porous-elastic

SDPFs:

Stress, displacement and pore pressure fields

U:

SDPFs $\sigma _{zz},~ \tau _{rz},$ etc.

V:

SDPFs $\sigma _{RR},~ \tau _{R\theta },$ etc.

c:

Hydraulic diffusivity

$\iota$:

Used with the imaginary parts of complex variables

k:

Hankel transform variable

n:

Finite cosine transform variable

p:

Pore pressure

r:

Radial coordinate in the cylindrical system

zz:

Coordinate in the cylindrical system

A:

Unknown constants to be determined from boundary conditions

B:

Skempton’s coefficient

G:

Shear Modulus

J:

Bessel Function

O:

Origin of a coordinate system

R:

Radial coordinate in the spherical system

$\alpha$:

Coefficient of A in equations (A3a, A3b, A5a, A5b)

$\beta$:

Coefficient of A in equations (A7a, A7b)

$\gamma$:

Loading efficiency

$\delta$:

Dip of fault plane

$\theta$:

Angle measure in the spherical system

$\mu$:

Coefficient of rock friction

$\nu$:

Poisson’s ratio

$\sigma$:

Normal stress

$\tau$:

Shear stress

$\omega$:

Angular frequency 

d:

Destabilizing stress

f:

Frictional stress

i:

Running index for $i=1,\ldots,6$

j:

Running index for $j=1,\ldots,6$

k:

Value in k domain

u:

Undrained Poisson’s ratio

H:

Variables in HS

S:

Variable in sphere 

$'$:

Hankel transform of the variable

$''$:

Finite cosine transform of the variable

$z_0$:

= 5000 m,

$R_R$:

= 1500 m,

$R_S$:

= 150 m,

$\mu$:

= 0.6,

$\omega$:

= 2 $\times 10^{-7}$ radians $\text{s}^{-1}$.