Skip to main content
SpringerLink
Log in

Analysis of thermal effect on propagation of Rayleigh surface waves in a composite structure

  • Published:
Journal of Earth System Science Aims and scope Submit manuscript

Abstract

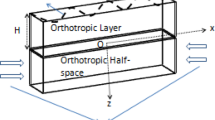
The present work deals with the propagation of Rayleigh surface wave in a self-reinforced thermoelastic layer lying over a dry sandy thermoelastic half-space. The expressions for thermal stresses and displacement components have been derived to characterize the dynamics of dry sandy materials. The dispersion equation of Rayleigh wave is obtained using concepts of potential function subjected to suitable boundary conditions. The obtained dispersion equation is complex in nature, so separating the real part of 6th order determinant expression, the dispersion equation of Rayleigh wave in the earth’s crust of sandy media is obtained and analyzed carefully. Some special cases are deduced to obtain the classical equation of Rayleigh wave that is well-consistent with the pre-established developed outcome. A numerical approach has been taken to express the theoretical result graphically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7

Similar content being viewed by others

References

  • Abd-Alla A M, Abo-Dahab S M and Hammad H A H 2011 Propagation of Rayleigh waves in a magneto thermoelasticorthotropic material under initial stress and gravity field; Appl. Math. Model 35 2981–3000.

    Article  Google Scholar 

  • Achenbach J D and Epstein H I 1967 Dynamic interaction of a layer and a half space; J. Eng. Mech. 93 27–42.

    Google Scholar 

  • Achenbach J D and Keshava S P 1967 Free waves in a plate supported by a semi infinite continuum; J. Appl. Mech. 34 397–404.

    Article  Google Scholar 

  • Belfield A J, Rogers T G and Spencer A J M 1983 Stress in elastic plates reinforced by fibres lying in concrete circles; J. Mech. Phys. Solids 31 25–54.

    Article  Google Scholar 

  • Biot M A 1956 Theory of propagation of elastic waves in a fluid-saturated porous solid; J. Acoust. Soc. Am. 28 168–178.

    Article  Google Scholar 

  • Biswas S 2018 Stroh analysis of Rayleigh waves in anisotropic thermoelastic medium; J. Therm. Stress. 41 627–644.

    Article  Google Scholar 

  • Biswas S 2020 Rayleigh waves in a nonlocal thermoelastic layer lying over a nonlocal thermoelastic half-space; Acta Mech. 231 4129–4144.

  • Biswas S 2021 Surface waves in piezothermoelastic transversely isotropic layer lying over piezothermoelastic transversely isotropic half-space; Acta Mech. 232 373–387.

  • Chirită S 2013 On the Rayleigh surface waves on an anisotropic homogeneous thermoelastic half space; Acta Mech. 224 657–674.

  • Destrade M 2007 Seismic Rayleigh waves in an exponentially graded orthotropic half space; Proc. R. Soc. A Math. Phys. 463 495–502.

    Google Scholar 

  • ElNaggar A M, Abd-Alla A M and Ahmed S M 1994 Rayleigh waves in magnetothermo microelastic half space under initial stress; Earth, Moon Planet. 45 175–185.

    Article  Google Scholar 

  • Gupta S, Ahmed M and Verma A K 2019 Analysis of Rayleigh waves in micropolar thermoelastic solid over a dual phase lag semi infinite thermoelastic substrate under inter-facial imperfections; Int. J. Geomech. 19 1–11.

    Article  Google Scholar 

  • Kar B K, Pal A K and Kalyani V K 2018 Propagation of Love waves in an irregular dry sandy layer; Acta Geol. Pol. 34 157–169.

    Google Scholar 

  • Lord H W and Shulman Y 1967 A generalized dynamical theory of thermoelasticity; J. Mech. Phys. Solids 15 209–309.

    Article  Google Scholar 

  • Markham M F 1970 Measurement of the elastic constants of fibre composites by ultrasonic; Composites 1 145–149.

    Article  Google Scholar 

  • Singh B, Kumari S and Singh J 2012 On Rayleigh wave in generalized magneto thermoelastic media with hydrostatic initial stress; Br. Pol. Acad. Sci.-Tech. 60 349–352.

    Google Scholar 

  • Weiskopf W H 1945 Stresses in solids under foundation; J. Franklin I 239 445–465.

    Article  Google Scholar 

Download references

Acknowledgement

Authors acknowledge the Council of Scientific and Industrial Research (CSIR) by the project (Grant Number 25(0296)/19/EMR-II) entitled ‘Mathematical Modeling of Elastic Waves in Fractional Order Thermoelastic Solids with Micro-configurations and Initially Stressed Media’ for providing financial support for this research work.

Author information

Authors and Affiliations

  1. Department of Mathematics and Computing, Indian Institute of Technology (Indian School of Mines), Dhanbad, India

    Shishir Gupta & Sandip Kumar Das

  2. Department of Finance, Xavier Institute of Social Service, Ranchi, India

    Rishi Dwivedi

  3. Department of Mathematics, Government Polytechnic, Patna, India

    Smita

  4. Department of Computer Science and Engineering, I.E.T. Dr. R.M.L. Avadh University, Ayodhya, Uttar Pradesh, India

    Piyush Rai

Authors
  1. Shishir Gupta
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rishi Dwivedi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Smita
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Piyush Rai
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Sandip Kumar Das
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Shishir Gupta: Conceptualization. Rishi Dwivedi: Validation and writing. Smita: Conceptualization, methodology, and original draft. Piyush Rai: Writing, review and editing. Sandeep Kumar Das: Methodology.

Corresponding author

Correspondence to Smita.

Additional information

Communicated by Anand Joshi

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gupta, S., Dwivedi, R., Smita et al. Analysis of thermal effect on propagation of Rayleigh surface waves in a composite structure. J Earth Syst Sci 131, 59 (2022). https://doi.org/10.1007/s12040-021-01802-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12040-021-01802-z

Keywords

Search

Navigation