SHYBRID: A Graphical Tool for Generating Hybrid Ground-Truth Spiking Data for Evaluating Spike Sorting Performance

Abstract

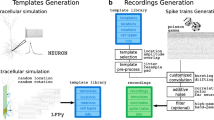
Spike sorting is the process of retrieving the spike times of individual neurons that are present in an extracellular neural recording. Over the last decades, many spike sorting algorithms have been published. In an effort to guide a user towards a specific spike sorting algorithm, given a specific recording setting (i.e., brain region and recording device), we provide an open-source graphical tool for the generation of hybrid ground-truth data in Python. Hybrid ground-truth data is a data-driven modelling paradigm in which spikes from a single unit are moved to a different location on the recording probe, thereby generating a virtual unit of which the spike times are known. The tool enables a user to efficiently generate hybrid ground-truth datasets and make informed decisions between spike sorting algorithms, fine-tune the algorithm parameters towards the used recording setting, or get a deeper understanding of those algorithms.

Appendix

A Auto hybridization fitting factor bounds

The calculation of the fitting factor bounds during the automatic hybridization is based on robust statistics, which are commonly used for the detection and removal of outliers. The automatic bounds selection is rather conservative, i.e., it is likely that quite a few good spikes are excluded from the hybridization when using the automated approach.

Consider ${\mathscr{B}}^{\left (n\right )} = \left \{\log _{10} \ {\upbeta }_{s}^{\left (n\right )} \ \vert \ s \in \mathcal {S}^{\left (n\right )} \right \}$ which is the set of the logarithm of the fitting factors (see “Hybrid Ground-Truth Model”) for a certain neuron n. The logarithm is used to be able to also remove close to zero fitting factors based on simple statistics. Given ${\mathscr{B}}^{\left (n\right )}$, the first and third quartile are calculated, denoted by Q₁ and Q₃ respectively. From those quartile values the interquartile range (IQR) is calculated as IQR = Q₃ −Q₁. From those statistics the bounds are calculated:

$$ l_{\beta}^{(n)} = 10^{\text{Q}_{1} - \frac{3}{4}\text{IQR}}, $$

(7)

and

$$ u_{\beta}^{(n)} = 10^{\text{Q}_{3} + \frac{3}{4}\text{IQR}}, $$

(8)

where the IQR scaling factor (i.e. $\frac {3}{4}$) was determined experimentally.

B Auto hybridization random unit relocation

During the automatic hybridization, a random unit relocation is calculated for every neuron. For this relocation, only a shift in the y-direction is considered. The random shift is determined by drawing a y-position on the probe grid model (see “Hybrid Ground-Truth Model”) from a discrete uniform distribution. This random y-position is the y-position to which the channel with the maximal deflection in the spike template is shifted to. In this way we avoid that the complete template is shifted off the probe. The actual shift can then be calculated as the random y-position minus the y-position of the channel with maximal deflection in the original template. A minimum shift of two channels is enforced, to make sure that the re-inserted unit is sufficiently separable from the original unit.

C External template import

When an external template is imported, there are no spike times available, neither is the scaling known. The spike occurrences are modeled as a poisson point process. The inter-spike interval Δ_ISI is then modelled by drawing from an exponential distribution:

$$ p({\Delta}_{\text{ISI}}, \lambda) = \lambda \exp\left( -\lambda {\Delta}_{\text{ISI}}\right), $$

(9)

where λ represents the desired spike rate. Every inter-spike interval sample $\hat {\Delta }_{\text {ISI}}$ is enforced to last at minimum the user-defined refractory period ${\Delta }_{\min \limits }$:

$$ \hat{\Delta}_{\text{ISI}} \leftarrow \max\left( \hat{\Delta}_{\text{ISI}}, {\Delta}_{\min}\right). $$

(10)

The actual simulated discrete spike times k_sim are obtained by calculating the cumulative sum over the inter-spike interval samples. Those spike times are then discretized by multiplying them with the recording sampling frequency and rounding each product to its nearest integer. This gives rise to a set of discrete spike times $\mathcal {S}^{\text {ext}} = \left \{ k_{\text {sim}} \right \}$.

The template scaling is derived from the user-defined desired peak-signal-to-noise ratio (PSNR $= 10\log _{10}\frac {P_{\text {peak}}}{P_{\text {noise}}}$). The scaling factor is calculated as follows:

$$ {\upbeta}^{\text{ext}} = \sqrt{\frac{P_{\text{noise}} 10^{\frac{\text{PSNR}}{10}} }{P_{\text{peak}}}}, $$

(11)

with P_peak equal to the square of the peak absolute value over all channels of the external template and P_noise equal to a robust estimate (based on the median absolute deviation) of the noise variance of the channel on which the template reaches its peak absolute value.

The hybrid data generated from an external template can then be described as follows:

$$ \begin{array}{@{}rcl@{}} &&\mathbf{h}^{\text{ext}}_{c}\left[k\right] = \mathbf{x}_{c}\left[k\right] + \\ &&\ \ \sum\limits_{s \in \mathcal{S}^{\text{ext}}} \sum\limits_{m = -K}^{K} \delta\left[k-(s+m)\right] {\upbeta}^{\text{ext}} \mathbf{t}_{c,\left( x,y\right)}^{\text{ext}}\left[m\right], \end{array} $$

(12)

where $\mathbf {t}_{c,\left (x,y\right )}^{\text {ext}}$ denotes the imported external template at channel c. Note that the template temporal window is derived from the external template directly. The external template is assumed to match the sampling frequency of the recording data that is being hybridized.

D Automatic merging

The merging framework for a specific ground-truth spike train consists of the following steps:

• 1) Compute the correspondence between the ground-truth spike train and all automatically recovered spike clusters in terms of precision and recall. More information on those performance metrics can be found in “Performance metrics calculation”.

• 2) Sort all clusters on descending precision, such that the cluster with the highest fraction of true spike times is on top of the list.

• 3) Merge the ordered clusters together in a top-down fashion, i.e. starting from the cluster with the highest precision, as long as the merge operation increases the F₁-score of the new cluster that contains all previously merged clusters.

Initially, the merging of clusters with a high precision will increase the sensitivity, at only a very small drop in precision. Such a merging will likely lead to an increase in F₁-score. At a certain point, clusters will start containing significant amounts of false positives that will notably decrease the precision of the merged cluster. This decrease will then result in a decreasing F₁-score. The proposed approach tries to find the combination of clusters with maximal F₁-score, without explicitly having to consider all possible combinations, preventing a combinatorial explosion from happening.