Abstract
The distribution of starches, proteins, and fat in baked foods determine their texture and palatability, and there is a great demand for techniques to visualize the distributions of these constituents. In this study, the distributions of gluten, starch, and butter in pie pastry were visualized without any staining, by using the fluorescence fingerprint (FF). The FF, also known as the excitation–emission matrix (EEM), is a set of fluorescence spectra acquired at consecutive excitation wavelengths. Fluorescence images of the sample were acquired with excitation and emission wavelengths in the ranges of 270–320 and 350–420 nm, respectively, at 10-nm increments. The FFs of each pixel were unmixed into the FFs and abundances of five constituents, gluten, starch, butter, ferulic acid, and the microscope slide, by using the least squares method coupled with constraints of non-negativity, full additivity, and quantum restraint on the abundances of the slide glass. The calculated abundances of butter, starch, and gluten at each pixel were converted to shades of red (R), green (G), and blue (B), respectively, and RGB images showing the distribution of these three constituents was composited. The composited images showed high correspondence with the images acquired with the conventional staining method. Furthermore, the ratio of gluten, starch, and butter in short pastry was calculated from the abundance images. The calculated ratio was 16.6:37.6:45.8, which was very close to the actual ratio of 12.7:38.8:48.5, and further proved the accuracy of this imaging method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Starches, proteins, and fat are important elements of the microstructure of baked foods (Cauvain and Young 2006). By changing the distribution of these three constituents, a broad range of foods with completely different textures can be produced, ranging from a soft brioche-type bread to a crispy pie. Because the microstructure of foods determines its texture, appearance, taste perception, and stability of the final product (Autio and Salmenkallio-Marttila 2001), developing techniques to study the microstructure of foods is very important.
However, visualizing the distribution of three or more constituents in microscale is difficult, especially in samples where the structure is easily destructed by procedures such as staining or substitution of water. Sowmya et al. (2009) and Watanabe et al. (2002) have observed the structure of cake crumbs and fat-containing dough, respectively, with scanning electron microscopy (SEM); however, they have reported that fat globules could not be observed with this method.
Confocal scanning lazar microscopy (CSLM) is a popular method to visualize the gluten and starch matrix in bread dough (Durrenberger et al. 2001; Lynch et al. 2009; Peighambardoust et al. 2006; Upadhyay et al. 2012). However, visualizing fat along with these two constituents is difficult. Li et al. (2004) have visualized fat and gluten proteins in bread dough using a combination of fluorescence stains and CSLM; however, the two components were stained and visualized separately. Moreno and Bouchon (2013) have also used CSLM to visualize the gluten matrix and absorbed oil in fried foods, although by incorporating fluorescence stains into the sample during the mixing process. Therefore, this method is not suitable for measuring actual products.
Although staining can be used to visualize specific constituents in a complex mixture (Autio and Salmenkallio-Marttila 2001, it becomes more difficult as the number of target constituents becomes larger. In addition, the results could markedly vary depending on the selection of stains and staining conditions such as concentration, solvent, and staining time.
Therefore, nondestructive methods that do not need a staining process have been developed. Hyperspectral imaging (HSI) is a technology that integrates conventional imaging and spectroscopy to obtain both spatial information and spectral information from a sample (Gowen et al. 2007). Hyperspectral images are composed of multiple wavebands for each spatial position of the target studies. Information such as the internal structure or the distribution of specific constituents can be obtained by analyzing the spectroscopic data. Another advantage of HSI, apart from its nondestructive quality, is that multiple constituents can be visualized from a single set of data, because a spectrum can provide information about multiple constituents.
Recently, studies have been performed using the fluorescence fingerprint (FF) as the spectroscopic data in HSI to visualize the distribution of gluten and starch in bread dough (Kokawa et al. 2011; Kokawa et al. 2012. The FF, also known as the excitation–emission matrix (EEM), is a set of fluorescence spectra acquired at consecutive excitation wavelengths, creating a three-dimensional diagram (Jiang et al. 2010. The pattern of this diagram is unique for every constituent, rather like a fingerprint. The FF has an advantage over conventional fluorescence spectra because it includes emission bands excited at many different excitation wavelengths, making it possible to make fine distinctions between constituents that differ only slightly in their fluorescence characteristics (Sikorska et al. 2008).
This study aims to visualize the distribution of fat, in addition to gluten and starch, using the FF in imaging. Pie pastry was chosen as the observation target. Pie pastry is made from wheat, water, and butter, and the fat is incorporated in relatively large clumps to provide the typical crunchy texture. There exist many types of pie pastries that differ in their structure and texture, depending on the manufacturing methods. We focused on two typical types of pie pastry, puff pastry and short pastry. Puff pastry is made by layering wheat flour dough and butter, so that when the butter melts in the baking process, the remaining dough forms thin crisp layers. On the other hand, short pastry is named after its “short” texture, which means that the food forms small crumbles in the mouth when bitten into. This is because the butter is mixed into the wheat flour, inhibiting the development of gluten.
Although these structures can be estimated from the manufacturing method, there are no studies that we know of which have actually visualized them. Therefore, the visualization of these structures would clearly show the strong link between the food structure and their known textures.
Materials and Methods
Sample Preparation
Two types of pie pastry were made, puff pastry and short pastry. Table 1 shows the composition of the ingredients for the two pastry doughs.
For the puff pastry, the first five ingredients were mixed in a dough mixer (Kenmix Aicoh Premier, KMM770, Kenwood Limited, Havant, United Kingdom) for 1 min at low speed and 6 min at medium speed. The temperature at the end of mixing was 23–24 °C. The total amount of flour used for the dough was 2,000 g, yielding dough of approximately 3,200 g. One thousand grams of the dough was rolled to a thickness of 3–4 cm and stored at 5 °C for 15–20 h. After resting, the dough was wrapped around 602 g of butter and rolled to a thickness of 5 mm with a sheeter. The dough sheet was folded in three, turned around 90°, and then folded in four. After a 30-min rest at −7 to −8 °C, the dough was folded in three, turned around 90°, and folded in three again (total 108 layers). After resting again at −7 to −8 °C for 30 min, the dough was rolled to a thickness of 2.5 mm.
For the short pastry, refrigerated butter was cut into approximately 1-cm3-sized pieces and mixed with the strong and weak types of flour and salt in a mixer (Kenmix Aicoh Premier, KMM770, Kenwood Limited) with a beating attachment until the butter particles were 2–3 mm in size. Water was added and the mixture was lightly kneaded into dough. The total amount of flour used for the short pastry was 1,000 g.
Gluten was extracted from the flour using the method by Macritchie (1985). Fractionation was performed with 50 g strong flour, 50 g weak flour, and 65 g of pure water. The flour used was taken from the same batches as those used for the pie pastry. The flour and water were cooled to 4 °C before mixing with a pin mixer (National MFG., Nebraska, USA) at 20 °C for 60 s. The dough temperature at the end of mixing was 18.1 °C. The dough was soaked in pure water for 60 min to strengthen the gluten connectivity and then kneaded with pure water to separate the insoluble protein fraction (gluten) from starch granules and other soluble substances. The bowl was cooled while washing off the starch granules, because it has been reported that the gluten yield is higher when the temperature is kept low (Macritchie 1985).
Both the pastry doughs and the extracted gluten were cut into approximately 1-cm3-sized pieces, embedded in a freeze embedding agent (3 % CMC embedding medium, iTec Science, Ibaraki, Japan) and frozen immediately in the cooling bath using hexane as the cooling medium in a cold trap (Eyela UT-2000, Tokyo Rikakikai Co. Ltd, Tokyo, Japan).
When the samples were completely frozen, they were sliced to 10-μm-thick slices using a cryotome (CM-1900, Leica) fixed with a Surgipath DH80HS blade (Leica). The thin slices were mounted on a slide glass (S-8215 and S-9901, Matsunami Glass Ind., Ltd., Osaka, Japan) and kept at −20 °C until observation.
FF Imaging System
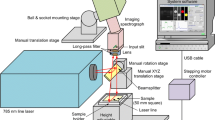
The FF imaging system was constructed as reported earlier (Kokawa et al. 2012; Kokawa et al. 2013b). The imaging system consisted mainly of a xenon lamp (MAX302, Asahi Spectra), two sets of band-pass filters (HQBP filter and M.C. filter, Asahi Spectra), and a monochrome charged coupled device (CCD) camera (ORCA-ER-1394, Hamamatsu Photonics, Shizuoka, Japan). The xenon lamp was equipped with a built-in UV mirror module, which restricted the wavelength range of light to a band of 250–385 nm. Light from the xenon lamp was transmitted through a band-pass filter to acquire the light of a specific wavelength, which was irradiated onto the sample through a rod lens (RLQL80-05, Asahi Spectra). Fluorescence from the sample was collected through an objective lens (NUV M Plan Apo, CVI Melles Griot Co., Ltd., Tokyo, Japan), transmitted through another band-pass filter, and the fluorescence image was acquired using the CCD camera. The two sets of band-pass filters were set in a filter wheel, and by rotating the wheel, fluorescence images of different excitation and emission wavelengths can be acquired.
The excitation and emission band-pass filters ranged from 270 to 330 nm and 350 to 420 nm, respectively, at 10-nm intervals. The excitation band-pass filters were coupled to two short-pass filters (XUVC260 and SU350, Asahi Spectra), which cut off unwanted light that passed through the band-pass filters. Fluorescence images of the sample were acquired at 53 combinations of the 7 excitation and 8 emission wavelengths. Three wavelength conditions (excitation/emission = 320/350, 330/350, 330/360) were omitted because the excitation and emission were close, causing reflective light to transmit. The 53 combinations of excitation and emission wavelengths make up the FF of this data. Therefore, the acquired dataset of 53 fluorescence images could also be viewed as the FFs of all the pixels in the image.
The imaging system was constructed on the top of an antivibration table (HMX-0605, Nippon Boushin Industry Co., Ltd., Shizuoka, Japan), and the sample was mounted on an XYZ-stage composed of a Z-axis motorized stage (MMU-60 V and QT-ADL1, Chuo Precision Industrial Co., Ltd, Tokyo, Japan) and a manual X–Y axis stage (Sigma Koki Co., Ltd, Tokyo, Japan). The Z-axis stage was essential to adjust the sample height to match the focal plane, which changed slightly for each emission wavelength.
The xenon lamp, filter wheels, Z-axis, and CCD camera were controlled from a personal computer using system development software (LabVIEW 8.2, National Instruments Corporation, Texas, USA).
Calibration of Imaging System
The lightning system (xenon lamp, UV mirror module, band-pass filters) and the observation system (objective lens, band-pass filters, CCD camera) were not constant regarding the wavelength of light, i.e., in some wavelengths the light was stronger or the CCD sensitivity was higher than in other wavelengths. In order to acquire an accurate FF of the sample, these distortions needed correcting.
The intensity of the excitation light was made uniform by adjusting the “light intensity (LI)” parameter of the xenon light source. The built-in mirror module allowed the LI to be adjusted from 5 to 100 % of the original intensity. The power of the light was measured with a power meter (NOVA2, Ophir Optronics Solutions Ltd., Jerusalem) for wavelengths of 260–330 nm and LI of 10–100 % (10 % intervals). Because the light power was lowest with light of 260 nm, the LI for the other wavelengths were adjusted to make them equal to the light power of 260 nm at LI 100 %.
The sensitivity of the observation system was made uniform by adjusting the exposure time of the camera. A white reflection standard (Spectralon SRM-99, LabSphere, Inc., New Hampshire, USA) was captured with the camera using emission filters from 350 to 420 nm. The white reflection standard shows over 99 % reflectance in the measured wavelength range. The white reflection standard image was acquired at exposure times of 10, 50, 100, and 500 ms, and the average luminance values of the images were plotted against the exposure times. Assuming a linear correlation between the exposure time and the luminance value, the relation between these parameters were calculated for each emission wavelength. Because 10 s was the longest exposure time available for the camera, the exposure time for the wavelength with the lowest sensitivity (350 nm) was set to 10 s. The exposure time for the other wavelengths was set to obtain the same luminance values as those obtained at 350 nm.
Acquisition of FF Images and Image Registration
The FF images of the two types of pie pastry and gluten were acquired using the imaging system described above. The fluorescence images were acquired in the order of the emission wavelength, with those of the combination of the longest emission and excitation wavelengths being the first. This was done to minimize the effect of UV radiation on the sample. The images were acquired with a binning of 2 × 2 (Nasibov et al. 2010) and saved as tagged image file format (tiff) images.
Dark image data were acquired in the same exposure times as the samples by turning off the light source and covering the objective lens with an aluminum foil. The dark images were subtracted from the corresponding fluorescence images to remove dark noise (Sugiyama 1999; Tsuta et al. 2002).
The fluorescence images acquired with the FF imaging system were imported into a computer and analyzed with versatile numerical analysis software (MATLAB R2012b, The MathWorks, Inc., MA, USA).
The fluorescence images needed position aligning because the images tended to slightly shift when the emission filter was changed (Kokawa et al. 2012), possibly due to color aberration of the optical system or a slight angle difference between each band-pass filter and the filter wheel. The fluorescence images were difficult to align because different constituents showed fluorescence depending on the emission wavelength. Therefore, an objective micrometer (NOB1, Sankei Co., ltd, Tokyo, Japan) was measured in advance using the same emission wavelengths. The shift between the emission wavelengths was calculated from the micrometer images and the fluorescence images of the samples were roughly aligned according to the calculated shift. Fine alignment was performed by using the image registration tool in MATLAB, which allowed the images to be aligned to an accuracy of one tenth of a pixel. The fringe parts that were out of view in some of the fluorescence images were deleted.
Spectral Unmixing
Spectral unmixing is a collective term for methods to decompose the observed spectra into a collection of constituent spectra, or endmembers, and a set of corresponding fractions, or abundances, which indicate the proportion of each endmember present in the pixel (Keshava and Mustard 2002). In this research, the endmembers would be the spectra of gluten, starch, and butter. Based on the preliminary analysis, the spectra of ferulic acid (fluorescent constituent contained in the wheat aleurone layer) and the microscope slide was added to the endmember library. By unmixing the FFs of each pixel in the pie pastry images, the content of these five constituents at each pixel can be calculated, and a distribution map for each constituent can be obtained.
Many spectral unmixing techniques based on the linear mixing model have been developed in recent decades (Boardman 1994; Keshava 2003; Nascimento and Bioucas Dias 2005a). The constrained least squares method was used in this study (Heinz and Chein 2001).
This method requires the endmembers to be known and assumes that the spectra of all the pixels in the sample can be expressed as a mixture of these endmembers. If appropriate endmembers can be acquired, least squares inversion is performed with two physical constraints, all abundances are equal to or larger than zero (nonnegativity), and the sum of the abundance fractions at one pixel is less than unity. This corresponds to solving the following problem:
in which the square of the Euclidean norm is minimized, and where y ∈ ℝL is the observed spectra, and D ∈ ℝL × M and α ∈ ℝL are the endmember and abundance matrices, respectively. L is the number of combinations of excitation and emission wavelengths, and M is the number of endmembers. This can be formulated as
where \( \mathrm{G}=\left[\begin{array}{c}\hfill -\mathbf{I}\hfill \\ {}\hfill {1}^{\mathrm{T}}\hfill \end{array}\right]\ \left(\mathbf{I}\in {\mathrm{\mathbb{R}}}^{M\times M},\ 1\in {\mathrm{\mathbb{R}}}^M\right) \) and \( \mathrm{h}={\left[\begin{array}{cc}\hfill {0}^{\mathrm{T}}\hfill & \hfill 1\hfill \end{array}\right]}^{\mathrm{T}}\left(0\in {\mathrm{\mathbb{R}}}^M\right) \). This is solved by optimization methods for quadratic programming, such as active-set (Gill et al. 1984) and interior-point (Gondzio 1997) methods.
In this study, an additional constraint was applied to the abundances of the microscope slide to be either 0 (the slide is covered with the sample) or 1 (there is no sample on the slide). This quantum restraint on the abundances of the microscope slide altered formula (1) to
where U(x) is a step function that is expressed as
The second term is added only to the slide data. This optimization becomes the following minimization:
where b ∈ ℝM is unity for b slide and zero for other components, and C = bb T. In order to solve this problem, formula (1) (without quantum regularization) was optimized first, followed by either of the problems in (5) depending on the α i value first obtained by the optimization of (1).
Because the abundances can be calculated unambiguously from the endmembers, choosing them is an important step. The endmember spectra of gluten, starch, butter, ferulic acid, and microscope slide were calculated by the following methods.
Gluten and ferulic acid show characteristic FFs, and therefore, the endmember spectra were extractable from the pie pastry data by an unsupervised extraction method, vertex component analysis (VCA) (Nascimento and Bioucas Dias 2005b). VCA extracts the candidates for endmembers by projecting the data onto the subspaces determined by dimensionality reduction algorithms and choosing the vertices of the data group. The candidate endmember FFs were compared to the FFs of the extracted gluten and manually selected aleurone fragments in the pie pastry, and the candidate with the largest cosine similarity was chosen as the endmember of gluten and ferulic acid, respectively.
Starch, butter, and the microscope slide show only weak fluorescence and their endmember FFs needed to be chosen manually. Small areas corresponding to starch granules and air holes in the pie pastry image were selected for the starch and microscope slide, respectively. For the butter, the butter layer area in the puff pastry was used. The FFs of all the pixels in the selected area were averaged to obtain the endmember spectra.
Results and Discussions
Endmember FFs
Figure 1 shows the endmember FFs of gluten, starch, butter, ferulic acid, and the microscope slide. Gluten shows the typical fluorescence pattern of aromatic amino acids, mainly tryptophan, which has a peak at excitation and emission wavelengths of 280 and 350 nm, respectively (Schulman 1985).
The fluorescence of ferulic acid in the aleurone layers of wheat kernel has been indicated by others (Irving et al. 1989). Ferulic acid has a fluorescence peak at excitation and emission wavelengths of 350 and 430 nm, respectively. Although this wavelength combination is beyond the measurement range used in this study, it is possible to observe the fluorescence band in the longer wavelengths of the FF.
The microscope slide shows weak fluorescence with peak intensity at excitation and emission wavelengths of 320 and 380 nm, respectively. This fluorescence could be due to some chemical treatment on the surface of the microscope slide, or alternately, because of weak reflected or diffused light (where the exCitation and emission wavelengths are equal) that has passed through the band-pass filters. The ideal band-pass filter completely cuts out light outside the designed wavelength band; however, the actual filters may pass a small fraction of light at other wavelengths. As a result, a small portion of the light transmitted through the excitation band-pass filter may directly pass thorough the emission band-pass filter after being reflected by the microscope slide. The latter explanation is convincing, because the same fluorescence pattern can be observed with higher intensities in the FFs of starch and butter.
Starch and butter show fluorescence patterns that seem like the combination of microscope slide fluorescence and aromatic amino acids. Amylose and amylopectin in starch are not fluorescent, but starch granules are known to have a thin protein membrane on their surface (Yoshino et al. 2005) and this may the reason for the fluorescence peak similar to that of gluten. Butter is known to contain fluorophors such as carotenoids; fluorescence from these constituents can be measured with a fluorescence spectrophotometer if the sample is thick enough (approximately 2 mm thickness). This fluorescence becomes very weak when the sample is thinly sliced and is hardly detectable with the FF imaging system. However, a slight difference between the FFs of starch and butter at emission wavelength of 420 nm, which enables the discrimination of the two constituents, may be due to carotenoids.
Since the FFs of starch and butter are similar to the linear combination of the FFs of microscope slide and aromatic amino acids, the normal constrained least squares algorithm unmixes the FF of a pixel containing a pure constituent into the FFs of several other constituents. Figure 2 shows preliminary results suffering from this problem. Starch is distributed “thinly” over the areas shown with red arrows, which is unrealistic because starch exists in granular form. As shown in later results, this area corresponds to the microscope slide, but the FFs of microscope slide were incorrectly unmixed into starch and butter.
Abundance images acquired in preliminary calculations. Abundance images of a starch, c butter, and e microscope slide in short pastry. The grayscale corresponds to an abundance of 1.0 (white) to 0.0 (black). The scale bar shows 100 μm. In areas shown with red arrows, starch exists in “thin layers,” which is unrealistic since starch exists in granular form
Visualization by the Constrained Least Squares Method with the Quantum Restraint
The quantum restraint was applied to the abundances of microscope slide to overcome the problem explained above. Figure 3 shows the abundance images of ferulic acid, butter, starch, gluten, and the microscope slide in the short pastry, acquired by unmixing the FFs with the quantum restraint on the microscope slide. Abundances for the microscope slide are shown in black (abundance = 0.0) and white (abundance = 1.0), and those for the other constituents are shown in continuous values between 0.0 and 1.0. Compared to Fig. 2, the constituents are clearly separated from each other, and the abundance image of starch shows granular features. Figure 4 shows the abundance images of the same constituents in the puff pastry. The image shows a band of butter sandwiched between two layers of the wheat dough.
Abundance images calculated with the quantum restraint (short pastry). Abundance images of a gluten, b starch, c butter, d ferulic acid, and e microscope slide in short pastry. The grayscale corresponds to an abundance of 1.0 (white) to 0.0 (black). The scale bar shows 100 μm. Compared to Fig. 2, the starch is shown in sharp granular form and there is a clear distinction between the microscope slide and sample
Abundance images calculated with the quantum restraint (puff pastry). Abundance images of a gluten, b starch, c butter, d ferulic acid, and e microscope slide in short pastry. The grayscale corresponds to an abundance of 1.0 (white) to 0.0 (black). The scale bar shows 100 μm. The layer of butter is sandwiched between two layers of dough
The two sets of images show distinct differences between the structures of the short and puff pastry. Apart from the obvious difference in the distribution of butter (mixed into the wheat dough or existing in layers), there is a large difference in the morphology of gluten. The gluten in the short pastry is observed in small and large clumps, whereas those in the puff pastry form a net-like structure, spread in the direction of dough extension (parallel to the layers of the dough and butter). The net-like structure of gluten in the puff pastry is presumed to be due to the mixing of dough (6 min at the medium speed) in the absence of fat. On the other hand, the flour for the short pastry is directly mixed to fat, which is known to inhibit the formation of gluten (Figoni 2008). The small clumps of gluten in the short pastry are presumably aggregations of the protein fraction existing in the flour particles.
The size distributions of the microscope slide areas are also very different. The short pastry shows many large voids compared to the small airspaces seen in the puff pastry. The puff pastry is rolled many times during its preparation, which would eliminate large voids. Consequently, the short pastry is mixed only roughly, which leaves or even incorporates air in the dough.
The texture of puff pastry is expressed as “flakiness,” referring to the number of layers in the baked product (Figoni 2008). The development of gluten structure with good extensibility is critical in achieving this “flakiness,” since the dough layers need to stay intact during the baking process to trap in the steam that puffs up the pastry (Cauvain and Young 2006). On the other hand, short pastry are characterized by their “tenderness” or “shortness” which is achieved by lubricating gluten proteins with fat and preventing them from hydrating and forming structure (Figoni 2008; Ghotra et al. 2002). With either manufacturing method, the optimum distribution of the gluten proteins and fat is the key to achieving the desired texture. The abundance images of gluten and butter clearly show these distributions.
Furthermore, the distribution of ferulic acid which is contained in the aleurone layers of wheat kernel could become critical when working with whole wheat flour, which contains more traces of the aleurone and pericarp than white flour. Although there are no reports on the structure of pie pastry made with whole wheat that we know of, Autio (2006)) have reported that solids from the germ and aleurone layer prevent gluten formation and gas cell structure both physically and chemically. Gluten formation is an important factor in wheat products, and methods to visualize gluten and other constituents simultaneously, and without any staining would contribute greatly to the research on cereal foods.
Image Composition and Validation by Stained Image
In order to validate the analysis results, both the samples were stained with a dual stain method, which stains gluten and fat in blue and orange, respectively. Figure 5 shows the composite image of the puff pastry with butter, starch, and gluten abundances shown in red, green, and blue, respectively, and the corresponding stained image.
Comparison of the image calculated from the fluorescence fingerprint (FF) data and the stained image (puff pastry) a Composite image of the abundance images of butter (red), starch (green), and gluten (blue) in puff pastry, and b stained image of the same sample. Protein is stained blue and fat is stained orange. The scale bar shows 100 μm
The red band of butter is visualized distinctly in both the images, and some large starch granules can also be distinguished in both the images. The gluten strands running in the horizontal direction can also be seen in the stained image.
Figure 6 shows the composite image of the short pastry with butter, starch, and gluten abundances shown in red, green, and blue, respectively and the corresponding stained image.
Comparison of the image calculated from the fluorescence fingerprint (FF) data and the stained image (short pastry) a Composite image of the abundance images of butter (red), starch (green), and gluten (blue) in short pastry, and b stained image of the same sample. Protein is stained blue and fat is stained orange. The scale bar shows 100 μm
In both the FF and stained images, large aggregates of gluten can be observed. The positions of the starch granules and fat in the analyzed image largely correspond with those of the stained image. Although the FFs of butter and starch were difficult to distinguish by visual judgment, it was possible to accurately obtain their abundances.
Compared to the stained image, the FF image seems to show a large quantity of butter. Therefore, the total quantity of gluten, starch, and butter calculated from the abundance image was compared to the value calculated from the ratio of the ingredients used for the pastry.
In the short pastry, 85 g of butter was mixed to 141 g of wheat flour dough. Around 20 % of the wheat flour dough is gluten, and the rest, starch (Kokawa et al. 2013a). This means that the weight ratio of gluten, starch, and flour is 12:50:38. Because the fluorescence intensity would be proportional to the volume of these constituents, the specific gravity of 1.1, 1.5, and 0.91 for gluten, starch, and butter, respectively, was used to convert the weight ratio to volume ratio. This afforded a volume ratio of 13.1:38.5:48.4 for gluten, starch, and butter.
In contrast, the ratio calculated from the abundance matrix was 16.6:37.6:45.8 for gluten, starch, and butter. This is very close to the ratio calculated from the ingredients of the pie pasty, and seems to support the accuracy of the imaging method.
Conclusions
In this study, FF imaging was combined with spectral unmixing methods to visualize the distribution of three constituents: gluten, starch, and butter. As a result, it was possible to visualize two more constituents: ferulic acid and the microscope slide. The results of this study are very significant because they indicate that a broad range of constituents, even those that show low levels of fluorescence such as starch and butter, can be visualized with FF imaging, if the right constraints are applied.
Imaging with autofluorescence is seemingly restricted compared to near-infrared (NIR) or infrared (IR) imaging because only fluorescent samples can be visualized with autofluorescence. However, this study showed that many constituents that are categorized to be measured by vibrational information (measured by NIR and IR), such as starch and fat, can actually be measured by fluorescence.
References
Autio, K. (2006). Effects of cell wall components on the functionality of wheat gluten. Biotechnology Advances, 24(6), 633–635.
Autio, K., & Salmenkallio-Marttila, M. (2001). Light microscopic investigations of cereal grains, doughs and breads. Lebensmittel-Wissenschaft Und-Technologie-Food Science and Technology, 34(1), 18–22.
Boardman, J. W. (1994). Geometric mixture analysis of imaging spectrometry data, Geoscience and Remote Sensing Symposium, 1994. IGARSS ‘94. Surface and Atmospheric Remote Sensing: Technologies, Data Analysis and Interpretation International, 4, 2369–2371.
Cauvain, S. P., & Young, L. S. (2006). Baked products: science, technology and practice. Oxford: Blackwell Publishing Ltd.
Durrenberger, M. B., Handschin, S., Conde-Petit, B., & Escher, F. (2001). Visualization of food structure by confocal laser scanning microscopy (CLSM). Lebensmittel-Wissenschaft Und-Technologie-Food Science and Technology, 34(1), 11–17.
Figoni, P. (2008). How baking works: exploring the fundamentals of baking science (2nd ed.). New Jersey: Wiley.
Ghotra, B. S., Dyal, S. D., & Narine, S. S. (2002). Lipid shortenings: a review. Food Research International, 35(10), 1015–1048.
Gill, P. E., Murray, W., Saunders, M. A., & Wright, M. H. (1984). Procedures for optimization problems with a mixture of bounds and general linear constraints. ACM Transactions of Mathematical Software, 10(3), 282–298.
Gondzio, J. (1997). Presolve analysis of linear programs prior to applying an interior point method. INFORMS Journal on Computing, 9(s1), 73–91.
Gowen, A. A., O’Donnell, C. P., Cullen, P. J., Downey, G., & Frias, J. M. (2007). Hyperspectral imaging—an emerging process analytical tool for food quality and safety control. Trends in Food Science & Technology, 18(12), 590–598.
Heinz, D. C., & Chein, I. C. (2001). Fully constrained least squares linear spectral mixture analysis method for material quantification in hyperspectral imagery. IEEE Transactions on Geoscience and Remote Sensing, 39(3), 529–545.
Irving, D. W., Fulcher, R. G., Bean, M. M., & Saunders, R. M. (1989). Differentiation of wheat based on fluorescence, hardness, and protein. Cereal Chemistry, 66(6), 471–477.
Jiang, J. K., Wu, J., & Liu, X. H. (2010). Fluorescence properties of lake water. Spectroscopy and Spectral Analysis, 30(6), 1525–1529.
Keshava, N. (2003). A survey of spectral unmixing algorithms. Lincoln Laboratory Journal, 14(1), 55–78.
Keshava, N., & Mustard, J. F. (2002). Spectral unmixing. IEEE Signal Processing Magazine, 19(1), 44–57.
Kokawa, M., Fujita, K., Sugiyama, J., Tsuta, M., Shibata, M., Araki, T., et al. (2011). Visualization of gluten and starch distributions in dough by fluorescence fingerprint imaging. Bioscience Biotechnology and Biochemistry, 75(11), 2112–2118.
Kokawa, M., Fujita, K., Sugiyama, J., Tsuta, M., Shibata, M., Araki, T., et al. (2012). Quantification of the distributions of gluten, starch and air bubbles in dough at different mixing stages by fluorescence fingerprint imaging. Journal of Cereal Science, 55(1), 15–21.
Kokawa, M., Sugiyama, J., Tsuta, M., Yoshimura, M., Fujita, K., Shibata, M., et al. (2013a). Fluorescence fingerprint imaging of gluten and starch in wheat flour dough with consideration of total constituent ratio. Food Science and Technology Research, 19(6), 933–938.
Kokawa, M., Sugiyama, J., Tsuta, M., Yoshimura, M., Fujita, K., Shibata, M., et al. (2013b). Development of a quantitative visualization technique for gluten in dough using fluorescence fingerprint imaging. Food and Bioprocess Technology, 6(11), 3113–3123.
Li, W., Dobraszczyk, B. J., & Wilde, P. J. (2004). Surface properties and locations of gluten proteins and lipids revealed using confocal scanning laser microscopy in bread dough. Journal of Cereal Science, 39(3), 403–411.
Lynch, E. J., Dal Bello, F., Sheehan, E. M., Cashman, K. D., & Arendt, E. K. (2009). Fundamental studies on the reduction of salt on dough and bread characteristics. Food Research International, 42(7), 885–891.
Macritchie, F. (1985). Studies of the methodology for fractionation and reconstitution of wheat flours. Journal of Cereal Science, 3(3), 221–230.
Moreno, M. C., & Bouchon, P. (2013). Microstructural characterization of deep-fat fried formulated products using confocal scanning laser microscopy and a non-invasive double staining procedure. Journal of Food Engineering, 118(2), 238–246.
Nascimento, J. M. P., & Bioucas Dias, J. M. (2005a). Does independent component analysis play a role in unmixing hyperspectral data? IEEE Transactions on Geoscience and Remote Sensing, 43(1), 175–187.
Nascimento, J. M. P., & Bioucas Dias, J. M. (2005b). Vertex component analysis: a fast algorithm to unmix hyperspectral data. IEEE Transactions on Geoscience and Remote Sensing, 43(4), 898–910.
Nasibov, H., Kholmatov, A., Akselli, B., Nasibov, A., & Baytaroglu, S. (2010). Performance analysis of the CCD pixel binning option in particle-image velocimetry measurements. IEEE/ASME Transactions on Mechatronics, 15(4), 527–540.
Peighambardoust, S. H., van der Goot, A. J., van Vliet, T., Hamer, R. J., & Boom, R. M. (2006). Microstructure formation and rheological behaviour of dough under simple shear flow. Journal of Cereal Science, 43(2), 183–197.
Schulman, S. G. (1985). Molecular luminescence spectroscopy methods and applications: part 1. New York: Wiley.
Sikorska, E., Glisuzynska-Swiglo, A., Insinska-Rak, M., Khmelinskii, I., De Keukeleire, D., & Sikorski, M. (2008). Simultaneous analysis of riboflavin and aromatic amino acids in beer using fluorescence and multivariate calibration methods. Analytica Chimica Acta, 613(2), 207–217.
Sowmya, M., Jeyarani, T., Jyotsna, R., & Indrani, D. (2009). Effect of replacement of fat with sesame oil and additives on rheological, microstructural, quality characteristics and fatty acid profile of cakes. Food Hydrocolloids, 23(7), 1827–1836.
Sugiyama, J. (1999). Visualization of sugar content in the flesh of a melon by near-infrared imaging. Journal of Agricultural and Food Chemistry, 47(7), 2715–2718.
Tsuta, M., Sugiyama, J., & Sagara, Y. (2002). Near-infrared imaging spectroscopy based on sugar absorption band for melons. Journal of Agricultural and Food Chemistry, 50(1), 48–52.
Upadhyay, R., Ghosal, D., & Mehra, A. (2012). Characterization of bread dough: rheological properties and microstructure. Journal of Food Engineering, 109(1), 104–113.
Watanabe, A., Larsson, H., & Eliasson, A. C. (2002). Effect of physical state of nonpolar lipids on rheology and microstructure of gluten-starch and wheat flour doughs. Cereal Chemistry, 79(2), 203–209.
Yoshino, Y., Hayashi, M., & Seguchi, M. (2005). Presence and amounts of starch granule surface proteins in various starches. Cereal Chemistry, 82(6), 739–742.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Kokawa, M., Yokoya, N., Ashida, H. et al. Visualization of Gluten, Starch, and Butter in Pie Pastry by Fluorescence Fingerprint Imaging. Food Bioprocess Technol 8, 409–419 (2015). https://doi.org/10.1007/s11947-014-1410-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11947-014-1410-y