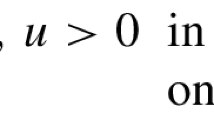Abstract
In this paper, we consider the following problem involving fractional Laplacian with a Hardy potential operator
where \(\Omega \) is a smooth bounded domain in \({\mathbb {R}}^{N}\) which contains the origin, \(\mu \ge 0\), \(\lambda >0\), \(0<\alpha <1\), \(1< q < 2\), \(2_{\alpha }^{*}=\frac{2 N}{N-2 \alpha }\) and \((-\Delta )^{\alpha }\) is the spectral fractional Laplacian. Using an approximate argument, some local Pohozaev Identities, Fountain Theorem and its Dual version, we prove that the above problem has two disjoint and infinite sets of solutions under suitable conditions on N, q and \(\mu \).
Similar content being viewed by others
Data availability
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Bartsch, T.: Infinitely many solutions of a symmetric Dirichlet problem. Nonlinear Anal. 20, 1205–1216 (1993)
Bartsch, T., Willem, M.: On an elliptic equation with concave and convex nonlinearities. Proc. Am. Math. Soc. 123, 3555–3561 (1995)
Brandle, C., Colorado, E., de Pablo, A., Sanchez, U.: A concave-convex elliptic problem involving the fractional Laplacian. Proc. R. Soc. Edinb. A Math. 143, 39–71 (2013)
Caffarelli, L., Silvestre, L.: An extension problem related to the fractional Laplacian. Commun. Partial Differ. Equ. 32(7–9), 1245–260 (2007)
Cao, D.M., Peng, S.J., Yan, S.S.: Infinitely many solutions for p-Laplacian equation involving critical Sobolev growth. J. Funct. Anal. 262, 2861–2902 (2012)
Cao, D., Yan, S.: Infinitely many solutions for an elliptic problem involving critical Sobolev growth and Hardy potential. Calc. Var. Partial Differ. Equ. 38, 471–501 (2010)
Devillanova, G., Solimini, S.: Concentration estimates and multiple solutions to elliptic problems at critical growth. Adv. Differ. Equ. 7(10), 1257–1280 (2002)
Di Nezza, E., Palatucci, G., Valdinoci, E.: Hitchhiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136, 521–573 (2011)
Echarghaoui, R., Khouakhi, M., Masmodi, M.: Existence and multiplicity of positive solutions for a class of critical fractional Laplacian systems. J. Elliptic Parabol. Equ. (2022). https://doi.org/10.1007/s41808-022-00177-6
Echarghaoui, R., Masmodi, M.: Two disjoint and infinite sets of solutions for a concave-convex critical fractional Laplacian equation. Fract. Calc. Appl. Anal. 25, 1604–1629 (2022). https://doi.org/10.1007/s13540-022-00060-0
Fabes, E., Kenig, C.E., Serapioni, R.P.: The local regularity of solutions of degenerate elliptic equations. Commun. Stat. Theory Methods 7(1), 77–116 (1982)
Fall, M.M.: Semilinear elliptic equations for the fractional Laplacian with Hardy potential. Nonlinear Anal. 193, 111311 (2020)
Frank, R.L., Lieb, E.H., Seiringer, R.: Hardy–Lieb–Thirring inequalities for fractional Schrödinger operators. J. Am. Math. Soc. 21, 924–950 (2008)
Herbst, I.W.: Spectral theory of the operator \( (p^2+m^2)^{1/2}-Ze^2/r\). Commun. Math. Phys. 53, 285–294 (1977)
Landkof, N.S.: Foundations of Modern Potential Theory. Springer, Berlin (1972)
Molica Bisci, G., Radulescu, V., Servadei, R.: Variational Methods For Nonlocal Fractional Problems. Cambridge University Press, Cambridge (2015)
Stinga, P., Torrea, J.: Extension problem and Harnack’s inequality for some fractional operators. Commun. Partial Differ. Equ. 35, 2092–2122 (2010)
Thin, N.V.: Nontrivial solutions of some fractional problems. Nonlinear Anal. 38, 146–170 (2017)
Trudinger, N.S.: Remarks concerning the conformal deformation of Riemannian structures on compact manifolds. Ann. Sc. Norm. Super. Pisa Cl. Sci. 3(22), 265–274 (1968)
Yafaev, D.: Sharp constants in the Hardy–Rellich inequalities. J. Funct. Anal. 168, 121–144 (1999)
Yan, S., Yang, J., Yu, X.: Equations involving fractional Laplacian operator: compactness and applications. J. Funct. Anal. 269(1), 47–79 (2015)
Wang, C., Yang, J., Zhou, J.: Solutions for a nonlocal problem involving a Hardy potential and critical growth. JAMA 144, 261–303 (2021)
Willem, M.: Minimax Theorems. Birkhäuser, Boston (1996)
Funding
The authors did not receive support from any organization for the submitted work.
Author information
Authors and Affiliations
Contributions
all authors contributed equally to this work.
Corresponding author
Ethics declarations
Ethical approval
This article does not contain any studies with human participants or animals performed by any of the authors.
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Echarghaoui, R., Khouakhi, M. & Masmodi, M. Two disjoint and infinite sets of solutions for a nonlocal problem involving a Hardy potential and critical growth with concave nonlinearities. J. Pseudo-Differ. Oper. Appl. 14, 56 (2023). https://doi.org/10.1007/s11868-023-00548-0
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11868-023-00548-0
Keywords
- Hardy–Sobolev fractional Laplacian
- Critical elliptic problem
- Compactness
- Infinitely many solutions
- Fountain Theorem
- Concave–convex nonlinearities