Skip to main content
SpringerLink
Log in

Type of mathematical proof: personal preference or adaptive teaching behavior?

  • Original Article
  • Published:
ZDM Aims and scope Submit manuscript

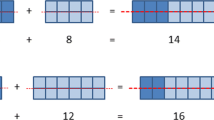
Abstract

In our study, 32 German and Swiss 8th/9th-grade classes of lower-secondary school worked with their teacher on the same proving problem. The sample belongs to the Swiss-German study “Quality of Instruction, Learning Behavior and Mathematical Understanding”. Our data analyses relate to the teachers’ approaches to generating a specific form of evidence with their classes when dealing with a particular elementary number-theory problem. We address the question of how the different strategies can be characterized as manifestations of a certain approach to proving and try to clarify in which way the observed approach can be interpreted as adaptive teaching behavior. For this purpose, we searched for possible correlations between three main strategies or types of generating a specific form of evidence (experimental, operative, formal-deductive approach) on the one hand and (a) the teachers’ beliefs and personal characteristics and (b) the students’ prior knowledge of algebra and mathematics in general on the other hand. As our analyses show, three main approaches to proving occurred but not in equal proportions: there is a predominance of the approach that entails the highest extent of formalization and abstraction. Nevertheless, an operative way of proving is widespread too. On the whole, the findings indicate that one particular approach to proving can be interpreted as a personal preference of a specific group of teachers and, at the same time, with respect to the students’ mathematical skills as a manifestation of adaptive teaching behavior.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Notes

  1. De Villiers (1990) describes the following five functions of proofs: verification, explanation, systematization, discovery, and communication.

  2. In the education systems of Germany and Switzerland, lower-secondary education (grades 7 to 9) is organized in a streamed model. Depending on their academic achievements, students are assigned to one of three different school types (or tracks) that differ in their demands.

  3. The survey of the teachers confirmed this assumption: the teachers reported that they often (four-point scale: 1: never, 2: rarely, 3: often, 4: very often) base the planning of their mathematics lessons on the learning-related preconditions of the students in the class (M = 3.38; SD = 0.61; N = 32) and on the results of the previous lesson (M = 3.56; SD = 0.50; N = 32).

  4. In one class, the students first solved the problem in small-group work and thereafter presented their solutions in a whole-class discussion. In all other classes, the predominant pattern consisted in classroom discourse in which the teacher and the students jointly dealt with the problem.

  5. ‘Prototypical mathematics teachers’ are teachers who teach (more or less) exclusively mathematics and (nearly) no other subjects while ‘all-rounders’ are teachers who teach a range of different subjects in parallel (e.g., mathematics, biology, chemistry, physics, and computer science).

References

  • Aberdein, A. (2009). Mathematics and argumentation. Foundation of Science, 14(1), 1–8. https://doi.org/10.1007/s10699-008-9158-3.

    Article  Google Scholar 

  • Aebli, H. (1981). Denken. Das Ordnen des Tuns. Stuttgart: Klett-Cotta.

    Google Scholar 

  • Ainsworth, S. (1999). The functions of multiple representations. Computers and Education, 33(2/3), 131–152.

    Article  Google Scholar 

  • Ainsworth, S., Bibby, P., & Wood, D. (2002). Examining the effects of different multiple representational systems in learning primary mathematics. Journal of the Learning Sciences, 11(1), 25–61.

    Article  Google Scholar 

  • Arzarello, F., Olivero, F., Paola, D., & Robutti, O. (2007). The transition to formal proof in geometry. In P. Boero (Ed.), Theorems in school. From history, epistemology and cognition to classroom practice (pp. 305–323). Rotterdam: Sense.

    Chapter  Google Scholar 

  • Balacheff, N. (1988). Etude des processus de preuve chez des élèves de collège. Grenoble: Université Joseph Fournier.

    Google Scholar 

  • Balacheff, N. (2010). Bridging knowing and proving in mathematics: A didactical perspective. In G. Hanna, H. N. Jahnke & H. Pulte (Eds.), Explanation and proof in mathematics (pp. 115–135). New York: Springer.

    Chapter  Google Scholar 

  • Baroody, A. J., & Dowker (Eds.). (2003). The development of arithmetic concepts and skills: Constructing adaptive expertise. Mahwah: Erlbaum.

    Google Scholar 

  • Bieg, M., Goetz, T., Wolter, I., & Hall, N. C. (2015). Gender stereotype endorsement differentially predicts girls’ and boys’ trait-state discrepancy in math anxiety. Frontiers in Psychology, 17(6), 1404. https://doi.org/10.3389/fpsyg.2015.01404.

    Article  Google Scholar 

  • Blömeke, S., & Kaiser, G. (2014). Theoretical framework, study design and main results of TEDS-M. In S. Blömeke, F.-J. Hsieh, G. Kaiser & W. H. Schmidt (Eds.), International perspectives on teacher knowledge, beliefs and opportunities to learn. TEDS-M results (pp. 19–48). Heidelberg: Springer.

    Chapter  Google Scholar 

  • Brunner, E. (2013). Innermathematisches Beweisen und Argumentieren in der Sekundarstufe I. Münster: Waxmann.

    Google Scholar 

  • Brunner, E., Jullier, R., & Lampart, J. (2019). Aufgabenangebot zum mathematischen Begründen in je zwei aktuellen Mathematikbüchern für die fünfte bzw. achte Klasse (in prep.).

  • Common Core State Standards Initiative. (2012). Mathematics standards. http://www.corestandards.org/Math. Accessed 10 March 2018.

  • Corno, L., & Snow, R. E. (1986). Adapting teaching to individual differences among learners. In M. C. Wittrock (Ed.), Handbook of research on teaching (pp. 605–629). New York: Macmillan.

    Google Scholar 

  • de Villiers, M. (1990). The role and the function of proof in mathematics. Pythagoras, 24, 17–24.

    Google Scholar 

  • de Villiers, M. (2010). Experimentation and proof in mathematics. In G. Hanna, H. N. Jahnke & H. Pulte (Eds.), Explanation and proof in mathematics (pp. 205–221). Dodrecht: Springer.

    Chapter  Google Scholar 

  • D-EDK. (2014). Lehrplan 21. Mathematik. Bern: Projekt Lehrplan 21.

    Google Scholar 

  • Dreyfus, T., Nardi, E., & Leikin, R. (2012). Forms of proof and proving in the classroom. In G. Hanna & M. de Villiers (Eds.), Proof and proving in mathematics education: The 19th ICMI study (pp. 191–213). Dodrecht: Springer.

    Google Scholar 

  • Drüke-Noe, C. (2014). Aufgabenkultur in Klassenarbeiten im Fach Mathematik. Empirische Untersuchungen in neunten und zehnten Klassen. Wiesbaden: Springer.

    Book  Google Scholar 

  • Duncker, K. (1935). Zur Psychologie des produktiven Denkens. Berlin: Springer.

    Google Scholar 

  • Duval, R. (2007). Cognitive functioning and the understanding of mathematical processes of proof. In P. Boero (Ed.), Theorems in school (pp. 137–161). Rotterdam: Sense.

    Google Scholar 

  • Fischbein, E. (1982). Intuition and proof. For the Learning of Mathematics, 3(2), 9–18.

    Google Scholar 

  • Furinghetti, F., & Morselli, F. (2011). Beliefs and beyond: Hows and whys in the teaching of proof. ZDM, 43(4), 587–599.

    Article  Google Scholar 

  • Hammer, S., Reiss, K., Lehner, M. C., Heine, J.-H., Sälzer, C., & Heinze, A. (2016). Mathematische Kompetenz in PISA 2015: Ergebnisse, Veränderungen und Perspektiven. In K. Reiss, C. Sälzer, A. Schiepe-Tiska, E. Klieme, & O. Köller (Eds.), PISA 2015. Eine Studie zwischen Kontinuität und Innovation (pp. 219–247). Münster: Waxmann.

    Google Scholar 

  • Hanna, G. (1990). Some pedagogical aspects of proof. Interchange, 21(1), 6–13.

    Article  Google Scholar 

  • Hanna, G., & Barbeau, E. (2008). Proofs as bearers of mathematical knowledge. ZDM, 40(3), 345–353.

    Article  Google Scholar 

  • Hanna, G., & Barbeau, E. (2010). Proofs as bearers of mathematical knowledge. In G. Hanna, H. N. Jahnke & H. Pulte (Eds.), Explanation and proof in mathematics (pp. 85–100). Dodrecht: Springer.

    Chapter  Google Scholar 

  • Hanna, G., & Jahnke, H. N. (1996). Proof and proving. In A. Bishop, K. Clements, C. Keitel, J. Kilpatrick & C. Laborde (Eds.), International handbook of mathematics education (pp. 877–908). Dodrecht: Kluwer.

    Google Scholar 

  • Harel, G., & Sowder, L. (1998). Students’ proof schemes: Results from exploratory studies. CBMS Issues in Mathematics Education, 7, 234–283.

    Article  Google Scholar 

  • Healy, L., & Hoyles, C. (2000). A study of proof conceptions in algebra. Journal for Research in Mathematics Education, 31(4), 396–428.

    Article  Google Scholar 

  • Heintz, B. (2000). Die Innenwelt der Mathematik. Zur Kultur und Praxis einer beweisenden Disziplin. Vienna: Springer.

    Book  Google Scholar 

  • Heinze, A., Star, J. R., & Verschaffel, L. (2009). Flexible and adaptive use of strategies and representations in mathematics education. ZDM, 41(5), 535–540.

    Article  Google Scholar 

  • Hiebert, J., Carpenter, T. P., Fennema, E., Fuson, K. C., Wearne, D., Murray, H., Olivier, A., & Human, P. (1997). Making sense. Teaching and learning mathematics with understanding. Portsmouth: Heinemann.

    Google Scholar 

  • Hiebert, J., Gallimore, R., Garnier, H., Givvin, K. B., Hollingsworth, H., & Jacobs, J. (2003). Teaching mathematics in seven countries. Results from the TIMSS 1999 video study. Washington, DC: U.S. Department of Education, Institute of Education Sciences.

    Book  Google Scholar 

  • Hugener, I., Pauli, C., Reusser, K., Lipowsky, F., Rakoczy, K., & Klieme, E. (2009). Teaching patterns and learning quality in Swiss and German mathematics lessons. Learning and Instruction, 19(1), 66–78.

    Article  Google Scholar 

  • Jahnke, H. N. (2008). Theorems that admit exceptions, including a remark on Toulmin. ZDM, 40(3), 363–371.

    Article  Google Scholar 

  • Jahnke, H. N., & Ufer, S. (2015). Argumentieren und Beweisen. In R. Bruder, L. Hefendehl-Hebeker, B. Schmidt-Thieme & H.-G. Weigand (Eds.), Handbuch der Mathematikdidaktik (pp. 331–355). Heidelberg: Springer Spektrum.

    Google Scholar 

  • Klieme, E., Pauli, C., & Reusser, K. (Eds.). (2006). Dokumentation der Erhebungs- und Auswertungsinstrumente zur schweizerisch-deutschen Videostudie “Unterrichtsqualität, Lernverhalten und mathematisches Verständnis”. Videoanalysen. Frankfurt: DIPF.

    Google Scholar 

  • Klieme, E., Pauli, C., & Reusser, K. (2009). The Pythagoras Study. In T. Janik & T. Seidel (Eds.), The power of video studies in investigating teaching and learning in the classroom (pp. 137–160). Münster: Waxmann.

    Google Scholar 

  • KMK. (2005). Bildungsstandards der Kultusministerkonferenz. Erläuterungen zur Konzeption und Entwicklung. Munich: Luchterhand.

    Google Scholar 

  • Knuth, E. (2002). Teachers’ conceptions of proof in the context of secondary school mathematics. Journal of Mathematics Teacher Education, 33(5), 61–82.

    Article  Google Scholar 

  • Kotelawa, U. (2009). A survey of teacher beliefs on proving. In F.-L. Lin, F.-J. Hsieh, G. Hanna, & M. de Villiers (Eds.), Proof and proving in mathematics education. ICMI Study 19 Conference Proceedings (Vol. 1, pp. 250–255). Taipei: The Department of Mathematics, National Taiwan Normal University.

    Google Scholar 

  • Lipowsky, F., Drollinger-Vetter, B., Hartig, J., & Klieme, E. (2006). Dokumentation der Erhebungs- und Auswertungsinstrumente zur schweizerisch-deutschen Videostudie “Unterrichtsqualität, Lernverhalten und mathematisches Verständnis” (Vol. 14). Frankfurt: DIPF. Leistungstests (Materialien zur Bildungsforschung.

    Google Scholar 

  • Lorenz, J. H. (2017). Einige Anmerkungen zur Repräsentation von Wissen über Zahlen. JMD, 38(1), 125–139.

    Article  Google Scholar 

  • Malek, A., & Movshovitz-Hadar, N. (2011). The effect of using transparent pseudo-proofs in linear algebra. RME, 13(1), 33–58.

    Google Scholar 

  • Mason, J., & Pimm, D. (1984). Generic examples: Seeing the general in the particular. Educational Studies in Mathematics, 15, 277–289.

    Article  Google Scholar 

  • Muijs, D., & Reynolds, D. (2002). Teachers’ beliefs and behaviors: What really matters? Journal of Classroom Interaction, 37, 3–15.

    Google Scholar 

  • NCTM (Ed.). (2000). Principles and standards for school mathematics. Reston: NCTM.

    Google Scholar 

  • Newell, A., & Simon, H. (1972). Human problem solving. Englewood Cliffs: Prentice-Hall.

    Google Scholar 

  • OECD (Ed.). (2016). PISA 2015 results: Excellence and equity in education (Vol. 1). Paris: OECD.

    Book  Google Scholar 

  • Pfeiffer, K. (2011). Features and purposes of mathematical proofs in the view of novice students: Observations from proof validation and evaluation performances. Galway: National University of Ireland.

    Google Scholar 

  • Rakoczy, K., Buff, A., & Lipowsky, F. (2005). Befragungsinstrumente. In E. Klieme, C. Pauli & K. Reusser (Eds.), Dokumentation der Erhebungs- und Auswertungsinstrumente zur schweizerisch-deutschen Videostudie “Unterrichtsqualität, Lernverhalten und mathematisches Verständnis” (Vol. 1). Frankfurt: DIPF.

    Google Scholar 

  • Reid, D. (2005). The meaning of proof in mathematics education. In M. Bosch (Ed.), European research in mathematics education IV. Proceedings of CERME 4, San Feliu de Guixols, Spain. Barcelona: University Ramon Llull.

    Google Scholar 

  • Reid, D. A., & Knipping, C. (2010). Proof in mathematics education. Research, learning and teaching. Rotterdam: Sense.

    Book  Google Scholar 

  • Reusser, K. (1984). Problemlösen in wissenstheoretischer Sicht. Problematisches Wissen, Problemformulierung und Problemverständnis. Berne: University of Berne.

    Google Scholar 

  • Reusser, K. (1993). Tutoring systems and pedagogical theory: Representational tools for understanding, planning, and reflection in problem solving. In S. P. Lajoie & S. J. Derry (Eds.), Computers as cognitive tools (pp. 143–177). Hillsdale: Erlbaum.

    Google Scholar 

  • Reuterswärd, E., & Hemmi, K. (2011). Upper secondary school teachers’ views of proof and the relevance of proof in teaching mathematics. In M. Pytlak, T. Rowland & E. Swoboda (Eds.), Proceedings of the seventh congress of the European Society for Research in Mathematics Education (pp. 253–262). Rzeszów: University of Rzeszów.

    Google Scholar 

  • Rowland, T. (2002). Generic proofs in number theory. In S. R. Campbell & R. Zazkis (Eds.), Learning and teaching number theory (pp. 157–183). Westport: Ablex.

    Google Scholar 

  • Schoenfeld, A. (1992). Learning to think mathematically: Problem solving, metacognition, and sense-making in mathematics. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). New York: Macmillan.

    Google Scholar 

  • Spiro, R. J., & Jehng, J. C. (1990). Cognitive flexibility and hypertext: Theory and technology for the nonlinear and multidimensional traversal of complex subject matter. In D. Nix & R. Spiro (Eds.), Cognition, education, and multimedia: Exploring ideas in high technology (pp. 163–205). Hillsdale: Erlbaum.

    Google Scholar 

  • Staub, F. C., & Stern, E. (2002). The nature of teachers’ pedagogical content beliefs matters for students’ achievement gains: Quasi-experimental evidence from elementary mathematics. Journal of Educational Psychology, 94(2), 344–355.

    Article  Google Scholar 

  • Stipek, D. J., Givvin, K. B., Salmon, J. M., & MacGyvers, V. L. (2001). Teachers’ beliefs and practices related to mathematics instruction. Teaching and Teacher Education, 17, 213–226.

    Article  Google Scholar 

  • Stylianides, G. L. (2008). An analytic framework of reasoning and proving. For the Learning of Mathematics, 28(1), 9–16.

    Google Scholar 

  • Thompson, D. R., Senk, S. L., & Johnson, G. J. (2012). Opportunities to learn reasoning and proof in high school mathematics textbooks. Journal for Research in Mathematics Education, 43(3), 253–295.

    Article  Google Scholar 

  • Vygotsky, L. S. (1978). Mind in society. Cambridge: Harvard University Press.

    Google Scholar 

  • Wagenschein, M. (1968). Verstehen lehren. Genetisch-Sokratisch-Exemplarisch. Weinheim: Beltz.

    Google Scholar 

  • Warner, L. B., Schorr, R. Y., & Davis, G. E. (2009). Flexible use of symbolic tools for problem solving, generalization, and explanation. ZDM, 41(5), 663–679.

    Article  Google Scholar 

  • Wertheimer, M. (1964). Produktives Denken (2nd ed.). Frankfurt: Kramer.

    Google Scholar 

  • Wittmann, E. C., & Müller, N. G. (1988). Wann ist ein Beweis ein Beweis? In P. Bender (Ed.), Mathematikdidaktik—Theorie und Praxis. Festschrift für Heinrich Winter (pp. 237–258). Berlin: Cornelsen.

    Google Scholar 

  • Wittmann, E. Ch. (2009). Operative proof in elementary mathematics. In F.-L. Lin, F.-J. Hsieh, G. Hanna, & M. De Villiers (Eds.), Proof and proving in mathematics education. ICMI Study 19 Conference Proceedings (pp. 251–256). Taipei: Department of Mathematics National Taiwan Normal University.

    Google Scholar 

  • Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation and autonomy in mathematics. The Journal of Research in Mathematics Education, 27, 458–477.

    Article  Google Scholar 

Download references

Acknowledgements

We thank the Swiss National Science Foundation (SNSF) for supporting the project.

Author information

Authors and Affiliations

  1. Thurgau University of Teacher Education, Unterer Schulweg 3, 8280, Kreuzlingen, Switzerland

    Esther Brunner

  2. Institute of Education, University of Zurich, Zurich, Switzerland

    Kurt Reusser

Authors
  1. Esther Brunner
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kurt Reusser
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Esther Brunner.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Brunner, E., Reusser, K. Type of mathematical proof: personal preference or adaptive teaching behavior?. ZDM Mathematics Education 51, 747–758 (2019). https://doi.org/10.1007/s11858-019-01026-y

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11858-019-01026-y

Keywords

Mathematics Subject Classification

Search

Navigation