Skip to main content
SpringerLink
Log in

Discrete Bethe-Sommerfeld conjecture for triangular, square, and hexagonal lattices

  • Published:
Journal d'Analyse Mathématique Aims and scope

Abstract

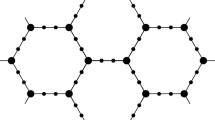
We prove the discrete Bethe-Sommerfeld conjecture on the graphene lattice, on its dual lattice (the triangular lattice), and on the extended Harper lattice. For each of these lattice geometries, we analyze the behavior of small periodic potentials. In particular, we provide sharp bounds on the number of gaps that may perturbatively open, we describe sharp arithmetic criteria on the periods that ensure that no gaps open, and we characterize those energies at which gaps may open in the perturbative regime. In all three cases, we provide examples that open the maximal number of gaps and estimate the scaling behavior of the gap lengths as the coupling constant goes to zero.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. Avila, S. Jitomirskaya and C. Marx, Spectral theory of extended Harper’s model and a question by Erdős and Szekeres, Invent. Math. 210 (2017), 283–339.

    Article  MathSciNet  Google Scholar 

  2. S. Becker and M. Zworski, Magnetic oscillations in a model of graphene, Comm. Math. Phys. 367 (2019), 941–989.

    Article  MathSciNet  Google Scholar 

  3. S. Becker, R. Han and S. Jitomirskaya, Cantor spectrum of graphene in magnetic fields, Invent. Math. 218 (2019), 979–1041.

    Article  MathSciNet  Google Scholar 

  4. J. Bellissard and B. Simon, Cantor spectrum for the almost Mathieu equation, J. Funct. Anal. 48 (1982), 408–419.

    Article  MathSciNet  Google Scholar 

  5. G. Berkolaiko and A. Comech, Symmetry and Dirac points in graphene spectrum, J. Spectr. Theory 8 (2018), 1099–1148.

    Article  MathSciNet  Google Scholar 

  6. A. Brouwer and W. Haemers, Spectra of Graphs, Springer, New York, 2012.

    Book  Google Scholar 

  7. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. Geim, The electronic properties of graphene, Rev. Mod. Phys. 81 (2009), 109–162.

    Article  Google Scholar 

  8. F. Chung, Spectral Graph Theory, American Mathematical Society, Providence, RI, 1997.

    MATH  Google Scholar 

  9. D. Cvetković, M. Doob, I. Gutman and A. Torĝasev, Recent Results in the Theory of Graph Spectra, Elsevier, Amsterdam, 1988.

    MATH  Google Scholar 

  10. D. Cvetković, M. Doob and H. Sachs, Spectra of Graphs, J. A. Barth, Heidelberg, 1995.

    MATH  Google Scholar 

  11. P. Delplace and G. Montambaux, WKB analysis of edge states in graphene in a strong magnetic field, Phys. Rev. B 82 (2010), 205412.

    Article  Google Scholar 

  12. M. Embree and J. Fillman, Spectra of discrete two-dimensional periodic Schrödinger operators with small potentials, J. Spectr. Theory, 9 (2019), 1063–1087.

    Article  MathSciNet  Google Scholar 

  13. C. Fefferman and M. Weinstein, Honeycomb lattice potentials and Dirac points, J. Amer. Math. Soc. 25 (2012), 1169–1220.

    Article  MathSciNet  Google Scholar 

  14. C. Fefferman and M. Weinstein, Edge States of continuum Schroedinger operators for sharply terminated honeycomb structures, arXiv:1810.03497.

  15. C. Fefferman, J. P. Lee-Thorp and M. Weinstein, Honeycomb Schroedinger operators in the strong binding regime, Commun. Pure Appl. Math. 71 (2018), 1178–1270.

    Article  Google Scholar 

  16. J. Fillman and R. Han, preprint in preparation.

  17. D. Gieseker, H. Knörrer and E. Trubowitz, The Geometry of Algebraic Fermi Curves, Academic Press, Boston, MA, 1993.

    MATH  Google Scholar 

  18. R. Han, Absence of point spectrum for the self-dual extended Harper’s model, Int. Math. Res. Not. IMRN 9 (2018), 2801–2809.

    MathSciNet  MATH  Google Scholar 

  19. R. Han, Dry Ten Martini problem for the non-self-dual extended Harper’s model, Trans. Amer. Math. Soc. 370 (2018), 197–217.

    Article  MathSciNet  Google Scholar 

  20. R. Han, S. Jitomirskaya, Full measure reducibility and localization for quasiperiodic Jacobi operators: A topological criterion, Adv. Math. 319 (2017), 224–250.

    Article  MathSciNet  Google Scholar 

  21. R. Han and S. Jitomirskaya, Discrete Bethe-Sommerfeld Conjecture, Commun. Math. Phys. 361 (2018), 205–216.

    Article  MathSciNet  Google Scholar 

  22. J. H. Han, D. J. Thouless, H. Hiramoto and M. Kohmoto, Critical and bicritical properties of Harper’s equation with next-nearest-neighbor coupling, Phys. Rev. B 50 (1994), 11365.

    Article  Google Scholar 

  23. B. Helffer, P. Kerdelhué and J. Royo-Letelier, Chambers’s formula for the graphene and the Hou model with kagome periodicity and applications, Ann. Henri Poincaré 17 (2016), 795–818.

    Article  MathSciNet  Google Scholar 

  24. B. Helffer and A. Mohamed, Asymptotics of the density of states for the Schrödinger operator with periodic electric potential, Duke Math. J. 92 (1998), 1–60.

    Article  MathSciNet  Google Scholar 

  25. S. Jitomirskaya and C. A. Marx, Analytic quasi-perodic cocycles with singularities and the Lyapunov exponent of extended Harper’s model, Comm. Math. Phys. 316 (2012), 237–267.

    Article  MathSciNet  Google Scholar 

  26. Y. E. Karpeshina, Perturbation Theory for the Schrödinger Operator with a Periodic Potential, Springer, Berlin, 1997.

    Book  Google Scholar 

  27. E. Korotyaev and N. Saburova, Schrödinger operators on periodic discrete graphs, J. Math. Anal. Appl. 420 (2014), 576–611.

    Article  MathSciNet  Google Scholar 

  28. H. Krüger, Periodic and limit-periodic discrete Schrödinger operators, preprint, arXiv:1108.1584

  29. P. Kuchment, O. Post, On the spectra of carbon nano-structures, Comm. Math. Phys. 275 (2007), 805–882.

    Article  MathSciNet  Google Scholar 

  30. P. Van Mouche, The coexistence problem for the discrete Mathieu operator, Comm. Math. Phys. 122 (1989), 23–33.

    Article  MathSciNet  Google Scholar 

  31. K. Novoselov, Nobel lecture: Graphene: Materials in the flatland, Rev. Modern Phys. 83 (2011), 837–849.

    Article  Google Scholar 

  32. L. Parnovski, Bethe-Sommerfeld conjecture, Ann. Henri Poincaré 9 (2008), 457–508.

    Article  MathSciNet  Google Scholar 

  33. L. Parnovski and A. V. Sobolev, On the Bethe-Sommerfeld conjecture for the polyharmonic operator, Duke Math. J. 107 (2001), 209–238.

    Article  MathSciNet  Google Scholar 

  34. L. Parnovski and A. V. Sobolev, Perturbation theory and the Bethe-Sommerfeld conjecture, Ann. Henri Poincaré 2 (2001), 573–581.

    Article  MathSciNet  Google Scholar 

  35. V. N. Popov and M. Skriganov, A remark on the spectral structure of the two dimensional Schrödinger operator with a periodic potential, Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov. (LOMI) 109 (1981), 131–133.

    MathSciNet  MATH  Google Scholar 

  36. O. Post, Spectral Analysis on Graph-Like Spaces, Springer, Heidelberg, 2012.

    Book  Google Scholar 

  37. M. Skriganov, Proof of the Bethe-Sommerfeld conjecture in dimension two, Soviet Math. Dokl. 20 (1979), 89–90.

    MATH  Google Scholar 

  38. M. Skriganov, Geometric and arithmetic methods in the spectral theory of multidimensional periodic operators, Proc. Steklov Math. Inst. 171 (1984), 3–122.

    Google Scholar 

  39. M. Skriganov, The spectrum band structure of the three-dimensional Schrödinger operator with periodic potential, Inv. Math. 80 (1985), 107–121.

    Article  Google Scholar 

  40. D. J. Thouless, Bandwidth for a quasiperiodic tight binding model, Phys. Rev. B 28 (1983), 4272–4276.

    Article  Google Scholar 

  41. O. A. Veliev, Spectrum of multidimensional periodic operators, Teor. Funktsiĭ Funktsional. Anal. i Prilozhen 49 (1988), 17–34.

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

We would like to thank Svetlana Jitomirskaya for comments on an earlier version of the manuscript, and Tom Spencer for useful discussions. R. H. would like to thank IAS, Princeton, for its hospitality during the 2017–18 academic year, and Virginia Tech for its hospitality during which part of the work was done. R. H. is supported in part by the National Science Foundation under Grant No. DMS-1638352 and DMS-1800689. J. F. was supported in part by an AMS Simons Travel Grant 2016–2018 and Simons Collaboration Grant #711663.

Author information

Authors and Affiliations

  1. Department of Mathematics, MCS 470, Texas State University, 601 University Dr., San Marcos, TX, 78666, USA

    Jake Fillman

  2. Department of Mathematics, Louisiana State University, Lockett Hall, Baton Rouge, LA, 70802, USA

    Rui Han

Authors
  1. Jake Fillman
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Rui Han
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Jake Fillman or Rui Han.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fillman, J., Han, R. Discrete Bethe-Sommerfeld conjecture for triangular, square, and hexagonal lattices. JAMA 142, 271–321 (2020). https://doi.org/10.1007/s11854-020-0138-z

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11854-020-0138-z

Search

Navigation