Skip to main content
SpringerLink
Log in

A Critical Review on Inertially-Amplified Passive Vibration Control Devices

  • Review article
  • Published:
Archives of Computational Methods in Engineering Aims and scope Submit manuscript

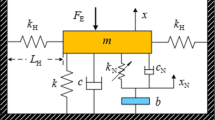
Abstract

Resonators, inertial amplifiers, negative stiffness devices, and impacting oscillators are added to the core materials of conventional passive vibration isolation systems to address their shortcomings. In order to manage the vibration of dynamic systems with a single or multiple degrees of freedom, unique linear and nonlinear passive vibration isolation systems are introduced in this study. In order to construct the governing equations of motion for the controlled dynamic systems, Newton’s second law and Lagrange’s equation are both utilised. The statistical linearization approach is used to linearize each nonlinear component of the governing equations of motion of the controlled structures. To get the precise closed-form equations for the ideal design parameters of each innovative passive vibration isolation system, \(H_2\) and \(H_\infty\) optimisation methods are used. By using these ideal design criteria, the best innovative passive vibration isolation systems with reliable vibration reduction capability have been produced. The transfer function generation and harmonic balance methods are used to determine the dynamic responses of the controlled structures subjected to harmonic, random-white noise excitations analytically. These dynamic responses are used to determine each unique vibration control device’s frequency domain dynamic response reduction capabilities. A numerical analysis is also conducted to further establish the dynamic reaction capabilities, such as displacement and acceleration reduction capacities in the time domain while taking the Newmark-Beta approach into consideration. The near-field (i.e., pulse and without pulse records) earthquake records are used as the basis excitations in this numerical analysis. Overall, a critical review of passive vibration control devices is presented in this paper to demonstrate their recent advances.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

Data Availability

All data, models, and code generated or used during the study appear in the submitted article.

References

  1. Kelly JM (1990) Base isolation: linear theory and design. Earthq Spectra 6(2):223–244

    Google Scholar 

  2. Makris N (2019) Seismic isolation: early history. Earthq Eng Struct Dyn 48(2):269–283

    Google Scholar 

  3. Touaillon J (1870) Improvement in buildings, U.S. Patent No. 99973

  4. Wei X, Lui H, Qin Y (2011) Fault isolation of rail vehicle suspension systems by using similarity measure. In: Proceedings of 2011 IEEE international conference on service operations, logistics and informatics. IEEE, pp 391–396

  5. Esmailzadeh E (1978) Optimization of pneumatic vibration isolation system for vehicle suspension

  6. Aly AA, Salem FA (2013) Vehicle suspension systems control: a review. Int J Control Autom Syst 2(2):46–54

    Google Scholar 

  7. Du H, Li W, Zhang N (2011) Semi-active variable stiffness vibration control of vehicle seat suspension using an MR elastomer isolator. Smart Mater Struct 20(10):105003

    Google Scholar 

  8. Ebrahimi B, Bolandhemmat H, Khamesee MB, Golnaraghi F (2011) A hybrid electromagnetic shock absorber for active vehicle suspension systems. Veh Syst Dyn 49(1–2):311–332

    Google Scholar 

  9. Lindberg E, Östberg M, Hörlin N-E, Göransson P (2014) A vibro-acoustic reduced order model using undeformed coupling interface substructuring-application to rubber bushing isolation in vehicle suspension systems. Appl Acoust 78:43–50

    Google Scholar 

  10. Malhotra PK (1997) New method for seismic isolation of liquid-storage tanks. Earthq Eng Struct Dyn 26(8):839–847

    Google Scholar 

  11. Das A, Deb SK, Dutta A (2016) Shake table testing of un-reinforced brick masonry building test model isolated by u-frei. Earthq Eng Struct Dyn 45(2):253–272

    Google Scholar 

  12. Cheng X, Jing W, Gong L (2017) Simplified model and energy dissipation characteristics of a rectangular liquid-storage structure controlled with sliding base isolation and displacement-limiting devices. J Perform Constr Facil 31(5):04017071

    Google Scholar 

  13. Schnitzer E (1956) Band-pass Shock and Vibration Absorbers for Application to Aircraft Landing Gear, no. 3803, National Advisory Committee for Aeronautics

  14. Jadhav M, Jangid R (2004) Response of base-isolated liquid storage tanks. Shock Vib 11(1):33–45

    Google Scholar 

  15. Panchal V, Jangid R (2011) Seismic response of liquid storage steel tanks with variable frequency pendulum isolator. KSCE J Civ Eng 15:1041–1055

    Google Scholar 

  16. Tsai C, Chiang T-C, Chen B-J (2003) Finite element formulations and theoretical study for variable curvature friction pendulum system. Eng Struct 25(14):1719–1730

    Google Scholar 

  17. Murnal P, Sinha R (2002) Earthquake resistant design of structures using the variable frequency pendulum isolator. J Struct Eng 128(7):870–880

    Google Scholar 

  18. Shrimali M, Jangid R (2004) Seismic analysis of base-isolated liquid storage tanks. J Sound Vib 275(1–2):59–75

    Google Scholar 

  19. Panchal V, Jangid R (2012) Behaviour of liquid storage tanks with VCFPS under near-fault ground motions. Struct Infrastruct Eng 8(1):71–88

    Google Scholar 

  20. Liang B, Tang J-X (1994) Vibration studies of base-isolated liquid storage tanks. Comput Struct 52(5):1051–1059

    Google Scholar 

  21. Abalı E, Uckan E (2010) Parametric analysis of liquid storage tanks base isolated by curved surface sliding bearings. Soil Dyn Earthq Eng 30(1–2):21–31

    Google Scholar 

  22. Frahm H (1909) Devices for damping vibration of bodies, US Patent (989958)

  23. Bai X-X, Jiang P, Qian L-J (2017) Integrated semi-active seat suspension for both longitudinal and vertical vibration isolation. J Intell Mater Syst Struct 28(8):1036–1049

    Google Scholar 

  24. Marano GC, Greco R, Chiaia B (2010) A comparison between different optimization criteria for tuned mass dampers design. J Sound Vib 329(23):4880–4890

    Google Scholar 

  25. Kaynia AM, Veneziano D, Biggs JM (1981) Seismic effectiveness of tuned mass dampers. J Struct Div 107(8):1465–1484

    Google Scholar 

  26. Kopylov S, Chen Z, Abdelkareem MA (2020) Implementation of an electromagnetic regenerative tuned mass damper in a vehicle suspension system. IEEE Access 8:110153–110163

    Google Scholar 

  27. Jing W, Feng J, Cheng X, Yang W (2023) Seismic response reduction of liquid storage tank using a passive system based on improved tuned mass damper. Int J Struct Stab Dyn 2450089

  28. McNamara RJ (1977) Tuned mass dampers for buildings. J Struct Div 103(9):1785–1798

    Google Scholar 

  29. Caicedo D, Lara-Valencia L, Blandon J, Graciano C (2021) Seismic response of high-rise buildings through metaheuristic-based optimization using tuned mass dampers and tuned mass dampers inerter. J Build Eng 34:101927

    Google Scholar 

  30. Araz O, Kahya V (2022) Optimization of multiple tuned mass dampers for a two-span continuous railway bridge via differential evolution algorithm. In: Structures, vol 39. Elsevier, Amsterdam, pp 29–38

  31. Pisal AY, Jangid R (2016) Dynamic response of structure with tuned mass friction damper. Int J Adv Struct Eng 8:363–377

    Google Scholar 

  32. Gewei Z, Basu B (2011) A study on friction-tuned mass damper: harmonic solution and statistical linearization. J Vib Control 17(5):721–731

    MathSciNet  Google Scholar 

  33. Pisal AY, Jangid R (2016) Vibration control of bridge subjected to multi-axle vehicle using multiple tuned mass friction dampers. Int J Adv Struct Eng 8:213–227

    Google Scholar 

  34. Kazeminezhad E, Kazemi MT, Mirhosseini SM (2020) Assessment of the vertical stiffness of elastomeric bearing due to displacement and rotation. Int J Non-Linear Mech 119:103306

    Google Scholar 

  35. Wang J, Lin C, Chen B (2003) Vibration suppression for high-speed railway bridges using tuned mass dampers. Int J Solids Struct 40(2):465–491

    Google Scholar 

  36. Hwang J, Chiou J (1996) An equivalent linear model of lead-rubber seismic isolation bearings. Eng Struct 18(7):528–536

    Google Scholar 

  37. Dai J, Xu Z-D, Gai P-P, Hu Z-W (2021) Optimal design of tuned mass damper inerter with a maxwell element for mitigating the vortex-induced vibration in bridges. Mech Syst Signal Process 148:107180

    Google Scholar 

  38. Dai J, Xu Z-D, Gai P-P (2020) Parameter determination of the tuned mass damper mitigating the vortex-induced vibration in bridges. Eng Struct 221:111084

    Google Scholar 

  39. Adhikari S, Woodhouse J (2001) Identification of damping: part 2, non-viscous damping. J Sound Vib 243(1):63–88

    Google Scholar 

  40. Rosenblueth E, Herrera I (1964) On a kind of hysteretic damping. J Eng Mech Div 90(4):37–48

    Google Scholar 

  41. Buckle IG (1985) New Zealand seismic base isolation concepts and their application to nuclear engineering. Nucl Eng Des 84(3):313–326

    Google Scholar 

  42. Robinson WH (1982) Lead-rubber hysteretic bearings suitable for protecting structures during earthquakes. Earthq Eng Struct Dyn 10(4):593–604

    Google Scholar 

  43. Jangid R (2005) Computational numerical models for seismic response of structures isolated by sliding systems. Struct Control Health Monit 12(1):117–137

    Google Scholar 

  44. Jangid R (2005) Optimum friction pendulum system for near-fault motions. Eng Struct 27(3):349–359

    Google Scholar 

  45. Shakib H, Fuladgar A (2003) Response of pure-friction sliding structures to three components of earthquake excitation. Comput Struct 81(4):189–196

    Google Scholar 

  46. Billah AM, Todorov B (2019) Effects of subfreezing temperature on the seismic response of lead rubber bearing isolated bridge. Soil Dyn Earthq Eng 126:105814

    Google Scholar 

  47. Chen X, Ikago K, Guan Z, Li J, Wang X (2022) Lead-rubber-bearing with negative stiffness springs (lrb-ns) for base-isolation seismic design of resilient bridges: a theoretical feasibility study. Eng Struct 266:114601

    Google Scholar 

  48. Ebrahimi H, Kianfar K, Bijari M (2021) Scheduling a cellular manufacturing system based on price elasticity of demand and time-dependent energy prices. Comput Ind Eng 159:107460

    Google Scholar 

  49. Jangid R (2008) Equivalent linear stochastic seismic response of isolated bridges. J Sound Vib 309(3–5):805–822

    Google Scholar 

  50. Soneji B, Jangid R (2006) Effectiveness of seismic isolation for cable-stayed bridges. Int J Struct Stab Dyn 6(01):77–96

    Google Scholar 

  51. Raei M, Dardel M (2020) Tuned mass damper and high static low dynamic stiffness isolator for vibration reduction of beam structure. Proc Inst Mech Eng Part K 234(1):95–115

    Google Scholar 

  52. De Domenico D, Ricciardi G, Zhang R (2020) Optimal design and seismic performance of tuned fluid inerter applied to structures with friction pendulum isolators. Soil Dyn Earthq Eng 132:106099

    Google Scholar 

  53. Bouna HS, Nbendjo BN, Woafo P (2020) Isolation performance of a quasi-zero stiffness isolator in vibration isolation of a multi-span continuous beam bridge under pier base vibrating excitation. Nonlinear Dyn 100:1125–1141

    Google Scholar 

  54. Elettore E, Freddi F, Latour M, Rizzano G (2021) Design and analysis of a seismic resilient steel moment resisting frame equipped with damage-free self-centering column bases. J Constr Steel Res 179:106543

    Google Scholar 

  55. Mazza F (2019) Effects of the long-term behaviour of isolation devices on the seismic response of base-isolated buildings. Struct Control Health Monit 26(4):e2331

    Google Scholar 

  56. Fang H, Liu L, Zhang D, Wen M (2019) Tuned mass damper on a damped structure. Struct Control Health Monit 26(3):e2324

    Google Scholar 

  57. Li H-W, Xu Z-D, Wang F, Gai P-P, Gomez D, Dyke SJ (2023) Development and validation of a nonlinear model to describe the tension-compression behavior of rubber-like base isolators. J Eng Mech 149(2):04022104

    Google Scholar 

  58. Rahgozar A, Estekanchi HE, Mirfarhadi SA (2023) On optimal lead rubber base-isolation design for steel moment frames using value-based seismic design approach. Soil Dyn Earthq Eng 164:107520

    Google Scholar 

  59. Gudainiyan J, Gupta PK (2023) A comparative study on the response of the l-shaped base isolated multi-storey building to near and far field earthquake ground motion. Forces Mech 11:100191

    Google Scholar 

  60. Forcellini D, Kalfas KN (2023) Inter-story seismic isolation for high-rise buildings. Eng Struct 275:115175

    Google Scholar 

  61. Movahhed AS, Shirkhani A, Zardari S, Mashayekhi M, Farsangi EN, Majdi A (2023) Modified endurance time method for seismic performance assessment of base-isolated structures. J Build Eng 67:105955

    Google Scholar 

  62. Chowdhury S, Banerjee A, Adhikari S (2023) Nonlinear inertial amplifier resilient friction base isolators for multiple degrees of freedom systems. Mech Adv Mater Struct 1–8

  63. Gao H, Xing C, Wang H, Li J, Zhang Y (2023) Performance improvement and demand-oriented optimum design of the tuned negative stiffness inerter damper for base-isolated structures. J Build Eng 63:105488

    Google Scholar 

  64. Chowdhury S, Banerjee A, Adhikari S (2023) The optimal design of negative stiffness inerter passive dampers for structures. Int J Mech Sci 108551

  65. Chowdhury S, Banerjee A, Adhikari S (2023) The optimum inertial amplifier viscoelastic base isolators for dynamic response mitigation of structures: an analytical study. J Struct Integrity Maintenance 1–11

  66. Zhang C, Duan C, Sun L, Zhu L, Hsiao P-C (2023) Shaking table test of multiple-type isolation control strategies for high-rise structure based on friction pendulum. Soil Dyn Earthq Eng 171:107935

    Google Scholar 

  67. Ershadbakhsh AM, Ghorbani-Tanha AK, Fallahi R (2023) A novel active tendon pendulum tuned mass damper and its application in transient vibration control. In: Structures, vol 47. Elsevier, Amsterdam, pp 2273–2280

  68. Fahimi Farzam M, Charkhtab Basim M, Maroofiazar R (2023) Efficiency and robustness of optimally designed tuned mass dampers for mid-and high-rise buildings under far and near-field earthquakes. J Vib Eng Technol 11(2):699–719

    Google Scholar 

  69. Patro SR, Banerjee A, Adhikari S, Ramana G (2022) Kaimal spectrum based h2 optimization of tuned mass dampers for wind turbines. J Vib Control 10775463221092838

  70. Sinha A (2009) Optimal damped vibration absorber for narrow band random excitations: a mixed \(h_2\)/\(h_\infty\) optimization. Probab Eng Mech 24(2):251–254

    Google Scholar 

  71. Asami T, Nishihara O, Baz AM (2002) Analytical solutions to \(h_{\infty }\) and \(h_2\) optimization of dynamic vibration absorbers attached to damped linear systems. J Vib Acoust 124(2):284–295

    Google Scholar 

  72. Asami T, Nishihara O (2002) \(h_2\) optimization of the three-element type dynamic vibration absorbers. J Vib Acoust 124(4):583–592

    Google Scholar 

  73. Cheung Y, Wong WO (2011) \(h_2\) optimization of a non-traditional dynamic vibration absorber for vibration control of structures under random force excitation. J Sound Vib 330(6):1039–1044

    Google Scholar 

  74. Palmeri A, Lombardo M (2011) A new modal correction method for linear structures subjected to deterministic and random loadings. Comput Struct 89(11–12):844–854

    Google Scholar 

  75. Khodaparast HH, Mottershead JE, Friswell MI (2008) Perturbation methods for the estimation of parameter variability in stochastic model updating. Mech Syst Signal Process 22(8):1751–1773

    Google Scholar 

  76. Khodaparast HH, Mottershead J (2008) Efficient methods in stochastic model updating. Stoch Model 7(8):9

    Google Scholar 

  77. Adhikari S, Friswell M, Litak G, Khodaparast HH (2016) Design and analysis of vibration energy harvesters based on peak response statistics. Smart Mater Struct 25(6):065009

    Google Scholar 

  78. Dey S, Mukhopadhyay T, Khodaparast HH, Adhikari S (2016) A response surface modelling approach for resonance driven reliability based optimization of composite shells. Periodica Polytechnica Civ Eng 60(1):103–111

    Google Scholar 

  79. Den Hartog JP (1985) Mechanical vibrations. Courier Corporation, North Chelmsford

    Google Scholar 

  80. Cheung Y, Wong WO (2011) \(h_{\infty }\) optimization of a variant design of the dynamic vibration absorber-revisited and new results. J Sound Vib 330(16):3901–3912

    Google Scholar 

  81. Allen JC (2012) \(H_{\infty }\) engineering and amplifier optimization. Springer, New York

    Google Scholar 

  82. Mukhopadhyay T, Adhikari S (2017) Stochastic mechanics of metamaterials. Compos Struct 162:85–97

    Google Scholar 

  83. Hua Y, Wong W, Cheng L (2018) Optimal design of a beam-based dynamic vibration absorber using fixed-points theory. J Sound Vib 421:111–131

    Google Scholar 

  84. Chun S, Lee Y, Kim T-H (2015) \(h_{\infty }\) optimization of dynamic vibration absorber variant for vibration control of damped linear systems. J Sound Vib 335:55–65

    Google Scholar 

  85. Islam NU, Jangid R (2023) Optimum parameters and performance of negative stiffness and inerter based dampers for base-isolated structures. Bull Earthq Eng 21(3):1411–1438

    Google Scholar 

  86. Xiao L, Bursi OS, Li H, Wang M, Du X-L (2023) Energy dissipation enhancement of flexural metamaterial beams with inerter and rotational deformation. Int J Mech Sci 237:107770

    Google Scholar 

  87. Smith MC (2002) Synthesis of mechanical networks: the inerter. IEEE Trans Autom Control 47(10):1648–1662

    MathSciNet  Google Scholar 

  88. Li H, Yao H, Cao Y, Jia R, Dou J (2023) Chiral metamaterial-inerter nonlinear energy sink for torsional vibration suppression of the rotor system. Mech Syst Signal Process 200:110640

    Google Scholar 

  89. Kalderon M, Mantakas A, Antoniadis I (2023) Dynamic modelling and experimental testing of a dynamic directional amplification mechanism for vibration mitigation. J Vib Eng Technol 1–12

  90. Li Y, Tan P, Li S, He H (2023) A novel tuned inerter eddy current damper: modeling, optimization, and evaluation. Eng Struct 285:116026

    Google Scholar 

  91. Chen Q, Zhang L, Zhang R, Pan C et al (2023) Seismic performance of an underground structure with an inerter-based isolation system. Struct Control Health Monit

  92. Li Z, Ma R, Xu K, Han Q (2024) Closed-form solutions for the optimal design of lever-arm tuned mass damper inerter (ltmdi). Mech Syst Signal Process 206:110889

    Google Scholar 

  93. Chen MZ, Hu Y (2019) Inerter and its application in vibration control systems. Springer, New York

    Google Scholar 

  94. Carrella A, Brennan M, Waters T (2007) Static analysis of a passive vibration isolator with quasi-zero-stiffness characteristic. J Sound Vib 301(3–5):678–689

    Google Scholar 

  95. Cheng C, Li S, Wang Y, Jiang X (2016) On the analysis of a high-static-low-dynamic stiffness vibration isolator with time-delayed cubic displacement feedback. J Sound Vib 378:76–91

    Google Scholar 

  96. Huang X, Liu X, Sun J, Zhang Z, Hua H (2014) Vibration isolation characteristics of a nonlinear isolator using Euler buckled beam as negative stiffness corrector: a theoretical and experimental study. J Sound Vib 333(4):1132–1148

    Google Scholar 

  97. Iemura H, Pradono MH (2009) Advances in the development of pseudo-negative-stiffness dampers for seismic response control. Struct Control Health Monit 16(7–8):784–799

    Google Scholar 

  98. Lakes RS, Lee T, Bersie A, Wang Y-C (2001) Extreme damping in composite materials with negative-stiffness inclusions. Nature 410(6828):565–567

    Google Scholar 

  99. Shi X, Zhu S (2017) Simulation and optimization of magnetic negative stiffness dampers. Sens Actuators A 259:14–33

    Google Scholar 

  100. Acar G, Yilmaz C (2013) Experimental and numerical evidence for the existence of wide and deep phononic gaps induced by inertial amplification in two-dimensional solid structures. J Sound Vib 332(24):6389–6404

    Google Scholar 

  101. Yilmaz C, Hulbert GM (2017) Dynamics of locally resonant and inertially amplified lattice materials. In: Phani AS, Hussein MI (eds) Dynamics of lattice materials, p 233

  102. Frandsen NM, Bilal OR, Jensen JS, Hussein MI (2016) Inertial amplification of continuous structures: large band gaps from small masses. J Appl Phys 119(12):124902

    Google Scholar 

  103. Chowdhury S, Banerjee A (2023) The optimum enhanced base isolators applied to MDOF systems: exact closed-form expressions. J Vib Eng Technol

  104. Huang H, Sun C, Huang G (2009) On the negative effective mass density in acoustic metamaterials. Int J Eng Sci 47(4):610–617

    Google Scholar 

  105. Kulkarni PP, Manimala JM (2016) Longitudinal elastic wave propagation characteristics of inertant acoustic metamaterials. J Appl Phys 119(24)

  106. DePauw D, Singh T, Nouh M et al (2018) Dispersion transitions and pole-zero characteristics of finite inertially amplified acoustic metamaterials. J Appl Phys 123(10)

  107. Taniker S, Yilmaz C (2017) Generating ultra wide vibration stop bands by a novel inertial amplification mechanism topology with flexure hinges. Int J Solids Struct 106:129–138

    Google Scholar 

  108. Li J, Li S (2018) Generating ultra wide low-frequency gap for transverse wave isolation via inertial amplification effects. Phys Lett A 382(5):241–247

    MathSciNet  Google Scholar 

  109. Li Y, Li X, Ding J (2023) Broadband low-frequency flexural wave attenuation in beam-type metastructures with double-sides inertial amplified resonators. J Vib Control 29(21–22):4924–4934

    MathSciNet  Google Scholar 

  110. Orta AH, Yilmaz C (2019) Inertial amplification induced phononic band gaps generated by a compliant axial to rotary motion conversion mechanism. J Sound Vib 439:329–343

    Google Scholar 

  111. Yuksel O, Yilmaz C (2020) Realization of an ultrawide stop band in a 2-d elastic metamaterial with topologically optimized inertial amplification mechanisms. Int J Solids Struct 203:138–150

    Google Scholar 

  112. Taniker S, Yilmaz C (2015) Design, analysis and experimental investigation of three-dimensional structures with inertial amplification induced vibration stop bands. Int J Solids Struct 72:88–97

    Google Scholar 

  113. Zhang W, Zhang W, Guo X (2023) Vertical vibration control using nonlinear energy sink with inertial amplifier. Appl Math Mech 44(10):1721–1738

    MathSciNet  Google Scholar 

  114. Hellegouarch S, Fueyo Roza L, Artoos K, Lambert P, Collette C (2016) Linear encoder based low frequency inertial sensor. Int J Optomechatronics 10(3–4):120–129

    Google Scholar 

  115. Zhao C, Zhang K, Zhao P, Deng Z (2023) Finite-amplitude nonlinear waves in inertial amplification metamaterials: theoretical and numerical analyses. J Sound Vib 560:117802

    Google Scholar 

  116. Zhao C, Zhang K, Zhao P, Hong F, Deng Z (2023) Bandgap merging and backward wave propagation in inertial amplification metamaterials. Int J Mech Sci 250:108319

    Google Scholar 

  117. Settimi V, Lepidi M, Bacigalupo A (2023) Analytical spectral design of mechanical metamaterials with inertia amplification. Eng Struct 274:115054

    Google Scholar 

  118. Gao H, Zhu J, Qu Y, Meng G (2023) Inertia modulated meta-structure with time-varying inertia amplification. J Appl Mech 1–21

  119. Čeponis A, Jūrėnas V, Mažeika D, Bakanauskas V, Deltuvienė D (2023) Rod-shaped linear inertial type piezoelectric actuator. In: Actuators, vol 12, MDPI, p 379

  120. Mori H, Sueda M, Shiroshita K, Kondou T (2023) Effect of damping and rotor moment of inertia on stability of self-synchronization for two unbalanced rotors. J Sound Vib 570:118103

    Google Scholar 

  121. Mao Q, Yuan W, Wu J (2023) Design and experimental study of a multiple-degree-of-freedom vibration absorber by using an inertial actuator. Int J Struct Stab Dyn 2450006

  122. Pan T, Shen X, Chen Y (2023) Active vibration control of thin-walled structure with inertial piezoelectric actuator based on fuzzy adaptive pid algorithm. J Vib Eng Technol 1–16

  123. Banerjee A, Adhikari S, Hussein MI (2021) Inertial amplification band-gap generation by coupling a levered mass with a locally resonant mass. Int J Mech Sci 207:106630

    Google Scholar 

  124. Oliveto ND, Markou AA, Athanasiou A (2019) Modeling of high damping rubber bearings under bidirectional shear loading. Soil Dyn Earthq Eng 118:179–190

    Google Scholar 

  125. Zhou F, Zhang Z, Wu D, Zhu H (2018) An analytical model for predicting the lateral-torsion coupling property of laminated rubber bearings. J Sound Vib 427:1–14

    Google Scholar 

  126. Kim JH, Kim MK, Choi I-K (2019) Experimental study on seismic behavior of lead-rubber bearing considering bi-directional horizontal input motions. Eng Struct 198:109529

    Google Scholar 

  127. Wei B, Zuo C, He X, Jiang L (2018) Numerical investigation on scaling a pure friction isolation system for civil structures in shaking table model tests. Int J Non-Linear Mech 98:1–12

    Google Scholar 

  128. Hong W-K, Kim H-C (2004) Performance of a multi-story structure with a resilient-friction base isolation system. Comput Struct 82(27):2271–2283

    Google Scholar 

  129. Kelly JM (1986) Aseismic base isolation: review and bibliography. Soil Dyn Earthq Eng 5(4):202–216

    Google Scholar 

  130. De Luca A, Guidi LG (2019) State of art in the worldwide evolution of base isolation design. Soil Dyn Earthq Eng 125:105722

    Google Scholar 

  131. Fan H, Yang L, Tian Y, Wang Z (2020) Design of metastructures with quasi-zero dynamic stiffness for vibration isolation. Compos Struct 243:112244

    Google Scholar 

  132. Zhang C, Ali A (2021) The advancement of seismic isolation and energy dissipation mechanisms based on friction. Soil Dyn Earthq Eng 146:106746

    Google Scholar 

  133. Xu Y, Becker TC, Guo T (2021) Design optimization of triple friction pendulums for high-rise buildings considering both seismic and wind loads. Soil Dyn Earthq Eng 142:106568

    Google Scholar 

  134. Hui Y, Law S-S, Zhu W, Wang Q (2021) Internal resonance of structure with hysteretic base-isolation and its application for seismic mitigation. Eng Struct 229:111643

    Google Scholar 

  135. Eliseev S (1978) Structural theory of vibration protection systems

  136. Rivin EI (2003) Passive vibration isolation

  137. Smith MC (2020) The inerter: a retrospective. Annu Rev Control Robot Autonomous Syst 3:361–391

    Google Scholar 

  138. Smith MC, Wang F-C (2004) Performance benefits in passive vehicle suspensions employing inerters. Veh Syst Dyn 42(4):235–257

    Google Scholar 

  139. Wang F-C, Liao M-K, Liao B-H, Su W-J, Chan H-A (2009) The performance improvements of train suspension systems with mechanical networks employing inerters. Veh Syst Dyn 47(7):805–830

    Google Scholar 

  140. Wang F-C, Yu C-H, Chang M-L, Hsu M (2006) The performance improvements of train suspension systems with inerters. In: Proceedings of the 45th IEEE conference on decision and control. IEEE, pp 1472–1477

  141. Wang F-C, Hsieh M-R, Chen H-J (2012) Stability and performance analysis of a full-train system with inerters. Veh Syst Dyn 50(4):545–571

    Google Scholar 

  142. Hu Y, Chen MZ, Sun Y (2017) Comfort-oriented vehicle suspension design with skyhook inerter configuration. J Sound Vib 405:34–47

    Google Scholar 

  143. Kuhnert WM, Gonçalves PJP, Ledezma-Ramirez DF, Brennan MJ (2020) Inerter-like devices used for vibration isolation: a historical perspective. J Franklin Inst

  144. Qian F, Luo Sr Y, Sun H, Tai WC, Zuo L (2019) Performance enhancement of a base-isolation structure using optimal tuned inerter dampers. In: Active and passive smart structures and integrated systems XIII, vol 10967. International Society for Optics and Photonics, p 1096715

  145. Sun H, Zuo L, Wang X, Peng J, Wang W (2019) Exact h2 optimal solutions to inerter-based isolation systems for building structures. Struct Control Health Monit 26(6):e2357

    Google Scholar 

  146. Zhao Z, Chen Q, Zhang R, Pan C, Jiang Y (2020) Energy dissipation mechanism of inerter systems. Int J Mech Sci 184:105845

    Google Scholar 

  147. Moghimi G, Makris N (2020) Seismic response of yielding structures equipped with inerters. Soil Dyn Earthq Eng 141:106474

    Google Scholar 

  148. Li L, Liang Q (2019) Effect of inerter for seismic mitigation comparing with base isolation. Struct Control Health Monit 26(10):e2409

    Google Scholar 

  149. Jiang Y, Zhao Z, Zhang R, De Domenico D, Pan C (2020) Optimal design based on analytical solution for storage tank with inerter isolation system. Soil Dyn Earthq Eng 129:105924

    Google Scholar 

  150. Zhao Z, Zhang R, Wierschem NE, Jiang Y, Pan C (2020) Displacement mitigation–oriented design and mechanism for inerter-based isolation system. J Vib Control 1077546320951662

  151. Chowdhury S, Banerjee A (2023) The optimum enhanced base isolators applied to mdof systems: Exact closed-form expressions. J Vib Eng Technol 1–18

  152. Zhao Z, Zhang R, Jiang Y, Pan C (2019) Seismic response mitigation of structures with a friction pendulum inerter system. Eng Struct 193:110–120

    Google Scholar 

  153. Zhao Z, Chen Q, Zhang R, Pan C, Jiang Y (2019) Optimal design of an inerter isolation system considering the soil condition. Eng Struct 196:109324

    Google Scholar 

  154. Zhang R, Zhao Z, Pan C (2018) Influence of mechanical layout of inerter systems on seismic mitigation of storage tanks. Soil Dyn Earthq Eng 114:639–649

    Google Scholar 

  155. Zhang R, Zhao Z, Dai K (2019) Seismic response mitigation of a wind turbine tower using a tuned parallel inerter mass system. Eng Struct 180:29–39

    Google Scholar 

  156. Panchal V, Jangid R (2009) Seismic response of structures with variable friction pendulum system. J Earthq Eng 13(2):193–216

    Google Scholar 

  157. Soni D, Mistry B, Jangid R, Panchal V (2011) Seismic response of the double variable frequency pendulum isolator. Struct Control Health Monit 18(4):450–470

    Google Scholar 

  158. Taflanidis AA, Giaralis A, Patsialis D (2019) Multi-objective optimal design of inerter-based vibration absorbers for earthquake protection of multi-storey building structures. J Franklin Inst 356(14):7754–7784

    Google Scholar 

  159. Čakmak D, Tomičević Z, Wolf H, Božić Ž, Semenski D, Trapić I (2019) Vibration fatigue study of the helical spring in the base-excited inerter-based isolation system. Eng Fail Anal 103:44–56

    Google Scholar 

  160. Chen MZ, Hu Y (2019) Analysis for inerter-based vibration system. In: Inerter and its application in vibration control systems. Springer, New York, pp 19–39

  161. Yilmaz C, Hulbert GM, Kikuchi N (2007) Phononic band gaps induced by inertial amplification in periodic media. Phys Rev B 76(5):054309

    Google Scholar 

  162. Yuksel O, Yilmaz C (2015) Shape optimization of phononic band gap structures incorporating inertial amplification mechanisms. J Sound Vib 355:232–245

    Google Scholar 

  163. Yilmaz C, Hulbert G (2010) Theory of phononic gaps induced by inertial amplification in finite structures. Phys Lett A 374(34):3576–3584

    Google Scholar 

  164. Zhou J, Dou L, Wang K, Xu D, Ouyang H (2019) A nonlinear resonator with inertial amplification for very low-frequency flexural wave attenuations in beams. Nonlinear Dyn 96(1):647–665

    Google Scholar 

  165. Mi Y, Yu X (2021) Sound transmission of acoustic metamaterial beams with periodic inertial amplification mechanisms. J Sound Vib 499:116009

    Google Scholar 

  166. Barys M, Zalewski R (2018) Analysis of inertial amplification mechanism with smart spring-damper for attenuation of beam vibrations. In: MATEC web of conferences, vol 157, EDP Sciences, p 03002

  167. Barys M, Jensen JS, Frandsen NM (2018) Efficient attenuation of beam vibrations by inertial amplification. Eur J Mech A 71:245–257

    MathSciNet  Google Scholar 

  168. Muhammad S, Wang S, Li F, Zhang C (2020) Bandgap enhancement of periodic nonuniform metamaterial beams with inertial amplification mechanisms. J Vib Control 1077546319895630

  169. Sun F, Dai X, Liu Y, Xiao L (2021) Seismic mitigation performance of periodic foundations with inertial amplification mechanism considering superstructure-foundation interaction. Smart Mater Struct 30(2):025018

    Google Scholar 

  170. Ormondroyd J (1928) The theory of the dynamic vibration absorber. Trans ASME Appl Mech 50:9–22

    Google Scholar 

  171. Raze G, Kerschen G (2021) \(h_{\infty }\) optimization of multiple tuned mass dampers for multimodal vibration control. Comput Struct 248:106485

    Google Scholar 

  172. Hoang N, Fujino Y, Warnitchai P (2008) Optimal tuned mass damper for seismic applications and practical design formulas. Eng Struct 30(3):707–715

    Google Scholar 

  173. Xiang Y, Tan P, He H, Yao H, Zheng X, Yang K (2023) A novel bi-directional rail variable friction pendulum-tuned mass damper (brvfp-tmd). Mech Syst Signal Process 197:110396

    Google Scholar 

  174. Rajana K, Wang Z, Giaralis A (2023) Optimal design and assessment of tuned mass damper inerter with nonlinear viscous damper in seismically excited multi-storey buildings. Bull Earthq Eng 21(3):1509–1539

    Google Scholar 

  175. Wang X, Zhu Z, Au S-K (2023) Bayesian operational modal analysis of structures with tuned mass damper. Mech Syst Signal Process 182:109511

    Google Scholar 

  176. Hosseini Lavassani SH, Kontoni D-PN, Alizadeh H, Gharehbaghi V (2023) Passive control of ultra-span twin-box girder suspension bridges under vortex-induced vibration using tuned mass dampers: a sensitivity analysis. Buildings 13(5):1279

    Google Scholar 

  177. Zuo L, Nayfeh SA (2006) The two-degree-of-freedom tuned-mass damper for suppression of single-mode vibration under random and harmonic excitation

  178. Huang C, Huo L, Li H (2023) Equivalent linearization and parameter optimization of isochronous-pendulum tuned mass damper. Adv Struct Eng 26(2):234–257

    Google Scholar 

  179. Li Z, Xu K, Bi K, Xu L, Han Q (2023) Suppressing wind-induced bending and torsional vibrations of long-span bridges by series-type tuned mass damper inerters (stmdis). In: Structures, vol 48, Elsevier, Amsterdam, pp 918–933

  180. Deastra P, Wagg DJ, Sims ND, Mills RS (2023) Experimental shake table validation of damping behaviour in inerter-based dampers. Bull Earthq Eng 21(3):1389–1409

    Google Scholar 

  181. Wang L, Zhou Y, Shi W, Zhou Y (2023) Seismic response control of a nonlinear tall building under mainshock-aftershock sequences using semi-active tuned mass damper. Int J Struct Stab Dyn 2340027

  182. Zhao F, Wang Z, Bai H, Tang H (2023) Energy harvesting based on flow-induced vibration of a wavy cylinder coupled with tuned mass damper. Energy 282:128584

    Google Scholar 

  183. Wang L, Nagarajaiah S, Zhou Y, Shi W (2023) Experimental study on adaptive-passive tuned mass damper with variable stiffness for vertical human-induced vibration control. Eng Struct 280:115714

    Google Scholar 

  184. Araz O, Elias S, Kablan F (2023) Seismic-induced vibration control of a multi-story building with double tuned mass dampers considering soil-structure interaction. Soil Dyn Earthq Eng 166:107765

    Google Scholar 

  185. Brzeski P, Pavlovskaia E, Kapitaniak T, Perlikowski P (2015) The application of inerter in tuned mass absorber. Int J Non-Linear Mech 70:20–29

    Google Scholar 

  186. Hwang J-S, Kim J, Kim Y-M (2007) Rotational inertia dampers with toggle bracing for vibration control of a building structure. Eng Struct 29(6):1201–1208

    Google Scholar 

  187. Ikago K, Saito K, Inoue N (2012) Seismic control of single-degree-of-freedom structure using tuned viscous mass damper. Earthq Eng Struct Dyn 41(3):453–474

    Google Scholar 

  188. Wang M, Sun F (2018) Displacement reduction effect and simplified evaluation method for sdof systems using a clutching inerter damper. Earthq Eng Struct Dyn 47(7):1651–1672

    Google Scholar 

  189. Pietrosanti D, De Angelis M, Basili M (2017) Optimal design and performance evaluation of systems with tuned mass damper inerter (tmdi). Earthq Eng Struct Dyn 46(8):1367–1388

    Google Scholar 

  190. Marian L, Giaralis A (2014) Optimal design of a novel tuned mass-damper-inerter (tmdi) passive vibration control configuration for stochastically support-excited structural systems. Probab Eng Mech 38:156–164

    Google Scholar 

  191. Brzeski P, Kapitaniak T, Perlikowski P (2015) Novel type of tuned mass damper with inerter which enables changes of inertance. J Sound Vib 349:56–66

    Google Scholar 

  192. Sarkar S, Fitzgerald B (2020) Vibration control of spar-type floating offshore wind turbine towers using a tuned mass-damper-inerter. Struct Control Health Monit 27(1):e2471

    Google Scholar 

  193. Giaralis A, Petrini F (2017) Wind-induced vibration mitigation in tall buildings using the tuned mass-damper-inerter. J Struct Eng 143(9):04017127

    Google Scholar 

  194. Brzeski P, Lazarek M, Perlikowski P (2017) Experimental study of the novel tuned mass damper with inerter which enables changes of inertance. J Sound Vib 404:47–57

    Google Scholar 

  195. Zhang T, Wang W, Li X, Wang B (2023) Vibration mitigation in offshore wind turbine under combined wind-wave-earthquake loads using the tuned mass damper inerter. Renew Energy 216:119050

    Google Scholar 

  196. Su N, Bian J, Peng S, Chen Z, Xia Y (2023) Analytical optimal design of inerter-based vibration absorbers with negative stiffness balancing static amplification and dynamic reduction effects. Mech Syst Signal Process 192:110235

    Google Scholar 

  197. Xu K-F, Zhang Y-W, Niu M-Q, Chen L-Q (2023) Dynamics analysis of a variable stiffness tuned mass damper enhanced by an inerter. Appl Sci 13(3):1404

    Google Scholar 

  198. Dai W, Shi B, Yang J, Zhu X, Li T (2023) Enhanced suppression of longitudinal vibration transmission in propulsion shaft system using nonlinear tuned mass damper inerter. J Vib Control 29(11–12):2528–2538

    MathSciNet  Google Scholar 

  199. Li D, Ikago K, Yin A (2023) Structural dynamic vibration absorber using a tuned inerter eddy current damper. Mech Syst Signal Process 186:109915

    Google Scholar 

  200. Lazar I, Neild S, Wagg D (2014) Using an inerter-based device for structural vibration suppression. Earthq Eng Struct Dyn 43(8):1129–1147

    Google Scholar 

  201. Huo Z, Ding H, Shu Z (2023) Optimal design of tuned inerter eddy current damper. Soil Dyn Earthq Eng 171:107942

    Google Scholar 

  202. Gao H, Wang Z, Jia J, Cheng Z (2023) The negative stiffness electromagnetic tuned inerter damper for damping enhancement of stay cables. Eng Struct 292:116542

    Google Scholar 

  203. Xu T, Li Y, Leng D (2023) Mitigating jacket offshore platform vibration under earthquake and ocean waves utilizing tuned inerter damper. Bull Earthq Eng 21(3):1627–1650

    Google Scholar 

  204. Xu T, Li Y, Lai T, Zheng J (2021) A simplified design method of tuned inerter damper for damped civil structures: theory, validation, and application. Struct Control Health Monit 28:e2798

    Google Scholar 

  205. Deastra P, Wagg D, Sims N, Akbar M (2020) Tuned inerter dampers with linear hysteretic damping. Earthq Eng Struct Dyn 49(12):1216–1235

    Google Scholar 

  206. Zahedin Labaf D, De Angelis M, Basili M (2023) Multi-objective optimal design and seismic assessment of an inerter-based hybrid control system for storage tanks. Bull Earthq Eng 21(3):1481–1507

    Google Scholar 

  207. Suthar SJ, Banerji P (2023) Inerter-assisted pendulum-tuned mass damper for across-wind response control of tall buildings. Eng Struct 291:116489

    Google Scholar 

  208. Fitzgerald B, McAuliffe J, Baisthakur S, Sarkar S (2023) Enhancing the reliability of floating offshore wind turbine towers subjected to misaligned wind-wave loading using tuned mass damper inerters (tmdis). Renew Energy 211:522–538

    Google Scholar 

  209. Ma H, Cheng Z, Shi Z, Marzani A (2023) Structural vibration mitigation via an inertial amplification mechanism based absorber. Eng Struct 295:116764

    Google Scholar 

  210. Mu D, Wang K, Shu H, Lu J (2023) A two-stage inertial amplification tuned mass damper with grounded stiffness element. Mech Adv Mater Struct 30(19):3885–3896

    Google Scholar 

  211. Cheng Z, Palermo A, Shi Z, Marzani A (2020) Enhanced tuned mass damper using an inertial amplification mechanism. J Sound Vib 475:115267

    Google Scholar 

  212. Chowdhury S, Banerjee A, Adhikari S (2023) The optimal configuration of negative stiffness inerter-based base isolators in multi-storey buildings. Structures 50:1232–1251

    Google Scholar 

Download references

Acknowledgements

The authors’ would like to acknowledge the Inspire faculty Grant, Grant number DST/ INSPIRE/04/2018/000052 for partial financial support for the project. SC would like to acknowledge the MHRD grant received from IIT Delhi during the period of this research work.

Author information

Authors and Affiliations

  1. Civil Engineering Department, Indian Institute of Technology Delhi, New Delhi, India

    Sudip Chowdhury & Arnab Banerjee

  2. James Watt School of Engineering, The University of Glasgow, Glasgow, Scotland, UK

    Sondipon Adhikari

Authors
  1. Sudip Chowdhury
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Arnab Banerjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sondipon Adhikari
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sudip Chowdhury.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chowdhury, S., Banerjee, A. & Adhikari, S. A Critical Review on Inertially-Amplified Passive Vibration Control Devices. Arch Computat Methods Eng 31, 2139–2175 (2024). https://doi.org/10.1007/s11831-023-10040-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11831-023-10040-z

Search

Navigation