Skip to main content
SpringerLink
Log in

Dynamic Responses of Beam Deflection Model Using \(\gamma\)-Splines Functions and Fourier Transform Discretization Solvers

  • Original Paper
  • Published:
Archives of Computational Methods in Engineering Aims and scope Submit manuscript

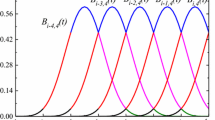
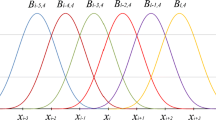
Abstract

Throughout this paper, we use Fourier Transform Discretization (FTD) to solve the dynamic deflection of the beam deformation model. The considered problem is a Partial Differential Equation with non-homogeneous boundary conditions, which expresses the displacement of beam under the effect of an arbitrary moving source force. Our method is usually carried out in two steps. Firstly, the equations and boundary conditions are changed into other equivalent equations and mixed boundary conditions for the frequency parameters. The approximate solution of this last problem is computed using a weak variational analysis technique based on the higher-order Normalized Uniform Polynomial Splines solver. Secondly, several quadrature techniques are employed to calculate the Inverse Fourier Transform of the solution, and then we give a comparison report between the numerous numerical computations of this integral. Careful numerical experiments are presented to indicate the success and well-precious resolution properties for all kinds of smooth and discontinuous solutions and plots of field of displacements of the beam. Similarly, as an application, the FTD and splines finite element methods are employed to solve the coupled Timoshenko transverse vibrating equations with non-homogeneous boundary conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Baruh H (1999) Analytical dynamics. McGraw-Hill, New York

    Google Scholar 

  2. Ferreira AJM (2009) MATLAB codes for finite element analysis: solids and structures, solids mechanics and its applications. Springer, Cham, p 157

    Google Scholar 

  3. Kim Y-W, Cha SC (2018) Finite element formulation and analysis of Timoshenko beam excited by transversely fluctuating supports due to a real seismic wave. Nucl Eng Technol 50:971–980

    Article  Google Scholar 

  4. Andersen L, Nielsen SRK, Kirkegaard PH (2001) Finite element modelling of infinite Euler beams on Kelvin foundations exposed to moving loads in convected co-ordinate. J Sound Vib 241(4):587–604

    Article  MATH  Google Scholar 

  5. Timoshenko SP (1921) On the correction factor for shear of the differential equation for transverse vibrations of bars of uniform cross-section. Philos Mag. https://doi.org/10.1080/14786442108636264

    Article  Google Scholar 

  6. Bhashyam GR, Prathar G (1981) The second frequency spectrum of Timoshenko beams. J Sound Vib 76(3):407–420

    Article  Google Scholar 

  7. Christensen RM (2003) Theory of viscoelasticity. Dover Publications, New York

    Google Scholar 

  8. Han SM, Benaroya H, Wfi T (1999) Dynamic of transversely vibrating beams using four engineering theories. J Sound Vib 225(5):935–988

    Article  MATH  Google Scholar 

  9. Mallik AK, Chandra S, Singh AB (2006) Steady-state response of an elastically supported infinite beam to a moving load. J Sound Vib 291:1148–1169

    Article  Google Scholar 

  10. Nishawala Vinesh V (2011) A Study of Large Deflection of Beams and Plats. Dissertation, Graduate School-New Brunswick, Rutgers, The State of New Jersy

  11. Cai CW, Cheung YK, Chan HC (1988) Dynamic response of infinite continuous. Beams subjected to a moving force an exact method. J Sound Vib 123(3):461–472

    Article  Google Scholar 

  12. Laura PAA, Gutierrez RH (1993) Analysis of Vibrating Timoshenko Beams Using the Method of Differential Quadrature. Shock Vib 1(1):89–93

    Article  Google Scholar 

  13. Addam M (2010) Approximation du Problème de Diffusion en Tomographie Optique et Problème Inverse. Dissertation, LMPA, Université Lille-Nord de France

  14. Addam M, Bouhamidi A, Jbilou K (2010) A numerical method for one-dimensional diffusion problem using Fourier transform and the B-spline Galerkin method. Appl Math Comput 215:4067–4079

    Article  MathSciNet  MATH  Google Scholar 

  15. Schultz MH (1973) Splines analysis. Prentice-Hall, New Jersey

    Google Scholar 

  16. de Boor C (1978) A practical guide to splines. Springer, New York

    Book  MATH  Google Scholar 

  17. Addam M, Bouhamidi A, Heyouni M (2018) On solving an acoustic wave problem via frequency-domain approach and tensorial spline Galerkin method. J Sci Comput 74:1193–1220

    Article  MathSciNet  MATH  Google Scholar 

  18. Schultz MH, Varga RS (1967) L-splines. Num Math 10:345–369

    Article  MATH  Google Scholar 

  19. Quarteroni A, Valli A (1994) Numerical approximation of partial differential equation. Springer, Berlin

    Book  MATH  Google Scholar 

  20. Conway HD (1947) The large deflection of simply supported beams. Philos Mag 38:905–911

    Article  MathSciNet  MATH  Google Scholar 

  21. Yavari A, Nouri M, Mofid M (2002) Discrete element analysis of dynamic response of Timoshenko beams under moving mass. Adv Eng Softw 33:143–153

    Article  MATH  Google Scholar 

  22. Chen YH, Huang YH (2000) Dynamic stiffness of infinite Timoshenko beam of viscoelastic foundation in moving co-ordinate. Int J Num Method Eng 48:1–18

    Article  MATH  Google Scholar 

  23. Lahcen G, Gutierrez RH (1989) Existence et unicité de la solution pour un système de deux. EDP Publ Mat 33:313–327

    Article  MATH  Google Scholar 

  24. Feng H, Cui X, Li G (2012) Static and dynamic analysis of Timoshenko Beam using Nodal integration technique. Int J Appl Mech 4(4):1250045-1–1250045-20

    Article  Google Scholar 

  25. Rosinger HE, Ritchie IG (1977) On Timoshenko’s correction for shear in vibrating isotropic beams. J Phys D Appl Phys 10:1461–1466

    Article  Google Scholar 

  26. Canan Girgin Z, Girgin K (2006) A numerical method for static and free-vibration analysis of non-uniform Timoshenko beam-columns. Can J Civ Eng 33:278–293

    Article  Google Scholar 

  27. Lee SY, Lim SM (1995) Vibrations of elastically restrained non-uniform Timoshenko beams. J Sound Vib 183(3):403–415

    Article  MATH  Google Scholar 

  28. Pradhan KK, Chakraverty S (2013) Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh-Ritz method. Compos Part B 51:175–184

    Article  Google Scholar 

  29. Banerjee JR (2001) Frequency equation and mode shape formulae for composite Timoshenko beams. Compos Struct 51:381–388

    Article  Google Scholar 

  30. Banerjee JR, Williams FW (1996) Exact dynamic stiffness matrix for composite Timoshenko beams with applications. J Sound Vib 194(4):573–585

    Article  MATH  Google Scholar 

  31. Anghel V (2019) Numerical methods for transverse vibration analysis of straight Euler and Timoshenko Beams. INCAS Bull 11(3):15–28

    Article  Google Scholar 

  32. Adjerid S (2002) A posteriori error estimates for fourth-order elliptic problems. Comput Methods Appl Mech Eng 191:2539–2559

    Article  MathSciNet  MATH  Google Scholar 

  33. Majkut L (2009) A posteriori error estimates for fourth-order elliptic problems. J Theo Appl Mech 47(1):193–210

    Google Scholar 

  34. Dawe DJ (1978) A finite element for the vibration analysis of Timoshenko Beams. J Sound Vib 60(l):11–20

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. LSA, ENSAH, Université Abdelmalek Essaadi, Ajdir, BP 03, 32003, Al Hoceima, Morocco

    Mohamed Addam & Ahmed Ben Abdellah

  2. Université Lille-Nord de France, ULCO, LMPA, 62228, Calais-Cedex, France

    Abderrahman Bouhamidi

Authors
  1. Mohamed Addam
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ahmed Ben Abdellah
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abderrahman Bouhamidi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mohamed Addam.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Addam, M., Abdellah, A.B. & Bouhamidi, A. Dynamic Responses of Beam Deflection Model Using \(\gamma\)-Splines Functions and Fourier Transform Discretization Solvers. Arch Computat Methods Eng 30, 2383–2408 (2023). https://doi.org/10.1007/s11831-022-09871-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11831-022-09871-z

Search

Navigation