A note on the solution of water wave scattering problem involving small deformation on a porous channel-bed

Abstract

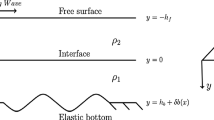
The solution of water wave scattering problem involving small deformation on a porous bed in a channel, where the upper surface is bounded above by an infinitely extent rigid horizontal surface, is studied here within the framework of linearized water wave theory. In such a situation, there exists only one mode of waves propagating on the porous surface. A simplified perturbation analysis, involving a small parameter ε ( ≪ 1), which measures the smallness of the deformation, is employed to reduce the governing Boundary Value Problem (BVP) to a simpler BVP for the first-order correction of the potential function. The first-order potential function and, hence, the first-order reflection and transmission coefficients are obtained by the method based on Fourier transform technique as well as Green’s integral theorem with the introduction of appropriate Green’s function. Two special examples of bottom deformation: the exponentially damped deformation and the sinusoidal ripple bed, are considered to validate the results. For the particular example of a patch of sinusoidal ripples, the resonant interaction between the bed and the upper surface of the fluid is attained in the neighborhood of a singularity, when the ripples wavenumbers of the bottom deformation become approximately twice the components of the incident field wavenumber along the positive x-direction. Also, the main advantage of the present study is that the results for the values of reflection and transmission coefficients are found to satisfy the energy-balance relation almost accurately.