Skip to main content
SpringerLink
Log in

Method for improving RLS algorithms

  • Published:
Journal of Marine Science and Application Aims and scope Submit manuscript

Abstract

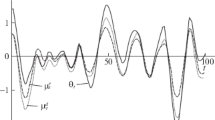
The recursive least-square (RLS) algorithm has been extensively used in adaptive identification, prediction, filtering, and many other fields. This paper proposes adding a second-difference term to the standard recurrent formula to create a novel method for improving tracing capabilities. Test results show that this can greatly improve the convergence capability of RLS algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. BROCKWELL P J, DAVIS R A. Time series: theory and methods[M]. New York: Springer-Verlag Inc, 1991.

    Google Scholar 

  2. SUN Jinghua, JIN Lijun. Application of several improved RLS algorithms in adaptive filter system[J]. Journal of Chongqing University of Posts and Telecommunications, 2003, 15(3): 14–17(in Chinese).

    Google Scholar 

  3. WU Qihui, WANG Jinlong, SHEN Liang, et al. Robust RLS algorithm for adaptive arrays[J]. Acta Electronic Sinica, 2002, 30(6):893–895(in Chinese).

    Google Scholar 

  4. LI Jing, WANG Shuxun, WANG Fei. Parameter estimation of adaptive chirp signal based on polynomial phase transforms[J]. Journal of Jinlin University, 2004, 34(4):617–621(in Chinese).

    Google Scholar 

  5. PARK D, JUN B E. Self-perturbing recursive least squares algorithm with fast tracking capability[J]. Electronics Letters, 1992, 28(6): 558–559.

    Article  Google Scholar 

  6. JIANG J, COOK R. Fast parameter tracking RLS algorithm with high noise immunity[J]. Electronics Letters, 1996, 28(22): 2043–2045.

    Article  Google Scholar 

  7. EOM K, PARK D. Fast tracking and noise-immunized RLS algorithm based on Kalman filter[J]. Electronics Letters, 1996, 32(25):2311–2312.

    Article  Google Scholar 

  8. SO C F, NG S C, LEUNG S H. Gradient based variable forgetting factor RLS algorithm[J]. Signal Processing, 2003, 83: 1163–1175.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Automation, Harbin Engineering University, Harbin, 150001, China

    Tian-shu Li, Kai Tian & Wen-xiu Li

Authors
  1. Tian-shu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kai Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wen-xiu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

LI Tian-Shu was born in 1965. He earned his doctorate from Harbin Engineering University. His current research interests include time series predictions, support vector machines, chaos theory, etc.

TIAN Kai was born in 1972. He is an Associate Professor at Harbin Engineering University. His current research interests include power systems, time series predictions, etc.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Li, Ts., Tian, K. & Li, Wx. Method for improving RLS algorithms. J. Marine. Sci. Appl. 6, 68–70 (2007). https://doi.org/10.1007/s11804-007-5077-x

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11804-007-5077-x

Keywords

CLC number

Search

Navigation