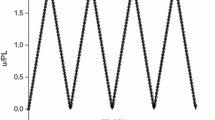
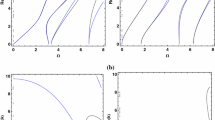
Abstract
Based on the Fourier transform, the analytical solution of boundary integral equations formulated for the complex velocity of a 2-D steady linear surface flow is derived. It has been found that before the radiation condition is imposed, free waves appear both far upstream and downstream. In order to cancel the free waves in far upstream regions, the eigensolution of a specific eigenvalue, which satisfies the homogeneous boundary integral equation, is found and superposed to the analytical solution. An example, a submerged vortex, is used to demonstrate the derived analytical solution. Furthermore, an analytical approach to imposing the radiation condition in the numerical solution of boundary integral equations for 2-D steady linear wave problems is proposed.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Abramowitz, M., and I. A. Stegun, 1972. Handbook of Mathematical Functions. Dover Publications Inc., New York, 1046 pp.
Dawson, C. W., 1977. A practical computer method for solving ship-wave problems. Second Int. Conf. on Numerical Ship Hydrodynamics, Berkeley, 30–38.
Forbes, L. K., 1985a. On the effects of non-linearity in free-surface flow about a submerged point vortex. J. Eng. Math. 19: 139–155.
Forbes, L. K., 1985b. A numerical method for non-linear flow about a submerged hydrofoil. J. Eng. Math., 19: 329–339.
Forbes, L. K., 1984. Irregular frequencies and iterative methods in the solution of steady surface-wave problems in hydrodynamics. J. Eng. Math., 18: 299–313.
Havelock, T. H., 1928. The wave pattern of a doublet in a stream. Proceedings of the Royal Society of London, Series A, 121: 515–523.
Havelock, T. H., 1927. The method of images in some problems of surface waves. Proceedings of the Royal society of London, Series A, 115: 268–279.
Jensen, P.S., 1987. On the numerical radiation condition in the steady-state ship wave problem. J. Ship Res., 31(1): 14–22.
Kochin, N.E., I. A. Kibel, and N.V. Roze, 1964. Theoretical Hydromechanics. Interscience Publishers, New York, 577 pp.
Lalli, F., E. Campana, and U. Bulgarelli, 1992. Numerical simulation of fully-nonlinear steady free surface flow. Intl. J. Numer. Meth. Fluids, 14: 1135–1149.
Lamb, H., 1962. Hydrodynamics. 6th edition. Cambridge University Press, Cambridge, 687 pp.
Scavounos, P.D., and D.E. Nakos, 1988. Stability analysis of panel methods for free-surface flows with forward speed. 17th Symposium on Naval Hydrodynamics, Hague 173–193.
Scullen, D., and E. O. Tuck, 1995. Nonlinear free-surface flow computations for submerged cylinders. J. Ship Res., 39(3): 185–193.
Sneddon, I. N., 1951. Fourier Transforms. McGraw-Hill Book Co., New York, 542 pp.
Wehausen, J.V., and E.V. Laitone, 1960. Surface waves. In: Encyclopedia of Physics, Vol. 19. Springer-Verlag, California, 446–778.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chuang, J.M. Analytical solution of boundary integral equations for 2-D steady linear wave problems. J Ocean Univ. China 4, 357–365 (2005). https://doi.org/10.1007/s11802-005-0057-8
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1007/s11802-005-0057-8