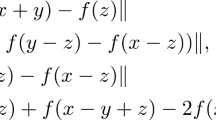Skip to main content

Additive s-functional inequality and hom-derivations in Banach algebras

Journal of Fixed Point Theory and Applications volume 21, Article number: 18 (2019) Cite this article

Abstract

In this paper, we introduce and solve the following additive s-functional inequality:

$$\begin{aligned} \left\| f\left( x+y\right) - f(x )- f(y)\right\| \le \Vert s (f(x-y)-f(x)-f(-y))\Vert , \end{aligned}$$
(0.1)

where s is a fixed nonzero complex number with \(|s|<1\). Using the fixed point method and the direct method, we prove the Hyers–Ulam stability of the additive s-functional inequality (0.1) in complex Banach spaces. Furthermore, we prove the Hyers–Ulam stability of hom-derivations in complex Banach algebras.

This is a preview of subscription content, access via your institution.

Access options

Buy single article

Instant access to the full article PDF.

USD 39.95

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

References

  1. Abdollahpoura, M.R., Aghayaria, R., Rassias, M.T.: Hyers–Ulam stability of associated Laguerre differential equations in a subclass of analytic functions. J. Math. Anal. Appl. 347, 605–612 (2016)

    Article  MathSciNet  Google Scholar 

  2. Aoki, T.: On the stability of the linear transformation in Banach spaces. J. Math. Soc. Jpn. 2, 64–66 (1950)

    Article  MathSciNet  Google Scholar 

  3. Cădariu, L., Radu, V.: Fixed points and the stability of Jensen’s functional equation. J. Inequal. Pure Appl. Math. 4(1), 4 (2003)

  4. Cădariu, L., Radu, V.: On the stability of the Cauchy functional equation: a fixed point approach. Grazer Math. Ber. 346, 43–52 (2004)

    MathSciNet  MATH  Google Scholar 

  5. Cădariu, L., Radu, V.: Fixed point methods for the generalized stability of functional equations in a single variable. Fixed Point Theory Appl. 2008, 749392 (2008)

  6. Chahbi, A., Bounader, N.: On the generalized stability of d’Alembert functional equation. J. Nonlinear Sci. Appl. 6, 198–204 (2013)

    Article  MathSciNet  Google Scholar 

  7. Cholewa, P.W.: Remarks on the stability of functional equations. Aequationes Math. 27, 76–86 (1984)

    Article  MathSciNet  Google Scholar 

  8. Diaz, J., Margolis, B.: A fixed point theorem of the alternative for contractions on a generalized complete metric space. Bull. Am. Math. Soc. 74, 305–309 (1968)

    Article  MathSciNet  Google Scholar 

  9. Eghbali, N., Rassias, J.M., Taheri, M.: On the stability of a \(k\)-cubic functional equation in intuitionistic fuzzy \(n\)-normed spaces. Results Math. 70, 233–248 (2016)

    Article  MathSciNet  Google Scholar 

  10. Gǎvruta, P.: A generalization of the Hyers–Ulam–Rassias stability of approximately additive mappings. J. Math. Anal. Appl. 184, 431–436 (1994)

    Article  MathSciNet  Google Scholar 

  11. Hyers, D.H.: On the stability of the linear functional equation. Proc. Nat. Acad. Sci. USA 27, 222–224 (1941)

    Article  MathSciNet  Google Scholar 

  12. Isac, G., Rassias, ThM: Stability of \(\psi \)-additive mappings: applications to nonlinear analysis. Int. J. Math. Math. Sci. 19, 219–228 (1996)

    Article  MathSciNet  Google Scholar 

  13. Jung, S.-M., Mortici, C., Rassias, MTh: On a functional equation of trigonometric type. Appl. Math. Comput. 252, 294–303 (2015)

    MathSciNet  MATH  Google Scholar 

  14. Jung, S.-M., Popa, D., Rassias, MTh: On the stability of the linear functional equation in a single variable on complete metric groups. J. Glob. Optim. 59, 165–171 (2014)

    Article  MathSciNet  Google Scholar 

  15. Kang, D.: Brzȩk fixed point approach for generalized quadratic radical functional equations. J. Fixed Point Theory Appl. 20, 50 (2018)

    Article  Google Scholar 

  16. Kannappan, P.: Functional Equations and Inequalities with Applications. Springer, Berlin (2009)

    Book  Google Scholar 

  17. Kaskasem, P., Klin-Eam, C., Cho, Y.: On the stability of the generalized Cauchy–Jensen set-valued functional equations. J. Fixed Point Theory Appl. 20, 76 (2018)

    Article  MathSciNet  Google Scholar 

  18. Lee, Y.-H., Jung, S.-M., Rassias, MTh: Uniqueness theorems on functional inequalities concerning cubic-quadratic-additive equation. J. Math. Inequal. 12, 43–61 (2018)

    Article  MathSciNet  Google Scholar 

  19. Lee, Y.-H., Jung, S.-M., Rassias, MTh: On an n-dimensional mixed type additive and quadratic functional equation. Appl. Math. Comput. 228, 13–16 (2014)

    MathSciNet  MATH  Google Scholar 

  20. Miheţ, D., Radu, V.: On the stability of the additive Cauchy functional equation in random normed spaces. J. Math. Anal. Appl. 343, 567–572 (2008)

    Article  MathSciNet  Google Scholar 

  21. Mirzavaziri, M., Moslehian, M.S.: Automatic continuity of \(\sigma \)-derivations on \(C^*\)-algebras. Proc. Am. Math. Soc. 134, 3319–3327 (2006)

    Article  MathSciNet  Google Scholar 

  22. Mirzavaziri, M., Moslehian, M.S.: \(\sigma \)-derivations in banach algebras. Bull. Iran. Math. Soc. 32, 65–78 (2007)

    MathSciNet  MATH  Google Scholar 

  23. Park, C.: Homomorphisms between Poisson \(JC^*\)-algebras. Bull. Braz. Math. Soc. 36, 79–97 (2005)

    Article  MathSciNet  Google Scholar 

  24. Park, C.: Additive \(\rho \)-functional inequalities and equations. J. Math. Inequal. 9, 17–26 (2015)

    Article  MathSciNet  Google Scholar 

  25. Park, C.: Additive \(\rho \)-functional inequalities in non-Archimedean normed spaces. J. Math. Inequal. 9, 397–407 (2015)

    Article  MathSciNet  Google Scholar 

  26. Park, C.: Fixed point method for set-valued functional equations. J. Fixed Point Theory Appl. 19, 2297–2308 (2017)

    Article  MathSciNet  Google Scholar 

  27. Radu, V.: The fixed point alternative and the stability of functional equations. Fixed Point Theory 4, 91–96 (2003)

    MathSciNet  MATH  Google Scholar 

  28. Rassias, ThM: On the stability of the linear mapping in Banach spaces. Proc. Am. Math. Soc. 72, 297–300 (1978)

    Article  MathSciNet  Google Scholar 

  29. Skof, F.: Propriet locali e approssimazione di operatori. Rend. Sem. Mat. Fis. Milano 53, 113–129 (1983)

    Article  MathSciNet  Google Scholar 

  30. Ulam, S.M.: A Collection of the Mathematical Problems. Interscience Publ, New York (1960)

    MATH  Google Scholar 

  31. Wang, Z.: Stability of two types of cubic fuzzy set-valued functional equations. Results Math. 70, 1–14 (2016)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This research was supported by the Daejin University Research Grant.

Author information

Authors and Affiliations

  1. Research Institute for Natural Sciences, Hanyang University, Seoul, 04763, Republic of Korea

    Choonkil Park

  2. Department of Mathematics, Daejin University, Kyunggi, 11159, Republic of Korea

    Jung Rye Lee

  3. Department of Mathematics, School of Arts and Sciences, Shaanxi University of Science and Technology, Xi’an, People’s Republic of China

    Xiaohong Zhang

  4. Department of Mathematics, College of Arts and Sciences, Shanghai Maritime University, Shanghai, People’s Republic of China

    Xiaohong Zhang

Authors
  1. Choonkil Park
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jung Rye Lee
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiaohong Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jung Rye Lee.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Park, C., Lee, J.R. & Zhang, X. Additive s-functional inequality and hom-derivations in Banach algebras. J. Fixed Point Theory Appl. 21, 18 (2019). https://doi.org/10.1007/s11784-018-0652-0

Download citation

  • Published:

  • DOI: https://doi.org/10.1007/s11784-018-0652-0

Keywords

  • Hyers–Ulam stability
  • hom-derivation in Banach algebra
  • additive s-functional inequality
  • fixed point method
  • direct method

Mathematics Subject Classification

  • Primary 39B62
  • 47H10
  • 39B52
  • 47B47
  • 46L57