Skip to main content
SpringerLink
Log in

Wing crack model subjected to high hydraulic pressure and far field stresses and its numerical simulation

  • Published:
Journal of Central South University Aims and scope Submit manuscript

Abstract

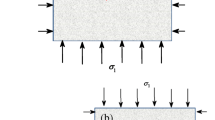
By considering the effect of hydraulic pressure filled in wing crack and the connected part of main crack on the stress intensity factor at wing crack tip, a new wing crack model exerted by hydraulic pressure and far field stresses was proposed. By introducing the equivalent crack length l eq of wing crack, two terms make up the stress intensity factor K I at wing crack tip: one is the component K (1)I for a single isolated straight wing crack of length 2l subjected to hydraulic pressure in wing crack and far field stresses, and the other is the component K (2)I due to the effective shear stress induced by the presence of the equivalent main crack. The FEM model of wing crack propagation subjected to hydraulic pressure and far field stresses was also established according to different side pressure coefficients and hydraulic pressures in crack. The result shows that a good agreement is found between theoretical model of wing crack proposed and finite element method (FEM). In theory, an unstable crack propagation is shown if there is high hydraulic pressure and lateral tension. The wing crack model proposed can provide references for studying on hydraulic fracturing in rock masses.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. CAI M. Influence of intermediate principal stress on rock fracturing and strength near excavation boundaries-Insight from numerical modeling [J]. International Journal of Rock Mechanics & Mining Sciences, 2008, 45: 763–772.

    Article  Google Scholar 

  2. SAHOURYEH E, DYSKIN A V, GERMANOVICH L N. Crack growth under biaxial compression [J]. Eng Fract Mech, 2002, 69(18): 2187–2198.

    Article  Google Scholar 

  3. CAI M, KAISER P K. Assessment of excavation damaged zone using micromechanics model [J]. Tunnelling and Underground Space Technology, 2005, 20(4): 301–310.

    Article  Google Scholar 

  4. ASHBY M F, SAMMIS. The damage mechanics of brittle solids in compression [J]. Pageoph, 1990, 133(3): 489–518.

    Article  Google Scholar 

  5. HORII H, NEMAT-NASSER S. Compression-induced microcrack growth in brittle solids: Axial splitting and shear failure [J]. J Geophys Res, 1985, 90: 3105–3125.

    Article  Google Scholar 

  6. HORII H, NEMAT-NASSER S. Brittle failure in compression: Splitting, faulting and brittle-ductile transition [J]. Phil Trans R. Soc Lond A, 1986, 139: 337–374.

    Google Scholar 

  7. ASHBY M F, HALLAM S D. The failure of brittle solids containing small cracks under compressive stress states [J]. Acta Metall, 1986, 34: 497–510.

    Article  Google Scholar 

  8. STEIF P S. Crack extension under compressive loading [J]. Engng Fract Mech, 1984, 20: 463–473.

    Article  Google Scholar 

  9. BAUD P, REUSCHLE T, CHARLEZ P. An improved wing crack model for the deformation and failure of rock in compression [J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1996, 33(5): 539–542.

    Article  Google Scholar 

  10. WANG Yuan-han, XU Yue, TAN Guo-hua. An improved calculative model for wing crack [J]. Chinese Journal of Geotechnical Engineering, 2000, 22(5): 612–615. (in Chinese)

    Google Scholar 

  11. NAKASHIMA Y. Buoyancy-driven propagation of an isolated fluid-filled crack in rock: Implication for fluid transport in metamorphism [J]. Contributions to Mineralogy and Petrology, 1993, 11(4): 289–295.

    Article  Google Scholar 

  12. TANG Lian-sheng, ZHANG Peng-cheng, WANG Si-jing. Testing study on effects of chemical action of aqueous solution on crack propagation in rock [J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(6): 822–827. (in Chinese)

    Google Scholar 

  13. ZHUANG Ning. Propagation rule of crack rock mass and its mathematics model research under the hydraulic-stress coupling [D]. Shanghai: TongJi University, 2006: 111–112. (in Chinese)

  14. KATSUMI, N, HIROKAZU M, HIROAKI, N, NORIYOSHI T. Mechanical and hydraulic coupling of injection-induced slip along pre-existing fractures [J]. Geothermics, 2008, 37: 157–172.

    Article  Google Scholar 

  15. LEE M Y, HAIMSON B C. Statistical evaluation of hydraulic fracturing stress measurement parameters [J]. Int J Rock Mech Min, Sci & Geomech Abstr, 1989, 26: 447–56.

    Article  Google Scholar 

  16. LUO Xiao-rong, VASSEUR G. Natural hydraulic cracking: numerical model and sensitivity study [J]. Earth and Planetary Science Letters, 2002, 20(1): 431–446.

    Article  Google Scholar 

  17. PAPANASTASIOU P C. A coupled elastoplastic hydraulic fracturing model [J]. Int J Rock Mech & Min Sci, 1997, 34: 3–4.

    Article  Google Scholar 

  18. ZHAO Y L, CAO P, WANG W J. Viscoelasto-plastic rheological experiment under circular increment step load and unload and nonlinear creep model of soft rocks [J]. Journal of Central South University of Technology, 2009, 16(3): 484–491.

    Google Scholar 

  19. LAUTERBACH B, GROSS D. Crack growth in brittle solids under compression [J]. Mechanics of Materials, 1998, 29: 81–92.

    Article  Google Scholar 

  20. LEE S, RABICHANDRAN G. Crack initiation in brittle solids under multiaxial compression [J]. Engineering Fracture Mechanics, 2003, 70: 1645–1658.

    Article  Google Scholar 

  21. DYSKIM A V, SAHOURYEH E, JEWELL R J, JOER J H, USTINOV K B. Influence of shape and locations of initial 3-D cracks on their growth in uniaxial compression [J]. Engineering Fracture Mechanics, 2003, 70: 2115–2136.

    Article  Google Scholar 

  22. SAHOURYEH E, DYSKIM A V, GERMANOVICH L N. Crack growth under biaxial compression [J]. Engineering Fracture Mechanics, 2002, 69: 2187–2198.

    Article  Google Scholar 

  23. YU Xiao-zhong. Fracture mechanics of rock and concrete [M]. Changsha: Central South University of Technology Press, 1991: 20–21. (in Chinese)

    Google Scholar 

  24. AYATOLLAHI M R, ALIHA M R M. Wide range data for crack tip parameters in two disc-type specimens under mixed model loading [J]. Computational Materials Science, 2007, 38(4): 660–670.

    Article  Google Scholar 

  25. ZHAO Yan-lin, CAO Ping, WEN You-dao. Damage fracture failure mechanism of compressive-shear rock cracks under seepage pressure [J]. Journal of Central South University: Science and Technology, 2008, 39(4): 838–844. (in Chinese)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Energy and Safety Engineering, Hunan University of Science and Technology, Xiangtan, 411201, China

    Yan-lin Zhao  (赵延林), Wei-jun Wang  (王卫军) & Wen Wan  (万文)

  2. Hunan Provincial Key Laboratory of Safe Mining Techniques of Coal Mines, Hunan University of Science and Technology, Xiangtan, 411201, China

    Yan-lin Zhao  (赵延林), Wei-jun Wang  (王卫军) & Wen Wan  (万文)

  3. School of Resources and Safety Engineering, Central South University, Changsha, 410083, China

    Yan-lin Zhao  (赵延林), Ping Cao  (曹平) & Rui Chen  (陈锐)

Authors
  1. Yan-lin Zhao  (赵延林)
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ping Cao  (曹平)
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei-jun Wang  (王卫军)
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Wen Wan  (万文)
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Rui Chen  (陈锐)
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yan-lin Zhao  (赵延林).

Additional information

Foundation item: Projects(10972238, 51074071, 50974059) supported by the National Natural Science Foundation of China; Project(10JJ3007) supported by the Natural Science Foundation of Hunan Province, China; Project(11C0539) supported by Scientific Research Fund of Hunan Provincial Education Department, China; Project(200905) supported by Open Research Fund of Hunan Provincial Key of Safe Mining Techniques of Coal Mines, China

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhao, Yl., Cao, P., Wang, Wj. et al. Wing crack model subjected to high hydraulic pressure and far field stresses and its numerical simulation. J. Cent. South Univ. Technol. 19, 578–585 (2012). https://doi.org/10.1007/s11771-012-1042-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11771-012-1042-1

Key words

Search

Navigation