Robust and fault-tolerant spacecraft attitude control based on an extended-observer design

Abstract

The aim of this work is to develop a robust control strategy able to drive the attitude of a spacecraft to a reference value, despite the presence of unknown but bounded uncertainties in the system parameters and external disturbances. Thanks to the use of an extended observer design, the proposed control law is robust against all the uncertainties that affect the high-frequency gain matrix, which is shown to capture a broad spectrum of modelling issues, some of which are often neglected by traditional approaches. The proposed controller then provides robustness against parametric uncertainties, as moment of inertia estimation, payload deformations, actuator faults and external disturbances, while maintaining its asymptotic properties.

1 Introduction

Attitude is one of the fundamental components of spacecraft operations, as it governs the most crucial aspect of the typical space missions: the pointing. Attitude control has been studied extensively in the aerospace field, becoming one of the classic control problems [1] not only for its real-world implications but also for its complexity. Having to control a device whose life-span can be well over a decade and which is subject to significant uncertainties, disturbances and faults, robust control naturally gained the attention of the scientific community, as it is able to maintain the asymptotic properties needed to successfully complete the mission even under actual, non-ideal, conditions.

The control law presented in this paper is based on the extended-observer paradigm introduced in [2], and extended to the MIMO domain in [3], and has been developed with the goal of providing resiliency to the spacecraft operation with respect to (i) modelling uncertainties, (ii) deformations and faults and (iii) external disturbances, while also taking in consideration the physical limitations of the system, in the form of the saturation of the actuators.

Utilizing a control law of this type allows to extend the operational life of the spacecraft, which in turn reduces the amount of space debris, one of the main challenges of modern space campaigns [4], and increases the economical return of the launch campaign. The proposed control law will be shown to reconstruct a control law designed neglecting the presence of uncertainties, simplifying the spacecraft operator mission planning.

The paper is organized as follows: Sect. 2 contains a brief review of the state-of-the-art and highlights the paper main contributions; Sect. 3 reports the needed prelaminar notions on attitude control, normal forms for nonlinear systems and spacecraft modelling; Sect. 4 covers the design of the extended observer and its application for the development of the utilized control law; Sect. 5 contains the results of numerical simulations to validate the proposed control approach; Sect. 6 draws the conclusions and outlines future research lines.

Main symbols
$\times , \ \cdot , \otimes$	Vector, scalar and quaternion cross products
$e,\theta$	Euler’s axis and angle
$I_{n}$	$(n \times n)$ identity matrix
J	MOI tensor in the rigid body reference frame (kg$\,\cdot \,$m$^{2}$)
$(I_{x},I_{y},\ I_{z})$	Principal MOI (kg$\,\cdot \,$m$^{2}$)
$L_{\tau }$	Distribution matrix
${\mathcal {L}}_{f}h(x)$	Lie derivative of h(x) along f
$q,q_{13},q_{4}$	Quaternion representation of the attitude, vector and scalar components of the quaternion
$u = L_{\tau }\tau$	Control signal, control torques over the principal axes of the spacecraft (N)
$\omega$	Angular velocity of the inertial reference frame relative to the satellite measured in its coordinates (rad/s)
$\tau$	Torques applied by the reaction wheels (N)
$\tau ^{\mathrm{ext}}$	External torques over the principal axes of the spacecraft (N)

2 State-of-the-art review and paper contribution

The problem of attitude control for a rigid body has found broad applications in aerospace [5], and due to its impact on the spacecraft successful operation, the available literature covers several different research directions, spacing from optimal control [6] to model predictive control [7] and fuzzy-logic based controllers [8].

In particular, the field of robust control has always been of particular interest for both industry and academia, as a spacecraft is a very complex system whose physical characteristics can vary over time—e.g., its Moment of Inertia (MOI) depends on the remaining propellant and configuration of its solar panels and manipulators—and are subject to significant uncertainties, also due to the heavy stress which the spacecraft is exposed to during its launch [9].

Several works as [10,11,12,13,14,15], developed control laws, based on the measurements of both attitude and angular velocity of the spacecraft, which provide robustness with respect to uncertain inertia characteristics of the spacecraft, which in some cases is estimated by the controller itself [12, 14].

This work, as [16,17,18], presents a dynamic control law that is based only on attitude measurements while additionally providing robustness against uncertainties affecting the knowledge both of the inertia moment of the spacecraft and its actuators positioning and operativeness.

The robust control methods studied have naturally been paired with disturbance rejection controllers, as a spacecraft is typically subject to non-negligible external torques [19], and several works, as [13,14,15], present both properties. Other than the already mentioned robustness with respect to the inertial estimation, Sanyal et al. [14] presented a nonlinear control that rejects constant disturbances and sinusoidal ones, having only information on the disturbance frequency. Similarly, Liu et al. [15] introduced a $\mathrm{H}_{\infty }$ controller that is able to address inertial uncertainties, external disturbances, gyro drifts and control perturbations. In [13] a control law, based on the internal model principle, is designed specifically for a low earth orbit (LEO) satellite, that is characterized by the presence of significant disturbance torques, caused by aerodynamic drag. This work focuses on uncertainties that affect the high frequency gain of the spacecraft system, which, as will be discussed, capture parametric uncertainties not only on the moment of inertia, enabling the rejection of control perturbations. For the properties of the proposed extended observer, the control designed in this paper will also be able to reject constant disturbances, while also being able to arbitrarily attenuate sinusoidal ones.

Other than robustness, a successful spacecraft controller should also take into account the resiliency of the system operation with respect to faults occurring on either its actuators or the available sensors. Regarding noise and malfunctioning on measurements, typical solutions are based on Kalman filtering [20] and sensor redundancy.

Regarding actuators, the typical components utilized for attitude control are momentum wheels and control moment gyroscopes. Both typologies of actuators are expensive in price and mass terms, and, due to their spinning nature and frequent usage, are sensible to total and partial faults. For this reason fault tolerant control schemes are commonly utilized in the industry [21]. As will be discussed, this paper considers a satellite in which a standard configuration for actuator redundancy has been implemented to be resilient against a complete failure of one of its actuators, but as in [22] it develops a law that rejects the effect of partial faults effecting, potentially, all its actuators at the same time.

Another crucial aspect to consider is the physical limitation of the actuators, which translates into control saturations. In this regard, both authors in [23] and [24] presented robust full-state feedback controllers that address control saturations. In particular, Boskovic et al. [23] introduced a nonlinear dynamic control law that can successfully govern the attitude of a spacecraft under inertial uncertainties, external disturbances and input saturations, while Xiao et al. [24] extended the results of [23] considering also the possibility of actuator faults, as does this work.

Robust and fault tolerant attitude control schemes have also been broadly explored in the multi-spacecraft setting, where a set of satellites/spacecrafts seek some form of coordination or formation control. Distributed observers were studied in works such as [25], where a leader-following scheme was developed, and [26,27,28], where distributed estimation schemes were designed for formation control.

We mention that, over the last few years, a significant research effort has been spent regarding the development of data-driven solutions able to cope with the robustness and fault-tolerant aspects presented above. Such solutions, typically propose learning schemes to infer/identify unmodeled system dynamics or estimation errors and then use the discovered information to reconstruct effective control policies. For instance, authors in [29,30,31,32,33] proposed data-driven control schemes for attitude stabilization that were, in certain cases, successfully tested on real-world helicopters and quadrotors, demonstrating robust performances against external disturbances and parameter uncertainties. The main advantage that model-based solutions, as the one presented in this work, have against data-driven approaches is the absence of a training phase, during which the controller interacts with the physical system in a black-box fashion, meaning that they may be deployed more easily in the field. Another aspect in favour of model-based solutions for spacecraft applications is their intrinsic explainability, that is the fact that, due to the availability of closed-form equations that determine the control law, one may always oversee and predict how the system will behave in a given environment.

A significant advantage that the control scheme presented in this paper has compared to most of the available literature is the ability of the controller to reconstruct any arbitrary control law that could have been designed to govern the attitude of a spacecraft under feedback linearization. In other words, the proposed controller allows to design a control law to fulfil the spacecraft mission, as one was in absence of model uncertainties (affecting either moment of inertia estimation and payload deformation), actuator operativeness (either partial or complete faults) and external disturbances (either constant or time varying). Due to the asymptotic control law reconstruction, the controller proposed also recovers the transient performances that motivated the design of the control law for the feedback linearized system.

As it will be discussed, the only assumptions that the controller requires are the ones of feedback linearization (i.e., the mission should avoid the quaternion singularity $q_{4} = 0$), and the availability of an estimation of the high frequency gain, that translates into providing the controller with a reasonable estimation of its current moment of inertia and actuator configuration.

3 Preliminaries

This section summarizes notions on satellite attitude control (Sect. 3.1), normal forms (Sect. 3.2) and on the extended observed paradigm (Sect. 3.3).

3.1 Preliminaries on satellite attitude control

In order to represent the attitude of a rigid body there exist several representations, ranging from Euler angles and rotation matrices to the so-called Rodrigues parameters [34]. One of the most broadly used representations for spacecraft attitude is the unitary quaternion one. Let the quaternion q be defined as $q = \begin{bmatrix} q_{13} \\ q_{4} \\ \end{bmatrix} \in {\mathbb {R}}^{4}$, in which $q_{13} \in {\mathbb {R}}^{3}$ and $q_{4}{\in {\mathbb {R}}}$, such that the unitary norm property $\Vert q \Vert = 1$ holds.

We can link this attitude representation to the Euler axis and angle $(\varsigma ,\theta )\$with the simple transformation [35]:

$$\begin{aligned} q = \left[ \begin{aligned} \varsigma ~\sin \dfrac{\theta }{2} \\ \cos \dfrac{\theta }{2}~~\\ \end{aligned}\right] . \end{aligned}$$

(1)

Let $\times$ be the vector cross product. We define for convenience the operator

$$\begin{aligned}{}[q \times ]= \left[q_{13} \times \right]= \begin{bmatrix} 0 &{} - q_{3} &{} q_{2} \\ q_{3} &{} 0 &{} - q_{1} \\ - q_{2} &{} q_{1} &{} 0 \\ \end{bmatrix}\end{aligned}$$

and the quaternion cross product [36]

$$\begin{aligned} q^{1} \otimes q^{2} = \begin{bmatrix} q_{4}^{2}q_{13}^{1} + q_{4}^{1}q_{13}^{2} - q_{13}^{1} \times q_{13}^{2} \\ q_{4}^{1}q_{4}^{2} - q_{13}^{1} q_{13}^{2} \\ \end{bmatrix}, \end{aligned}$$

and we introduce the following operator:

$$\begin{aligned}{}[q \otimes ]= \begin{bmatrix} q_{4}I_{3} - \left[q_{13} \times \right]&{} \ q_{13} \\ - q_{13}^{\mathrm{T}} &{} q_{4} \\ \end{bmatrix}. \end{aligned}$$

(2)

For the sake of notation, when (2) is applied to a vector $x \in {\mathbb {R}}^{3}$ we assume

$$\begin{aligned}x \otimes q = \begin{bmatrix} x \\ 0 \\ \end{bmatrix} \otimes q = [x \otimes ]q.\end{aligned}$$

Finally, we remark the expressions for the conjugate and the inverse quaternions:

$$\begin{aligned}{\overline{q}} = \begin{bmatrix} - q_{13} \\ q_{4} \\ \end{bmatrix},\ q^{- 1} = \dfrac{{\overline{q}}}{{\Vert q\Vert }^{2}}.\end{aligned}$$

Starting from the model of the rigid spacecraft, we can derive, based on the quaternion kinematics and from the rigid body dynamics - as customary in the literature [36]—the following model of the spacecraft:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{q}} = \dfrac{1}{2}\ [\omega \otimes ]q, \\ {\dot{\omega }} = J^{- 1}\left[\tau ^{\mathrm{ext}} + L_{\tau }\tau - \omega \times (J\omega ) \right], \\ \end{array}\right. } \end{aligned}$$

(3)

where $x = \begin{bmatrix} q \\ \omega \\ \end{bmatrix}$; $\omega = \left[\omega _{x},\ \omega _{y},\ \omega _{z} \right]^{\mathrm{T}}$ is the angular velocity vector of the rigid body; $\tau$ is the vector of the control torques provided by the reaction wheels mounted on the spacecraft; $L_{\tau }$ is their distribution matrix as discussed below; $\tau ^{\mathrm{ext}}$ represents the disturbance torques, such as solar radiation, gravity gradient ad magnetic torques [37, 38]; and finally, J is the MOI tensor, expressed, as customary, in the rigid body reference frame. Under dynamics (3), q evolves in such a way that unitary norm property always holds, since

$$\begin{aligned} \vert {\dot{q}} \vert&= {{\dot{q}}}^{\mathrm{T}}q + q^{\mathrm{T}}{\dot{q}} \\&= \dfrac{1}{2}( [\omega \otimes ]q )^{\mathrm{T}}q + \dfrac{1}{2}q^{\mathrm{T}}( [\omega \otimes ]q ) \\&= \dfrac{1}{2}( [\omega \otimes ]q )^{\mathrm{T}}q - \dfrac{1}{2}( [\omega \otimes ]q )^{\mathrm{T}}q = 0. \end{aligned}$$

The typical attitude regulation problem consists in stabilizing (3), as with trivial coordinate transformations or by the introduction of the so-called error quaternions [39], the stabilization of any arbitrary attitude can be reconducted to the stabilization of the origin of (3).

The distribution matrix $L_{\tau }$ plays a particularly crucial role, as it projects the control torques $\tau$ over the principal rigid body inertial axes [40]. It follows that, if $n_{w} > 3$ reaction wheels are mounted, one can independently control the three resulting torques affecting the principal inertial axes as long as $\mathrm{rank}( L_{t} ) = 3$. For this reason, $u = L_{\tau }\tau$ represents a typical choice for the control signal of system (3).

For its projection nature, it is worth remarking that the structure of $L_{\tau }$ is

$$\begin{aligned} L_{\tau } = \left[a_{1}~~a_{2}~~a_{3}~\cdots ~a_{n_{w}} \right], \end{aligned}$$

(4)

in which the column $a_{i} \in {\mathbb {R}}^{3}$ indicates the direction of the axis of the i-th reaction wheel, measured over its principal axes of inertia. The rank property has also implications for fault-tolerant control, since the condition $\mathrm{rank}( L_{t} ) = 3$ can be maintained even in case of the failure of one or more actuators—the complete fault of the i-th actuator modifies the matrix $L_{\tau }$ by substituting its i-th column with a vector of zeros.

Once the control u has been computed, its actuation requires that it is redistributed over the available reaction wheels. A common solution is to use the pseudo-inverse of $L_{\tau }$, defined as $L_{\tau }^{\#} :=$ ${L_{\tau }^{\mathrm{T}}( L_{\tau }\ L_{\tau }^{\mathrm{T}} )}^{- 1}$.

The resulting control torque vector is then

$$\begin{aligned} \tau = L_{\tau }^{\#}u. \end{aligned}$$

(5)

3.2 Preliminaries on normal forms

If we consider a multi-input multi-output (MIMO) system with m inputs and m outputs of the form

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}} = f(x) + \textstyle \sum \limits _{i = 1}^{m}{g_{i}(x)u_{i}}, \\ y = h(x), \end{array}\right. } \end{aligned}$$

(6)

in which $x(t) \in {\mathbb {R}}^{n}$, $u(t) \in {\mathbb {R}}^{m}$, $y(t) \in {\mathbb {R}}^{m}$,

$$\begin{aligned}&f(x) = \left[f_{1}(x),\cdots ,f_{n}(x) \right]', \\&h(x) = \left[h_{1}(x),\cdots ,h_{m}(x) \right]'. \end{aligned}$$

It is well known that, if it has a well-defined vector of relative degree $\{ r_{1},r_{2},\cdots ,r_{m}\}$ in $x_{0}$ [41], there exists a diffeomorphism T(x) that transforms system (6) into the so-called Byrnes-Isidori normal form around $x_{0}$:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{\xi }} = A\xi + B\left[a(\xi ,\eta ) + b(\xi ,\eta )u \right], \\ {\dot{\eta }} = z(\xi ,\eta ), \\ y = C\xi , \end{array}\right. } \end{aligned}$$

(7)

in which $\xi \in {\mathbb {R}}^{r}$, with $r = \ r_{1} + r_{2} + \cdots + r_{m}$, $A = \mathrm{diag}\{ A_{1},\cdots ,A_{m} \}$, $B = \mathrm{diag}\{ B_{1},\cdots ,B_{m} \}$, $C =$ $\mathrm{diag}\{ C_{1},\cdots ,\ C_{m} \}$,

$$\begin{aligned} A_{i} = \left[ \begin{array}{c@{~~}c@{~~}c@{~~}c@{~~}c} 0 &{} 1 &{} 0 &{} \cdots &{} 0 \\ 0 &{} 0 &{} 1 &{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \vdots &{} &{} \vdots \\ 0 &{} 0 &{} 0 &{} \cdots &{} 1 \\ 0 &{} 0 &{} 0 &{} \cdots &{} 0 \\ \end{array}\right] \in {\mathbb {R}}^{r_{i} \times r_{i}}, \end{aligned}$$

$$\begin{aligned} B_{i} = \begin{bmatrix} 0 \\ \vdots \\ 1 \\ \end{bmatrix} \in {\mathbb {R}}^{r_{i} \times 1}, ~~C_{i} = \begin{bmatrix} 1 &{} 0 &{} \begin{matrix} \cdots &{} 0 \\ \end{matrix} \\ \end{bmatrix}. \end{aligned}$$

In (7), $a(\xi ,\eta ):{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{r}$, $b(\xi ,\eta ):{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{r \times m}$ and $z(\xi ,\eta ):{\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{r - n}$ are smooth maps. $z(\xi ,\eta )$ is referred to as the zero-dynamics [42] of system (7).

For the existence of the vector of relative degree in $x_{0}$, system (6) must satisfy two conditions: ${\mathcal {L}}_{g_{j}}{\mathcal {L}}_{f}^{k}h_{i}(x) = 0$, for all $x\mathcal {\in B}( x_{0} )$ and for all j, i, k such that 1$\le j \le m,$ $1 \le i \le m,1< k < r_{j} - 1$; the decoupling matrix

$$\begin{aligned}\varDelta (x) = \begin{bmatrix} {\mathcal {L}}_{g_{1}}{\mathcal {L}}_{f}^{r_{1} - 1}h_{1}(x) &{} \cdots &{} {\mathcal {L}}_{g_{m}}{\mathcal {L}}_{f}^{r_{1} - 1}h_{1}(x) \\ \vdots &{} &{} \vdots \\ {\mathcal {L}}_{g_{1}}{\mathcal {L}}_{f}^{r_{m} - 1}h_{m}(x) &{} \cdots &{} {\mathcal {L}}_{g_{m}}{\mathcal {L}}_{f}^{r_{m} - 1}h_{m}(x) \\ \end{bmatrix}\end{aligned}$$

is nonsingular in$\ x_{0}$.

Ideally, under these conditions, the system (7) is stabilized by applying a linearizing control of the form

$$\begin{aligned} u = b^{- 1}(\xi ,\eta )( K\xi - a(\xi ,\eta ) ) \end{aligned}$$

(8)

with K such that $(A + BK)$ is Hurwitz. It is worth remarking that the selection of K is what determines the performances of the controlled system, in terms of its transient behaviour. In particular, K can be chosen following standard procedures for transient response shaping, such as pole-placement or LQR.

Note that (8) requires the precise knowledge of the system model, specifically to implement the exact cancellation of the term $a(\xi ,\eta )$ in (7).

3.3 Preliminaries on the extended observer

In this paper, we will control system (3) utilizing a dynamical output-feedback control based on an extended-observer paradigm, introduced in [2, 43] and extended to the MIMO domain in [3].

The extended observer is implemented by the following dynamical system:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{\hat{\xi }}}_{i,1} = {\hat{\xi }}_{i,2} + \kappa \alpha _{i,1}( y_{i} - {\hat{\xi }}_{i,1} ), \\ {\dot{\hat{\xi }}}_{i,2} = \sigma _{i} + {\varvec{b}}_{i}u^{*} + \kappa ^{2}\alpha _{i,2}( y_{i} - {\hat{\xi }}_{i,1} ), \\ \dot{\sigma _{i}} = \kappa ^{3}\alpha _{i,3}( y_{i} - {\hat{\xi }}_{i,1} ), \\ \end{array}\right. }\ i = 1,2,3, \end{aligned}$$

(9)

in which $\kappa$ and $\alpha _{i,1},\ \cdots ,\ \alpha _{i,3}$ are design parameters, ${\hat{\xi }}_{i,1}$, ${\hat{\xi }}_{i,2}$ and $\sigma _{i},$ are the state variables of the observer and ${\varvec{b}}_{i} \in {\mathbb {R}}^{3}$ is the i-th row of the constant matrix ${\varvec{b}} \in {\mathbb {R}}^{3 \times 3}$, $i = 1,2,3$.

The structure of (9) is the one of a typical high-gain observer, with the vector ${\hat{\xi }} = \mathrm{col}( {\hat{\xi }}_{1,1},\cdots ,{\hat{\xi }}_{3,2} )$ estimating of the state $\xi$ of the system, with the addition of a new variable vector, $\sigma = \mathrm{col}( \sigma _{1},\cdots ,\ \sigma _{3} )$, that will be used to attain the robustness of the control. Differently to standard high-gain observers, the extended observer (9) is also used to compute the robustly stabilizing control law

$$\begin{aligned} u^{*} = G_{H}( {\varvec{b}}^{- 1}[K{\hat{\xi }} - \sigma ]) \end{aligned}$$

(10)

with $G_{H}(s):{\mathbb {R}}^{3} \rightarrow {\mathbb {R}}^{3}$ defined as

$$\begin{aligned}G_{H}(s) = \mathrm{col}( g_{H}( s_{1} ),g_{H}( s_{2} ),g_{H}( s_{3} ) ),\end{aligned}$$

where $g_{H}(s){:{\mathbb {R}} \rightarrow {\mathbb {R}}}$ is a smooth saturation function such that:

• $g_{H}(s) = s$ if $\vert s\vert \le H$;

• $g_{H}(s)$ is odd and monotonically increasing, with $0 \le \frac{\mathrm{d}G_H(s)}{\mathrm{d}s} \le 1$; and

• $\lim \limits _{s \rightarrow \infty }{G_{H}(s)} = H(1 + c)$ with $0 < c \ll 1$.

Note that the dynamic feedback law $u^{*}$ is computed by (9) and (10) based only on the output measures $y_{i},i = 1,2,3$. The goal of the control is to utilize (10) as an “asymptotic robust proxy” of the ideal law (8) (see [44])¹.

As proven in [3], two assumptions must hold for $u^{*}$ to converge to the control law (8). Firstly, the matrix ${\varvec{b}}$ must represent a conservative guess of $b(\xi ,\eta )$ according to the following assumption:

Assumption 1

There exists a constant nonsingular matrix ${\varvec{b}} \in {\mathbb {R}}^{m \times m}$ and a number $0< \delta _{0} < 1$ such that

$$\begin{aligned} \max _{\varLambda \ \text {diagonal},\ \vert \varLambda \vert \le 1}{\vert \left[b(\xi ,\eta ) - {\varvec{b}} \right]\varLambda {\varvec{b}}^{- 1} \vert \le \delta _{0}},\ \forall (\xi ,\eta ). \end{aligned}$$

(11)

Equation (11) implies that $b_{\min } \le \vert b(\xi ,\eta ) \vert \le b_{\max }\$ for all $(\xi ,\eta )$ and for some pair $b_{\min } < b_{\max }$.

The second assumption concerns the zero-dynamics:

Assumption 2

The system ${\dot{\eta }} = z(\xi ,\eta )$, viewed as a system with input $\xi$ and state $\eta$, is input-to-state stable.

Under Assumptions 1 and 2, the main result in [3] is the following theorem.

Theorem 1

Considering system (7), with uncertain but bounded parameters, controlled by the output feedback law (9) and (10), there exists a choice of the design parameters such that, for any arbitrary compact set C, the equilibrium $(\eta ,\xi ,{\hat{\xi }},\sigma )=(0,0,0,0)$ is asymptotically stable, with a domain of attraction that contains C.

In particular, for every choice of C there are conditions for the choice of the parameters $\alpha _{i,1},\ \cdots ,\ \alpha _{i,3},\kappa ,K,L$:

• the parameters $\alpha _{i,1},\ \cdots ,\ \alpha _{i,3}$ to be chosen in such a way that the polynomial

  $$\begin{aligned} s^{3} + \alpha _{i,1}s^{2} + \alpha _{i,2}s + \alpha _{i,3} \end{aligned}$$

  is Hurwitz for $i = 1,\cdots ,3$, and it is shown in [3] that their values regulate the convergence speed of the error $e = \Vert \xi - {\hat{\xi }} \Vert$;

• the gain $\kappa$ bounds the value of $\Vert e \Vert$; if $\kappa$ is sufficiently high, the state trajectory of the controlled system enters, in finite time, an arbitrarily small compact system;

• as with the law (8), the matrix K in (10) has to be chosen such that $(A + BK)$ is Hurwitz;

• the role of the saturation level H of the function $G_{H}$ in (10) is to avoid that system (7) is affected by the destabilizing effect of peaking [45] and, hence, to avoid a finite escape time. The value of H depends only on the domain of attraction in which the initial conditions are taken.

4 Robust output-feedback control of a spacecraft system

This section details how the extended-observer paradigm can be used to address the spacecraft robust attitude control problem. Firstly, in Sect. 4.1, the normal form (3) for a spacecraft system is defined. Section 4.2 highlights the physical meaning of the assumptions needed for the robust control to work. Section 4.3 focuses on the disturbance rejection properties of the proposed control law.

4.1 Normal form of the spacecraft system

We now derive the normal form of (3). As customary in attitude studies, we assume $y = \left[q_{1},q_{2},q_{3} \right]^{\mathrm{T}}$ and set $u = L_{\tau }\tau$. For now, we also assume $\tau ^{\mathrm{ext}} = 0$ and, without loss of generality, we set $J = \mathrm{diag}\{ I_{x},I_{y},I_{z} \}$.

With the selected input-output, the vector of relative degree becomes $\{2,2,2\}$ [46], and the decoupling matrix

$$\begin{aligned} \varDelta (x) = \begin{bmatrix} \dfrac{q_{4}}{2I_{x}} &{} - \dfrac{q_{3}}{2I_{y}} &{} \dfrac{q_{2}}{2I_{z}} \\ \dfrac{q_{3}}{2I_{x}} &{} \dfrac{q_{4}}{2I_{y}} &{} - \dfrac{q_{1}}{2I_{z}} \\ - \dfrac{q_{2}}{2I_{x}} &{} \dfrac{q_{1}}{2I_{y}} &{} \dfrac{q_{4}}{2I_{z}} \\ \end{bmatrix} \end{aligned}$$

is nonsingular for $q_{4} \ne 0$.

Regarding the diffeomorphism T(x), recalling its structure from [41] and setting $\eta = q_{4}$, we can write

$$\begin{aligned} \begin{bmatrix} \xi \\ \eta \\ \end{bmatrix} = T(x) = \begin{bmatrix} q_{1} \\ L_{f}h_{1} \\ q_{2} \\ L_{f}h_{2} \\ q_{3} \\ L_{f}h_{3} \\ q_{4} \\ \end{bmatrix} = \begin{bmatrix} q_{1} \\ \dfrac{1}{2}( \omega _{x}q_{4} + \omega _{z}q_{2} - \omega _{y}q_{3} ) \\ q_{2} \\ \dfrac{1}{2}( \omega _{y}q_{4} - \omega _{z}q_{1} + \omega _{x}q_{3} ) \\ q_{3} \\ \dfrac{1}{2}( \omega _{z}q_{4} + \omega _{y}q_{1} - \omega _{x}q_{2} ) \\ q_{4} \\ \end{bmatrix}. \end{aligned}$$

This choice leads the system to the form (7), in which

$$\begin{aligned} \begin{aligned} a(\xi ,\eta ) =&\dfrac{1}{4}\omega \times ( \omega + q_{13} ) - \dfrac{1}{4}\omega ^{\mathrm{T}}q_{13}\omega \\&+ \dfrac{1}{2}( \left[q_{13} \times \right]+ q_{4}I_{3} )( J^{- 1}\omega ) \times (J\omega ) \end{aligned} \end{aligned}$$

(12)

and

$$\begin{aligned} b(\xi ,\eta ) = \dfrac{1}{2}( \left[q_{13} \times \right]+ q_{4}I_{3} )J^{- 1}. \end{aligned}$$

(13)

4.2 Extended-observer design for the spacecraft model

In the framework introduced so far, the condition (11) in Assumption 1 is at the basis of the definition of the extended observer and is of particular interest in spacecraft control, as it has a physical meaning that captures several criticalities that emerge in real spacecraft control applications.

Assumption 1 reduces to the existence and availability to the control of the nonsingular matrix ${\varvec{b}} \in {\mathbb {R}}^{m \times m}$, which represents the guess of $b(\xi ,\eta )$. In the considered case, even if it is trivial to show that $\vert b(\xi ,\eta ) \vert$ is bounded thanks to the unitary norm property of q, the identification of such matrix ${\varvec{b}}$ is not straightforward.

As the meaning behind Assumption 1 is to guarantee that the elements of $b(\xi ,\eta )u$ are bounded and have the correct sign [47], in this work we provide the controller with a dynamic estimation ${\hat{b}}(q)$ of the function$\ b(\xi ,\eta )$, as in [43], obtained from the available measures of q and from the nominal, or estimated, MOI ${\hat{J}}$. It is worth noting that the MOI of the satellite is time-varying and of nontrivial estimation, as it heavily depends on factors as the attitude of its auxiliary peripherals (e.g., solar panels, antennas, ...), the remaining propellant and its distribution in the tanks. For this reason, it is necessary to consider a difference between its nominal value ${\hat{J}}$ and the real one J.

Instead of Assumption 1, we will then verify the following one:

Assumption 3

There exists a function ${\hat{b}}(q):{\mathbb {R}}^{4}$ $\rightarrow {\mathbb {R}}^{r \times m}$ and a number $0< \delta _{0} < 1$ such that

$$\begin{aligned} \max _{\varLambda \ \text {diagonal}, \vert \varLambda \vert \le 1}\big \vert [b(\xi ,\eta ) - {\hat{b}}(q) ]\varLambda {{\hat{b}}(q)}^{- 1} \big \vert \le \delta _{0},\ \forall (\xi ,\eta ) \end{aligned}$$

(14)

with

$$\begin{aligned} {\hat{b}}(q) = \dfrac{1}{2}( [q_{13} \times ]+ q_{4}I_{3} ){{\hat{J}}}^{- 1}. \end{aligned}$$

(15)

The function ${\hat{b}}(q)$ of equation (15) represents the case in which the controller has what we may consider the “nominal value” of the high frequency gain.

Concerning Assumption 2, in view of Remark 1 and in line with Assumption 3 in [43] and with the concluding remarks in [3], it can be relaxed as follows.

Assumption 4

The system ${\dot{\eta }} = z(\xi ,\eta )$, viewed as a system with input $\xi$ and state $\eta$, is bounded-input-bounded-state stable.

The main result of the paper is then a consequence of Theorem 1.

Theorem 2

If the following condition holds:

$$\begin{aligned} \dfrac{\vert J^{- 1} - {{\hat{J}}}^{- 1} \vert \cdot \vert {\hat{J}} \vert }{\vert q_{4} \vert } < 1, \end{aligned}$$

(16)

where ${\hat{J}}$ is the estimated MOI tensor available to the controller, systems (7), (12) and (13), with uncertain but bounded parameters, controlled by the output-feedback law (9) and (10), asymptotically converges towards $(\xi ,{\hat{\xi }},\sigma )\ = \ (0,0,0)$, with an overall domain of attraction that contains an arbitrary compact set C.

Proof

The proof relies on the verification of Assumptions 3 and 4.

By substituting Eqs. (13) and (15) in Eq. (14) of Assumption 3, it becomes

$$\begin{aligned} \max _{\varLambda \ \text {diagonal},\vert \varLambda \vert \le 1}\vert \varTheta (q)( J^{- 1} - {{\hat{J}}}^{- 1} )\varLambda {\hat{J}}\ {\varTheta (q)}^{- 1} \vert \le \delta _{0}, \end{aligned}$$

(17)

in which we have set, for notation convenience, $\varTheta (q) = \left[q_{13} \times \right]+ q_{4}I_{3}$.

A conservative bound for the MOI estimation can be found by utilizing the submultiplicative property of the matrix norm, which, noting that $\vert \varTheta (q) \vert = 1$ and $\vert {\varTheta (q)}^{- 1} \vert = \dfrac{1}{\vert q_{4} \vert }$, yields

$$\begin{aligned} \vert \varTheta (q)( J^{- 1} - {{\hat{J}}}^{- 1} )\varLambda {\hat{J}}\ {\varTheta (q)}^{- 1} \vert \le \dfrac{\vert J^{- 1} - {{\hat{J}}}^{- 1} \vert \cdot \vert {\hat{J}} \vert }{\vert q_{4} \vert }, \end{aligned}$$

implying that, if the condition (16) holds, Assumption 3 is satisfied.

Under Assumption 3, the convergence proof replicates the one of the extended observer [3] (further detailed in [47]), with some awareness on ${\hat{b}}(q)$. In fact, the proof in [3] relies on the boundness of some quantities which depend on the guess ${\varvec{b}}$ used in the inequality (11). However, these quantities remain limited also when considering ${\hat{b}}(q)$ instead of ${\varvec{b}}$, i.e., inequality (14) instead of inequality (11), with ${\hat{b}}(q)$ defined as in (15), and the convergence proof still holds. Specifically, it is sufficient to retrace the proof in [3] noting that, as long as the state of the system is bounded,$\ \Vert {\hat{b}}(q) \Vert$,$\Vert [{\hat{b}}(q) ]^{- 1} \Vert$ and their time derivatives are bounded. In our case, $\Vert {\hat{b}}(q) \Vert = \dfrac{1}{2}\Vert {\hat{J}} \Vert$ is constant and, therefore, $\Vert \dfrac{\mathrm{d}{\hat{b}}(q)}{\mathrm{d}t} \Vert = 0$; $\Vert {\hat{b}}(q)^{- 1} \Vert$ is bounded by $\dfrac{\Vert {\hat{J}} \Vert }{\Vert q_{4}\ \Vert }$ which is bounded as long as $q_{4} \ne 0$; $\Vert \dfrac{\mathrm{d}( {\hat{b}}(q)^{- 1} )}{\mathrm{d}t} \Vert$ is bounded, as long as $q_{4} \ne 0$, since ${\dot{q}}$ is bounded due to the physical limitations of the spacecraft system.

As regards Assumption 4, we note that the zero dynamics of system (7) is not input-to-state stable (in the sense of Assumption 2) but, since $\eta = q_{4}$, it is bounded-input-bounded-state stable (in the sense of Assumption 3 of [43]), as $- 1{\le q}_{4} \le 1$ thanks to the unitary norm property of the quaternion representation.

Since Assumptions 3 and 4 are satisfied, the law (10) leads the components of $\xi$ to annihilate. The spacecraft attitude, consequently, converges to either of the two points $( \eta ,\xi ,{\hat{\xi }},\sigma ) = ( \pm 1,0,0,0)$, depending on its initial conditions. This completes the proof. $\square$

Remark 1

Noting that the two quaternions q and $- q$ represent the same attitude thanks to definition (1), it follows that a controller that stabilizes the chain of integrators in (7) leads the system to the correct attitude, independently of the convergence value of $\eta$. In other words, the convergence of the system to one of the two equilibrium points identified by Theorem 2 or to the other one depends on its initial conditions, but this does not impact the final attitude of the spacecraft.

Remark 2

Regarding the presence of $\dfrac{1}{\vert q_{4} \vert }$ in (16) we note that, as customary in singularity avoidance solutions for the so-called “large-scale manoeuvres” [46], we can divide any attitude regulation problem for which the initial value of $q_{4}$ is so close to the origin that (17) does not hold into multiple subsequent smaller rotations, in such a way that $\vert q_{4} \vert$ stays as close to 1 as desired.

Remark 3

The physical limitations of the system—the actuating capabilities of the reaction wheels mounted on spacecrafts are limited, typically, the torque is in the order of 0.1 Nm—set an upper-bound on the saturation level H of $G_{H}$ in the control law (10). In general, H depends on the considered set of possible initial conditions and on the matrix K that appears in (8) [3], but, since the mission can be divided in multiple arbitrarily small manoeuvres (see Remark 2), one can restrict such set accordingly. It is also worth remarking that, in the considered scenario, the components of $\tau$ are the ones that are directly subject to the actuator saturation, and, consequently, the components of the control law u are affected by the actuator saturation because of Eq. (5).

4.3 Fault tolerance and disturbance rejection

Due to the significant lifespan of spacecraft systems and to the difficult maintenance, rotating actuators such as reactions wheels are often subject to partial and total failures. Furthermore, during the launch phase, the structure of the satellite is under heavy stress and it is not unusual that it could be slightly deformed or one of its actuators damaged [9].

It is clear then that uncertainty is present not only in the estimation of J but also in the distribution matrix $L_{\tau }$, as any fault occurring to the reaction wheels or any frame modification impacts directly on the elements of $L_{\tau }$, as it will be further clarified in the following.

Faults causing the actuated torque to differ from the commanded control torque $\tau$ can be modelled by a multiplicative disturbance that affects the control torque. Let

$$\begin{aligned} F = {\mathrm{diag}}\{ f_{1},f_{2},\cdots ,f_{m} \},\ 0 \le f_{i} \le 1,\ i = 1,\cdots ,m \end{aligned}$$

be the matrix that collects the operative level of the actuators, where $f_{i} = 1$ means that the i-th actuator works perfectly, whereas $f_{i} = 0$ means that it is completely inoperative. The actuated torque $\tau '$ is then written as $\tau ' = F\tau$. Recalling Eq. (5), the torque $\tau$ computed by the controller is $\tau = {{\hat{L}}}_{\tau }^{\#}u$, where ${{\hat{L}}}_{\tau }^{\#}$ is the pseudo-inverse of the estimated, or nominal, distribution matrix ${{\hat{L}}}_{\tau }$. The actual control that drives the spacecraft is then

$$\begin{aligned} u' = L_{\tau }\tau ' = L_{\tau }F{{\hat{L}}}_{\tau }^{\#}u = L_{\tau }'{{\hat{L}}}_{\tau }^{\#}u, \end{aligned}$$

(18)

where $L_{\tau }' := L_{\tau }F$ represents the unknown actual distribution matrix of the spacecraft that includes also the effects of the deformations and faults. Note that such matrix can differ from the nominal one, ${{\hat{L}}}_{\tau }$, not only due to the presence of faults but also because of possible structural deformations that impact on the actuator axis projections on the rigid body axes.

By considering Eq. (18), the actual high-frequency gain takes into account the fact that the system is driven by the control $u'$ and not by the desired u:

$$\begin{aligned} b'(\xi ,\eta ) = \dfrac{1}{2}( \left[q_{13} \times \right]+ q_{4}I_{3} )J^{- 1}L_{\tau }'{{\hat{L}}}_{\tau }^{\#}. \end{aligned}$$

(19)

With the same reasoning of Theorem 2, it is possible to re-conduct the robustness property of the proposed controller to a bound on the quality of the estimation of both the matrices J and $L_{\tau }'$ available to the controller. As long as the controller is provided with a sufficiently good estimate ${\hat{b}}(q)$ of the high frequency gain, satisfying (14), its asymptotic properties are guaranteed, independently from the effect of the uncertainties on the other functions of $(\xi ,\eta )$ in (7).

In the analysis conducted so far, we assumed the absence of external torques, but this assumption may not be reasonable in real-world scenarios.

If we assume

$$\begin{aligned} \tau ^{\mathrm{ext}} = \left[\tau _{x}^{\mathrm{ext}},\tau _{y}^{\mathrm{ext}},\tau _{z}^{\mathrm{ext}} \right]^{\mathrm{T}} \ne 0, \end{aligned}$$

and let

$$\begin{aligned} w = \left[f_{1},f_{2},\cdots ,f_{n_{w}},\tau _{x}^{\mathrm{ext}},\tau _{y}^{\mathrm{ext}},\tau _{z}^{\mathrm{ext}} \right]^{\mathrm{T}}, \end{aligned}$$

we can rewrite system (7) as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{\eta }} = f(\eta ,\xi ), \\ {\dot{\xi }} = A\xi + B\left[q(\eta ,\xi ,w) + b(\eta ,\xi ,w)u \right], \\ y = C\xi \\ \end{array}\right. } \end{aligned}$$

(20)

with the matrices A, B, C defined as in the previous section.

In [43], it is shown that the proposed controller achieves, due to its integral action property, for a system in the form of (20), (i) complete rejection with respect to step disturbances and (ii) arbitrary attenuation of the effect of bounded disturbances with bounded derivatives. Both properties are very significant for practical applications. Concerning property (i), it is common to approximate a slow-varying disturbance $\tau ^{\mathrm{ext}}$ with a signal such that ${{\dot{\tau }}}^{\mathrm{ext}} = 0$, whereas property (ii) means that any disturbance that can be modelled as a series of sinusoidal components can be arbitrarily attenuated, and hence all the signals generated by an exosystem having eigenvalues on the imaginary axis, as customary in the internal model control paradigm, can be compensated arbitrarily by adjusting the parameters of the controller.

5 Simulations

This section reports several numerical simulations to validate the proposed control law.

We modelled a satellite with the same physical characteristics of the one considered in [40], with MOI matrix

$$\begin{aligned} J = \begin{bmatrix} 4.2 &{} 0 &{} 0 \\ 0 &{} 4.4 &{} 0 \\ 0 &{} 0 &{} 4.2 \\ \end{bmatrix}, \end{aligned}$$

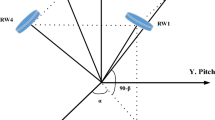
and with reaction wheels capable of providing torques in the range $[- 0.1;0.1]$ Nm. Regarding the reaction wheels configuration, we considered the rotated pyramid configuration considered in [48], shown in Fig. 1.

Fig. 1

Reaction wheels configuration

Recalling (4), it is immediate to characterize the nominal distribution matrix ${{\hat{L}}}_{\tau }$ as

$$\begin{aligned} {{\hat{L}}}_{\tau } = \left[ \begin{array}{c@{~~}c@{~~}c@{~~}c} \cos \beta _{1} \cos \theta _{1} &{} - \cos \beta _{2} \sin \theta _{2} &{} - \cos \beta _{3} \cos \theta _{3} &{} \cos \beta _{4} \sin \theta _{4} \\ \cos \beta _{1} \sin \theta _{1} &{} \cos \beta _{2} \cos \theta _{2} &{} - \cos \beta _{3} \sin \theta _{3} &{} - \cos \beta _{4} \cos \theta _{4} \\ \sin \beta _{1} &{} \sin \beta _{2} &{} \sin \beta _{3} &{} \sin \beta _{4} \\ \end{array}\right] . \end{aligned}$$

Setting $\theta _{i} = a\sin \frac{\sqrt{3}}{3}$ and $\beta _{i} = \frac{\pi }{4},i = 1,\cdots ,4$, (as in the pyramidal wheel configuration of Fig. 1) ${{\hat{L}}}_{\tau }$ becomes

$$\begin{aligned} {{\hat{L}}}_{\tau } = \dfrac{\sqrt{3}}{3}\begin{bmatrix} 1 &{} - 1 &{} - 1 &{} 1 \\ 1 &{} 1 &{} - 1 &{} - 1 \\ 1 &{} 1 &{} 1 &{} 1 \\ \end{bmatrix}. \end{aligned}$$

(21)

We consider the case in which an uncertain estimated MOI matrix ${\hat{J}}$ is available to the controller, with diagonal elements ranging in the interval $[2.9, 5.7]$, capturing estimation errors on J of $\pm 30\%$. As an example, to compute the guess of the high-frequency gain as in (11), in the presented simulations we set the estimated MOI matrix available to the controller as

$$\begin{aligned} {\hat{J}} = \begin{bmatrix} 4.6 &{} 0 &{} 0 \\ 0 &{} 4.8 &{} 0 \\ 0 &{} 0 &{} 4.6 \\ \end{bmatrix}, \end{aligned}$$

(22)

but similar simulation behaviour was observed with different choices of ${\hat{J}}$ within the allowed parameter range.

In all the simulations, condition (16) was always met.

Regarding the other parameters characterizing the extended observer and the controller we have set ${\{\alpha }_{i,1},\alpha _{i,2},\alpha _{i,3}\} = \left\{ 9,27,27 \right\} ,\ \forall i = 1,\cdots , 3$ and $\kappa = 100$. The last parameter, K, such was chosen so that the matrix $(A + BK)$ has its eigenvalues in $\left\{ - 0.25, - 0.5, - 0.25, - 0.5, - 0.25, - 0.5 \right\} .$

5.1 First simulation: nominal operation

The first simulation reports the system behaviour when no fault or disturbance is present. Figure 2 and 3 show the dynamics of the state $x = (q,\omega )$ and confirm that the control effectively stabilizes the system. Figure 2 shows that $q_{1}$, $q_{2}$ and $q_{3}$ annihilate with time in about 30 s, whereas $q_{4}$, representing the system zero-dynamics, remains bounded — it approaches 1 with time due to the norm condition. Figure 3 shows the angular velocities of the spacecraft over time, which also annihilates in about 30 s. In Fig. 4, which reports the control torques, we can see that the control input saturates during the first few seconds of the simulation, when the spacecraft has to correct its attitude significantly. The control becomes unsaturated as soon as it is reduced in magnitude due to the spacecraft approaching the target attitude.

For the sake of comparison, and to highlight the performance recovery of the proposed approach, we report in Figs. 5 and 6 the deviation observed between the states of a spacecraft controlled by (12)–(13) and one of a satellite governed by (8) with complete state feedback and provided with the correct estimation of the MOI matrix J. Figure 7 reports the deviation observed between the control torques of the two satellites, showing that the ideal control is recovered in a short amount of time.

Fig. 2

Spacecraft attitude over time, 1st simulation

Fig. 3

Spacecraft angular velocity over time, 1st simulation

Fig. 4

Control torques over time, 1st simulation

Fig. 5

Attitude deviation, 1st simulation

Fig. 6

Velocity deviation, 1st simulation

Fig. 7

Control torques deviation, 1st simulation

5.2 Second simulation: single fault

In the second simulation, we introduce a total failure on the fourth reaction wheel, leading to an actual distribution matrix

$$\begin{aligned} L_{\tau }' = \dfrac{\sqrt{3}}{3}\begin{bmatrix} 1 &{} - 1 &{} - 1 &{} 0 \\ 1 &{} 1 &{} - 1 &{} 0 \\ 1 &{} 1 &{} 1 &{} 0 \\ \end{bmatrix}, \end{aligned}$$

which affects the actual control action as in (18).

This uncertainty is captured by the modified high-frequency gain (19), but the controller is not aware of this event, as the guess ${\hat{b}}(q)$ is still given by (11) and (22), with the addition of (21). As it is highlighted in Fig. 8, the desired attitude is still reached after about 40 s, i.e., approximately 10 s later than in the former simulation.

Regarding the control torques, Fig. 9 shows that $\tau _{4}$ is always null (fault condition), while the other torques exhibit the same behaviour analysed in the first simulation: they saturate during the first part of the simulation and converge to zero as the attitude approaches the target one.

Fig. 8

Spacecraft attitude over time, 2nd simulation

Fig. 9

Control torques over time, 2nd simulation

5.3 Third simulation: multiple faults

For the third simulation, we report a case in which there is a generalized fault in all the actuators. In particular, the first and the second wheels actuate only $90\%$ and $50\%$ of the commanded torques, respectively, whereas the fourth wheel is inactive as in the previous simulation. For the third wheel, we modelled a deformation on its housing which causes its angle $\theta _{3}$ to be increased by $10{^\circ }$, while its angle $\beta _{3}$ is reduced by $5{^\circ }$. The resulting distribution matrix is

$$\begin{aligned} L_{\tau }' = \dfrac{\sqrt{3}}{3}\begin{bmatrix} 0.9 &{} - 0.5 &{} - 0.4954 &{} 0 \\ 0.9 &{} 0.5 &{} - 0.7075 &{} 0 \\ 0.9 &{} 0.5 &{} 0.5040 &{} 0 \\ \end{bmatrix}. \end{aligned}$$

Figures 10 and 11 show that the control still robustly stabilizes the system—even if, this time, about 50 s were necessary—despite having its controls compromised by the faults and despite both the MOI and the distribution matrices were wrongly estimated. Figure 11 also shows that, due to the actuator deformation, the torque $\tau _{1}$ saturates above the nominal lower saturation level $- 0.1$ Nm.

Fig. 10

Spacecraft attitude over time, 3rd simulation

Fig. 11

Control torques over time, 3rd simulation

For the sake of comparison, we now consider the controller proposed in [24], as it provides a robust solution against multiple faults without requiring any estimation of the MOI matrix and hence provides a fair comparison to our control logic, under similar assumptions. The same faults previously were applied to the satellite, with the tuneable controller parameters set according to [24]. From the analysis of Fig. 12 it is evident that, even if the controller is able to steer the spacecraft towards the desired attitude, the quaternion trajectory converges very differently from both the behaviours observed in Fig. 10 (our solution on the fault system) and Fig. 2 (that is the nominal case with no faults). The reason for this difference is to be found in the profile of the actuated controls, that is reported in Fig. 13. In fact, the controller in [24], as most of the existing robust approaches for attitude control, does not take into account the reconstruction of a nominal control law whereas the proposed control law asymptotically converges towards the control law employed in the first simulation, that was obtained following a pole-placement design. An equivalent behaviour is observed in Fig. 14, where the satellite system is governed by the sliding-mode control scheme proposed in [49] that, even neglecting the chattering-related shortcomings related to the sliding mode design, in turn assures the finite time convergence of the attitude tracking error under assumptions on the parameter uncertainty and the nature of the disturbances that are comparable to ours. The reconstruction of the nominal control law assured by our control logic allows for simpler mission planning and design phases, as the extended observer and the control law (13) lead the system towards trajectories closer to its ideal behaviour. We mention that, recent works such as [32, 50] and [51] focus mostly on data-driven/learning identification systems for faults and disturbances, showing noteworthy performances but, compared to works such as the present paper and [24], lacking asymptotic guarantees on their properties and requiring significant training phases with limited applicability to existing and orbiting spacecraft platform.

Fig. 12

Spacecraft attitude over time, benchmark for the 3rd simulation

Fig. 13

Control torques over time, benchmark for the 3rd simulation

Fig. 14

Spacecraft attitude over time, second benchmark for the 3rd simulation

5.4 Fourth simulation: external disturbances

In the fourth simulation, we consider the system in presence of disturbances. All the spacecraft actuators are fully functional and the system is subject to an additional constant disturbance torque, whose components, over the principal axes of inertia of the spacecraft, are $\tau ^{\mathrm{ext}} = [- 0.06, \ 0.05, \ 0.08]^{\mathrm{T}}$ Nm, as shown in Fig. 15. Even in the presence of these disturbances, which are comparable in magnitude to the control itself (recall that the torque saturation level is 0.1 Nm), Fig. 16 shows that the control law (13) still stabilizes the system.

It is interesting to note how the controls successfully reconstruct and compensate the disturbances of Fig. 15. The controls are shown in Fig. 17, and their projections on the principal axes of inertia (computed by using the distribution matrix) are shown in Fig. 18: the steady-state values are such that the constant disturbances are exactly cancelled.

Fig. 15

Disturbance torques over time, 4th simulation

Fig. 16

Spacecraft attitude over time, 4th simulation

Fig. 17

Control torques over time, 4th simulation

Fig. 18

Resulting control torques over time, 4th simulation

5.5 Fifth simulation: sinusoidal disturbances

The fifth and final simulation reports, in the same fault-free case of the previous simulation, the case in which the disturbances have a time-varying component. As depicted in Fig. 19, the disturbance torques are biased sinusoidal signals at different frequencies:

$$\begin{aligned} \tau ^{\mathrm{ext}} = \begin{bmatrix} 0.01\sin \,t - 0.05 \\ {0.05\sin }(2t) + 0.01 \\ 0.01\sin (3t) \\ \end{bmatrix}\text {Nm}. \end{aligned}$$

Figure 20 shows that, practically, the control law (13) still manages to stabilize the system by using, this time, sinusoidal control torques—see Fig. 21. However, by analysing the torque projections on the principal axes of inertia, depicted in Fig. 22, we may notice that there is not a perfect reconstruction of the external torque of Fig. 19, as expected (see Section 4.3). This small error, which is in the order of $10^{- 4}$ Nm, results in small oscillations of the attitude, in the order of $10^{- 5}$, as shown in Fig. 23.

Fig. 19

Disturbance torques over time, 5th simulation

Fig. 20

Spacecraft attitude over time, 5th simulation

Fig. 21

Control torques over time, 5th simulation

Fig. 22

Resulting Control torques over time, 5th simulation

Fig. 23

Spacecraft attitude oscillations, 5th simulation

6 Conclusions and future work

This paper presented a control strategy for the attitude control of a spacecraft, robust to unknown, but bounded, uncertainties in the system parameters and external disturbances. The main contribution is the adoption of the extended-observer paradigm of [3, 43] in the attitude control problem. The resulting control law is then robust also to uncertainties in the high-frequency gain matrix and, as shown in the paper, this property allows us to include uncertainties that are not commonly addressed by other robust control methods, such as uncertainties in the actuators positioning and faults. As shown also by simulation results, the control is in fact robust, within the physical limits (e.g., a suitable number of actuators must be available, at least partially, as required by a rank condition on the distribution matrix) in terms of total faults, partial faults and deformations of the actuators. The controller is also able to achieve zero steady-state error for step disturbances and an arbitrarily small error for sinusoidal ones.

Future work is aimed at extending the developed framework to the problems of attitude tracking and constellation control, as well as its application to flexible satellites.