Abstract
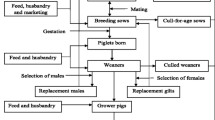
This paper presents a formulation and resolution of a two-stage stochastic linear programming model with recourse for sow farms producing piglets. The proposed model considers a medium-term planning horizon and specifically allows optimal replacement and schedule of purchases to be obtained for the first stage. This model takes into account sow herd dynamics, housing facilities, reproduction management, herd size with initial and final inventory of sows and uncertain parameters such as litter size, mortality and fertility rates. These last parameters are explicitly incorporated via a finite set of scenarios. The proposed model is solved by using the algebraic modelling software OPL Studio from ILOG, in combination with the solver CPLEX to solve the linear models resulting from different instances considered. The article also presents results obtained with previous deterministic models assessing the suitability of the stochastic approach. Finally, the conclusions drawn from the study including an outlook are presented.
Similar content being viewed by others
References
Albornoz VM, Canales C (2006) Total allowable catch for managing squat lobster fishery using stochastic nonlinear programming. Comput Oper Res 33:2113–2124
Albornoz VM, Contesse L (1999) Modelos de Optimización Robusta un Problema de Planificación Agregada de la Producción bajo Incertidumbre en las Demandas. Invest Oper 7(3):1–15
Alonso-Ayuso A, Escudero L, Ortuño MT (2005) Modelling production planning and scheduling under uncertainty. In: Wallace SW, Ziemba WT (eds) Applications of stochastic programming. SIAM, Philadelphia
Beale EML (1955) On minimizing a convex function subject to linear inequalities. J R Stat Soc, Ser B 17:173–184
Birge JR, Louveaux FV (1997) Introduction to stochastic programming. Springer, New York
Dantzig GB (1955) Linear programming under uncertainty. Manag Sci 1:197–206
Escudero L, Kamesan P, King A, Wets R (1993) Production planning via scenarios modelling. Ann Oper Res 43:311–335
Gupta A, Maranas CD (2003) Managing demand uncertainty in supply chain planning. Comput Chem Eng 27:1219–1227
Huirne RB, Dijkhuizen AA, Van Beek P, Hendriks THB (1993) Stochastic dynamic programming to support sow replacement decisions. Eur J Oper Res 67:161–171
Jalvingh AW, Dijkhuizen AA, van Arendonk JAM (1992) Dynamic probabilistic modelling of reproduction and management in sow herds. General aspects and model description. Agric Syst 39:133–152
Kingwell R (1996) Programming models of farm supply response: the impact of specification errors. Agric Syst 50:307–324
Kristensen AR (1988) Hierarchic Markov processes and their applications in replacement models. Eur J Oper Res 35:207–215
Kristensen AR (1993) Markov decision techniques applied to the animal replacement problem. DrSc dissertation, Dina KVL Dep of Animal Science and Animal Helth, The Royal Veterinary and Agricultural University, Copenhagen, Denmark
Mula J, Poler R, García-Sabater JP, Lario FC (2006) Models for production planning under uncertainty: A review. Int J Prod Econ 103:271–285
Plà LM (2007) Review of mathematical models for sow herd management. Livest Sci 106:107–119
Plà LM, Faulin J, Rodríguez S (2008) A linear programming formulation of a semi-Markov model to design pig facilities. J Oper Res Soc Advance online publication 16 April 2008; doi:10.1057/palgrave.jors.2602599
Rodríguez SV, Albornoz VM, Plà LM (2008) A mixed-integer linear programming model for scheduling replacements and purchases in sow farms. Technical report, Mathematic Department, University of Lleida
Rowland WW, Langemeier MR, Schurle BW, Featherstone AM (1998) A nonparametric efficiency analysis for a sample of Kansas swine operations. J Agric Appl Econ 30:189–199
Ruszczynski A, Shapiro A (eds) (2003) Stochastic programming. Handbook in operations research and management science, vol 10. North-Holland, Amsterdam
Wallace SW, Ziemba WT (eds) (2005) Applications of stochastic programming. SIAM, Philadelphia
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rodríguez, S.V., Albornoz, V.M. & Plà, L.M. A two-stage stochastic programming model for scheduling replacements in sow farms. TOP 17, 171–189 (2009). https://doi.org/10.1007/s11750-009-0087-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11750-009-0087-2