Abstract
This paper presents new specification tests for a general synchronous additive concurrent model formulation. As a novelty, our proposal does not require a preliminary model or error structure estimation. No tuning parameters are involved either. We develop a suitable test statistic using the martingale difference divergence coefficient. As a result, this statistic measures the departure from the conditional mean independence in the concurrent model framework, considering the information of all observed time instants. In particular, global as well as partial dependence tests are introduced. Then, we allow one to quantify the effect of a group of covariates or to apply covariates selection one by one. We obtain its asymptotic distribution under the null and propose a bootstrap algorithm to compute the p-values in practice. Through simulations, we illustrate our method, and its performance is compared to existing competitors. In addition, we use this in the analysis of three real datasets related to gait data, flu activity, and casual bike rentals.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A general concurrent model is a regression model where the response \(Y=(Y_1,\dots , Y_q)\in \mathbb {R}^q\), for \(q\ge 1\), and \(p\ge 1\) covariates \(X=(X_1,\dots , X_p)\in \mathbb {R}^p\) are all functions of the same argument \(t\in \mathcal {D}\), and the influence is concurrent, simultaneous or point-wise in the sense that X is assumed to only influence Y(t) through its value \(X(t)=\left( X_1(t),\dots ,X_p(t) \right) \in \mathbb {R}^p\) at time t by the relation
where \(m(\cdot )\) is an unknown function collecting the \(\mathbb {E}\left[ Y(t)\arrowvert _{X(t)} \right] \) information and \(\varepsilon (t)\) is the error of the model. This last is a process which is assumed to have mean zero, independent of X and with covariance function \(\Omega (s,t)=\mathbb {C}\left[ \varepsilon (s),\varepsilon (t)\right] \), being \(\mathbb {C}[\cdot ,\cdot ]\) the covariance operator.
The concurrent model displayed in (1) is in the middle of longitudinal and functional data. This classification depends on the number of observed time instants in the t domain \(\mathcal {D}\). When this number is dense enough, the sample data can be treated as curves, translating into a functional data framework. Otherwise, if time instants are spaced respective to the t domain and not dense, a longitudinal framework will be more suitable. Determining the inflection point between both situations is still an open problem. For a discussion on this topic, we refer the reader to the work of Wang et al. (2017).
There are plenty of contexts where the (1) formulation arises both in functional or longitudinal framework form. The functional concurrent model can be employed in any situation where data can be monitored, like in health, environmental or financial issues among others. Some examples can be seen in works such as the ones of Xue and Zhu (2007) or Jiang and Wang (2011) for the longitudinal data context. They perform epidemiology studies of AIDS datasets. Other real data examples in medicine can be found in Goldsmith and Schwartz (2017) or Wang et al. (2017). Goldsmith and Schwartz (2017) perform a blood pressure study to detect masked hypertension. For their part, authors in Wang et al. (2017) use the concurrent model in a data study of flu prevalence in the USA. Furthermore, they model Alzheimer’s disease progression using brain neuroimaging data. More examples of health and nutrition are displayed in Kim et al. (2018) and Ghosal and Maity (2022a). They perform studies related to gait deficiency, dietary calcium absorption, and the relation between child mortality and financial power in different countries. Examples in the environmental field are collected in works such as Zhang et al. (2011) or Ospína-Galindez et al. (2019). These studies are based on describing forest nitrogen cycling and modeling the rainfall ground, respectively. A completely different example is the work of Ghosal and Maity (2022b), where casual bike rentals in Washington, D.C., are concurrently explained using meteorological variables. This extensive list of examples reveals that the concurrent model is a very transversal and wide-employed tool nowadays.
An inconvenience of the concurrent model general formulation, displayed in (1), is that the \(m(\cdot )\) structure is quite difficult to be estimated in practice. For this reason, it is common to consider some assumptions about its form. In the literature, it is quite common to assume linearity, which translates into taking \(m(t,X(t))=\beta (t)X(t)\) in (1), and work under this premise. However, this assumption can be quite restrictive in practice. Thus, more general structures are needed to model real examples properly. This last results in a gain in flexibility but adds complexity to the estimation process. Maity (2017) discusses the effort made for estimating different concurrent model structures. This paper highlights that more information is needed to correctly estimate the function \(m(\cdot )\). In conclusion, it is crucial to guarantee that there exists useful information on the covariates X to model the behavior of Y as a preliminary step. Therefore, covariates selection algorithms for the concurrent model are of interest to avoid irrelevant covariates and simplify the estimation process.
As a result, the first step to assure the veracity of the model structure displayed in (1) is to verify if all p covariates \(\{X_1(t),\dots , X_p(t)\}\) contribute to the correct explanation of Y(t), or some can be excluded from the model formulation. For this purpose, taking \(D\subseteq \{1,\dots ,p\}\), a dependence test can be performed by means of testing
where \(X_D(t)\) denotes the subset of X(t) considering only the covariates with index in D, \(\mathcal {D} \setminus \mathcal {N}\) is the domain of t minus a null set \(\mathcal {N} \subset \mathcal {D}\) and \(\mathcal {V} \subset \mathcal {D}\) is a positive measure set.
Quoting Zhang et al. (2018), the above problem is very challenging in practice without assuming any structure of \(m(\cdot )\). This drawback is due to the vast class of alternatives targeted, related to growing dimension and nonlinear dependence. To solve this inconvenience, the authors propose testing the nullity of the main effects first, keeping a type of hierarchical order. Then, it is tested if additive and separate effects first enter the model before considering interactive structures. This results in the new test displayed in (2).
Then, rejection of the null hypothesis of (2) automatically implies the rejection of the \(H_0: \mathbb {E} \left[ Y(t) \arrowvert _{X_D(t)} \right] =\mathbb {E}\left[ Y(t) \right] \) hypothesis. It is important to highlight that the reciprocal is not always true. In this way, the model (1) only makes sense if it is possible to reject the \(H_0\) hypothesis of (2). Otherwise, the covariates do not supply relevant information to explain Y. It is notorious that formulation (2) collects a wide range of dependence structures between X and Y in terms of additive regression models, where \(m\left( t,X(t) \right) =F_1\left( t,X_1(t) \right) +\dots +F_p\left( t,X_p(t) \right) \). Moreover, it is no need to know the real form of \(m(\cdot )\) to determine whether the effect of X is significant.
To the best of our knowledge, there is no literature on significance tests for the additive concurrent model that avoids previous model estimation or extra tuning parameters. We refer to Wang et al. (2017) and Ghosal and Maity (2022a) for these in the linear formulation. They both propose effect tests over the \(\beta (t)\) function making use of the empirical likelihood. Thus, once the model parameters are estimated in the linear framework, the authors provide tools to test if all p covariates are relevant or, on the contrary, if some can be excluded from the model. Nevertheless, a suitable effects estimation involves several tuning parameters and the linearity hypothesis. These are necessary to guarantee the adequate performance of the cited procedures. In terms of the \(\beta (t)\) structure estimation, different approaches arise. For example, Wang et al. (2017) propose using a local linear estimator, which depends on a proper bandwidth selection. In contrast, Ghosal and Maity (2022a) employs an expansion into a finite number of elements of a functional basis. This expansion requires the number of considered terms selection. In addition, this last procedure needs to estimate the error model structure. This process translates into an additional functional basis representation and estimation of extra parameters. All this translates into difficulties in the estimation process, even if the linear hypothesis can be accepted. Currently, Kim et al. (2018) developed a new significance test in a more general framework to alleviate the linear hypothesis assumption: additive effects are considered in (1). This work employs F-test techniques over a functional basis representation of the additive effects to detect relevant covariates. Again, this technique depends on an adequate preliminary estimation of the model effects to be able to select relevant covariates by applying significance tests. However, the correct selection of the number of basis functions for each considered covariate/effect representation is still an open problem. These quantities play the role of tuning parameters. Furthermore, a proper error variance estimation is needed to standardize the covariates as an initial step. As this structure is unknown in practice, Kim et al. (2018) assumes that this can be decomposed as a sum of two terms. The first one is a zero-mean smooth stochastic process, and the second term is a zero-mean white noise measurement error with variance \(\sigma ^2\), resulting in the autocovariance function \(\Omega (s,t)=\Sigma (s,t)+\sigma ^2 \mathbb {I}\{s=t\}\). Nevertheless, this assumption can be restrictive in practice. In consequence, significance tests without any assumption in the model structure and no necessity of a preliminary estimation step are desirable.
Other procedures for covariates selection with a different methodology are the Bayesian selectors and the penalization techniques used in the concurrent model estimation process. We can highlight the works of Goldsmith and Schwartz (2017) or Ghosal et al. (2020) in the linear formulation and the one of Ghosal and Maity (2022b) for general additive effects. While Goldsmith and Schwartz (2017) uses the spike-and-slab regression covariates selection procedure, Ghosal et al. (2020) and Goldsmith and Schwartz (2017) implement penalizations based on LASSO (Tibshirani 1996), SCAD (Fan and Li 2001), MCP (Zhang 2010) or its grouped versions (Yuan and Lin 2006), respectively. As a result, the selection of covariates is implemented together with estimation. Nevertheless, some tuning parameters are needed in all these methodologies: it is necessary to determine the number of basis functions to represent the effects in all of them, jointly with prior parameters, in case of the spike-and-slab regression, or the amount of penalization otherwise. As a result, the estimation of tuning parameters applies in these approaches as well.
In this paper, we deal with this concern by bridging a gap for significance tests without previous model estimation. The new proposal for specification testing can assess the usefulness of a vector X for modeling the expectation of the Y vector in a pretty general formulation. Besides, this approach avoids extra tuning parameters estimation, as well as the need to model the error structure. For this aim, we propose a novel statistic for the concurrent model based on the martingale difference divergence ideas of Shao and Zhang (2014) to perform (2). As a result, this approach tests the effect of the covariates in the explanation of Y no matter the underlying form of \(m(\cdot )\) while assuming additive effects.
It is important to notice that one can consider \(D=\{1,\dots ,p\}\) to perform (2), which translates in testing if all p covariates are relevant, or only a subset \(D\subset \{1,\dots ,p\}\) with cardinality \(1\le d<p\). In this last case, one tests if only a bunch of covariates are relevant, excluding the rest from the model. A special case is to consider \(D=\{j\}\) for some \(j=1,\dots ,p\). This approach allows to implement covariates screening with no need to estimate the regressor function. Thus, it is possible to test the effect of every covariate. This results in \(j=1,\dots ,p\) partial tests of the form
Thus, one can test if a small subset of \(\{1,\dots ,p\}\) is suitable to fit the model or if all covariates need to be considered. As a result, it is possible to avoid noisy covariates entering the model and reduce the problem dimension.
The rest of the paper is organized as follows. In Sect. 2, the martingale difference divergence coefficient is introduced along with some remarkable properties. We present the new specification tests in Sect. 3. A theoretical justification for their proper behavior is given and a bootstrap scheme is proposed to calibrate these in practice. A simulation study to test their performance is carried out in Sect. 4, jointly with a comparison involving Ghosal and Maity (2022a) and Kim et al. (2018) competitors. Next, the proposed tests are applied to three real datasets in Sect. 5. Eventually, some discussion arises in Sect. 6.
2 Martingale difference divergence (MDD)
The martingale difference divergence (MDD) was introduced by Shao and Zhang (2014). This coefficient is a natural extension of the distance covariance (Székely et al. 2007; Szekely and Rizzo 2017). The MDD measures the departure from conditional mean independence between a vector response variable \(Y\in \mathbb {R}^q\) and a vector predictor \(X\in \mathbb {R}^p\). This coefficient was introduced in Shao and Zhang (2014) for the scalar response case, taking \(q=1\), and was later generalized in Park et al. (2015) for values of \(q\ge 1\). Hence, this idea can be used to screen out numerical variables that do not contribute to the conditional mean explanation of Y. This translates into the test
Therefore, a coefficient measuring the difference between the conditional mean and the unconditional one is needed to perform (4). For this aim, following similar ideas and argumentation of the distance covariance measure of Székely et al. (2007), it emerges the MDD coefficient.
Then, for \(Y\in \mathbb {R}^q\) and \(X\in \mathbb {R}^p\), the MDD of Y given X is the nonnegative number \(MDD(Y\arrowvert _X)\) defined by
where \(c_p=\pi ^{(1+p)/2}/ \Gamma ((1+p)/2)\), being \(\Gamma (\cdot )\) the gamma function, \(\psi _{Y,X}(s)=\mathbb {E}[Y e^{i<s,X>}]\), \(\psi _Y=\mathbb {E}[Y]\) and \(\psi _X(s)=\mathbb {E}[ e^{i<s,X>}]\). \(i=\sqrt{-1}\) is the imaginary unit, \(<\cdot ,\cdot>\) the inner product, \(\arrowvert z \arrowvert _q=\sqrt{z^Hz}\) the complex norm of \(z\in \mathbb {C}^q\), where \(z^H\) denotes the conjugate transpose and \(\Vert \cdot \Vert _p\) is the Euclidean norm of the \(\mathbb {R}^p\) space.
It can be seen in Theorem 1 of Shao and Zhang (2014) and Proposition 3.1 of Park et al. (2015) that, if it is verified \(\mathbb {E}[\Vert Y\Vert _q^2] + \mathbb {E}[\Vert X\Vert _p^2]<\infty \) and \(\mathbb {E}[\Vert Y\Vert _q^3] + \mathbb {E}[\Vert X\Vert _p^3]<\infty \) respectively, and being \((X',Y')\) and \((X'',Y'')\) independent copies of (X, Y), an alternative way to the definition (5) is
where \(L(y,y')=\Vert y-y' \Vert _q^2/2\) and \(J(x,x')=\Vert x-x'\Vert _p\).
A proof for first expression of Eq. (6), considering \(q=1\), follows from Theorem 1 of Shao and Zhang (2014). Similar arguments can be employed for general \(q\ge 1\) considering the q-norm instead. The second formulation results from expanding and canceling terms. Some guidelines can be found in the proof of Theorem 1 of Shao and Zhang (2014) as well.
Since, in general, \(MDD(Y\arrowvert _X)\not =MDD(X\arrowvert _Y)\), this is named divergence instead of distance. The MDD equals 0 if and only if it is verified the \(H_0\) hypothesis of (4) and otherwise \(MDD>0\). Therefore, the test (4) can be rewritten as the new one displayed in (7).
Next, an unbiased estimator of MDD introduced in Zhang et al. (2018) is presented. Then, given n independent observations \((\mathbf {X_n},\mathbf {Y_n})=\{ (X_i,Y_i), i=1,\dots ,n \}\) from the joint distribution of (X, Y), with \(X_i=(X_{i1},\dots ,X_{ip})^\top \in \mathbb {R}^p\) and \(Y_i=(Y_{i1},\dots ,Y_{iq})^\top \in \mathbb {R}^q\), it is possible to define \(A=(A_{il})_{i,l=1}^n\) and \(B=(B_{il})_{i,l=1}^n\), where \(A_{il}=\Vert X_i-X_l\Vert _p\) and \(B_{il}=\Vert Y_i-Y_l\Vert _q ^2/2\) for \(i,l=1,\dots ,n\). Following the \(\mathcal {U}\)-centered ideas of Park et al. (2015), the \(\mathcal {U}\)-centered versions of A and B can be defined, \(\overline{A}\) and \(\overline{B}\) respectively, given by
As a result, an unbiased estimator for MDD is defined as
A proof that \(MDD_n^2(\mathbf {Y_n}\arrowvert _\mathbf {X_n})\) is an unbiased estimator for \(MDD^2(Y\arrowvert _X)\) can be found in Section 1.1 of the supplementary material of Zhang et al. (2018) for the \(q=1\) case. An extension for the case considering \(q\ge 1\) is displayed in the proof of Proposition 3.4 given in Park et al. (2015).
An important characteristic of the \(MDD_n^2(\mathbf {Y_n}\arrowvert _\mathbf {X_n})\) unbiased estimator defined in (8) is that this is a \(\mathcal {U}\)-statistic of order four. In fact, with some calculation, it can be proved that
with symmetric kernel function
where \(Z_i=(X_i,Y_i)\) for \(i=1,\dots ,n\) and the summation is over all permutation of the 4-tuples of indices (i, k, l, r).
A justification for this selection of kernel function can be found in Section 1.1 of the supplementary material of Zhang et al. (2018). There, it is also proved the unbiasedness of the MDD estimator displayed in (8) for the \(q=1\) case. It is straightforward to generalize these results to \(q\ge 1\) just considering the \(\mathbb {R}^q\) metric in the \(B_{il}\) definition. Then, the \(\phi (\cdot )\) kernel is obtained again.
Then, given the (9) formulation with kernel \(\phi (\cdot )\), one can directly notice that \(MDD_n^2(\mathbf {Y_n}\arrowvert _\mathbf {X_n})\) is a \(\mathcal {U}\)-statistic of order four by proper definition (see for example Lee (1990)). Then, theoretical results of \(\mathcal {U}\)-statistics can be employed to obtain its asymptotic distribution and to perform the specification test displayed in (4). Specifically, an example of this last is collected in Theorem 2.1 for the \(q=1\) case in Zhang et al. (2018). Next, this property is used in the next section to derive the asymptotic distribution of new statistics devoted to testing specification in the concurrent model.
3 Significance tests based on MDD
Once we have a tool to measure conditional mean independence between \(Y=(Y_1,\dots ,Y_q)^\top \in \mathbb {R}^q\) and a vector \(X=(X_1,\dots ,X_p)^\top \in \mathbb {R}^p\), this approach is adapted to the concurrent model case. For this aim, we use the ideas presented in the work of Zhang et al. (2018) for the vectorial framework.
Henceforth, we assume a situation where all points of the curves are observed synchronously. However, the preliminary assumption that all trajectories are fully observed can be quite restrictive in practice. Section 3.2 it is showed how to adapt this requirement to contexts where some points are missed, adjusting the procedure to more realistic situations. Thus, a total of \(\{t_u\}_{u=1}^{\mathcal {T}}\in \mathcal {D}\) time instants are considered and there are \(n_u\) observed samples, each of them of the form \(\{ Y_{i_u}(t_u),X_{i_u}(t_u) \}_{i_u=1}^{n_u}\). As mentioned before, assuming all curves observed at the same time instants translates into \(n_u=n\) for all \(u=1,\dots ,\mathcal {T}\). Then, we have a sample of the form \(\left( \mathbf {Y_n(t)},\mathbf {X_n(t)} \right) =\{\left( Y_{i}(t_u),X_{i}(t_u)\right) , \; u=1,\dots ,\mathcal {T}\}_{i=1}^{n}\). A graphic example of our current situation considering \(q=1\) and \(p=2\) covariates for a concurrent model with a structure similar to (1) is displayed in Fig. 1.
In this way, we want to include all the information provided by the observed time instants \(\{t_u\}_{u=1}^{\mathcal {T}}\in \mathcal {D}\) in a new statistic. Besides, as mentioned above, we can be interested in testing dependence not only considering all covariates but a subset \(D\subset \{1,\dots ,p\}\). As a result, an integrated dependence test is applied over the complete trajectory, considering the information provided by D. Rewriting (2), this gives place to the test
In order to implement the new test introduced in (10) a proper estimator of \(\int _{\mathcal {D}} MDD^2(Y(t)\arrowvert _{X_j(t)}) dt\) for every \(j\in D\) is needed. For this purpose, we propose an integrated statistic based on
being \(\widetilde{MDD}_{n}^2(\mathbf {Y_n(t)}\arrowvert _{\mathbf {X_{nj}(t)}})= \int _{\mathcal {D}} MDD_{n}^2(\mathbf {Y_n(t)}\arrowvert _{\mathbf {X_{nj}(t)}})dt\) and
a suitable variance estimator of \(\sum _{j\in D} \widetilde{MDD}_{n}^2(\mathbf {Y_n(t)}\arrowvert _{\textbf{X}_{nj}}(t))\) with \(c_n\)
See Sect. 3.1 for in-depth details about \(\widehat{\widetilde{\mathcal {S}}}_D^2\) calculation.
The integrated version \(\widetilde{MDD}_{n}^2(\mathbf {Y_n(t)}\arrowvert _{\mathbf {X_{nj}(t)}})\) remains a \(\mathcal {U}\)-statistic of order four. This is because, denoting by \(Z_{ij}(t)=\left( X_{ij}(t), Y_i(t) \right) \) and \( ( \widetilde{A_{sw}B_{uv}} )_j=\int _{\mathcal {D}} \left( A_{sw}(t) \right) _j \left( B_{uv}(t)\right) _j dt\) for all (s, w, u, v), we have that \(\widetilde{\phi (Z_{ij}(t),Z_{kj}(t),Z_{lj}(t),Z_{rj}(t))}\) equals to
and this remains a measurable and symmetric function. Then, similar to (9) argumentation, it is easy to see that it is possible to write
which keeps the structure of a \(\mathcal {U}\)-statistic of order 4. It can be proved that \(\widetilde{MDD}_n^2(\mathbf {Y_n(t)}\arrowvert _{\mathbf {X_{nj}(t)}})\) is an unbiased estimator of \(\widetilde{MDD}^2(Y(t)\arrowvert _{X_j(t)})\). See Section 1 of the Online Supplementary Material.
Theorem 1
Under the assumption of \(H_0\) and verifying
for \(\mathbb {V}[\cdot ]\) the variance operator and \(\text {dcov}(\cdot ,\cdot )\) the distance covariance, it is guarantee that \(T_{D} \longrightarrow ^d N(0,1)\) when \(n\longrightarrow \infty \) and \(\widehat{\widetilde{\mathcal {S}}}_D^2/\widetilde{\mathcal {S}}_D^2\longrightarrow ^p 1\).
Theorem 1 guarantees the asymptotic convergence of the \(T_D\) statistic displayed in (11) to a normal distribution under some assumptions. Proof of this result is collected in Section 3 of the Supplementary Material, which makes use of the Hoeffding decomposition for \(\mathcal {U}\)-statistics carried out in Section 2 of the same document.
One drawback is that the asymptotic convergence of the \(T_D\) statistic can be very slow in practice. To solve this issue we approximate the p-value using a wild bootstrap scheme. Its scheme is collected in Algorithm 2. The proof of the consistency related to the proposed wild bootstrap procedure and that of the variance estimator for the concurrent model case is omitted due to extension. However, the proof results from plugging the integrated version in that of Zhang et al. (2018), introduced in Section 1.6 of their supplementary material.
Algorithm 2
(Wild bootstrap scheme for global dependence test using MDD)
-
1.
For \(u=1\dots ,\mathcal {T}\):
-
1.1.
Calculate
$$\begin{aligned} (T_{u})_D=\sqrt{\left( {\begin{array}{c}n\\ 2\end{array}}\right) }\sum _{j\in D} MDD_{n}^2(Y(t_u)\arrowvert _{X_j(t_u)}). \end{aligned}$$ -
1.2.
Obtain
$$\begin{aligned} (\hat{\mathcal {S}}_{u})_D= \sqrt{\frac{2}{n(n-1)c_n}\sum _{1\le k<l\le n} \sum _{j,j'\in D}\left( \overline{A}_{kl} (t_u)\right) _j \left( \overline{A}_{kl} (t_u)\right) _{j'} \overline{B}^2_{kl}(t_u)}, \end{aligned}$$where \(\left( \overline{A}_{kl} (t_u)\right) _j\) and \(\overline{B}_{kl}(t_u)\) are the \(\mathcal {U}\)-centered versions of \(\left( A_{kl}(t_u) \right) _j=\arrowvert X_{kj}(t_u)-X_{lj}(t_u)\arrowvert \) and \(B_{kl}(t_u)=\Vert Y_k(t_u)-Y_l(t_u)\Vert _q^2/2\), respectively.
-
1.3.
Generate the sample \(\{e_{i}\}_{i=1}^{n}\), where \(e_{i}\) are i.i.d. N(0,1).
-
1.4.
Define the bootstrap \(MDD^{*2}_{n}(Y(t_u)\arrowvert _{X_j(t_u)})\) version as
$$\begin{aligned} MDD^{*2}_{n}(Y(t_u)\arrowvert _{X_j(t_u)})=\frac{1}{n(n-1)} \sum _{k\ne l} \left( \overline{A}_{kl} (t_u)\right) _j \overline{B}_{kl}(t_u) e_k e_l \end{aligned}$$ -
1.5.
Obtain the bootstrap statistic numerator
$$\begin{aligned} (T_{u}^*)_D=\sqrt{\left( {\begin{array}{c}n\\ 2\end{array}}\right) } \sum _{j\in D} MDD_{n}^{*2}(Y(t_u)\arrowvert _{X_j(t_u)}). \end{aligned}$$ -
1.6.
Calculate the bootstrap variance estimator
$$\begin{aligned} (\hat{\mathcal {S}}^{*}_{u})_D= \sqrt{\frac{1}{\left( {\begin{array}{c}n\\ 2\end{array}}\right) } \sum _{1\le k<l\le n} \sum _{j, j' \in D} \left( \overline{A}_{kl} (t_u)\right) _j \left( \overline{A}_{kl} (t_u)\right) _{j'} \overline{B}^2_{kl}(t_u) e^2_k e^2_l}. \end{aligned}$$ -
1.7.
Repeat steps 1.3\(-\)1.6 a number B of times obtaining the sets \(\{(T^*_{u})_D^{(1)},\dots , (T^*_{u})_D^{(B)}\}\) and \(\{(\hat{\mathcal {S}}^*_u)_D^{(1)},\dots , (\hat{\mathcal {S}}^*_u)_D^{(B)}\}\).
-
1.1.
-
2.
Approximate the sample statistic \(\tilde{(E)}_D=\int _{\mathcal {D}} (T_{t})_D/(\hat{\mathcal {S}}_{t})_D dt\) value by means of numerical techniques using \(\{(T_{1})_D,\dots ,(T_{\mathcal {T}})_D\}\) and \(\{(\hat{\mathcal {S}}_{1})_D,\dots ,(\hat{\mathcal {S}}_{\mathcal {T}})_D\}\).
-
3.
For every \(b=1,\dots ,B\), approximate the bootstrap statistic value given by \((\tilde{E}^{*})^{(b)}_D=\int _{\mathcal {D}} (T^*_{t})^{(b)}_D/(\hat{\mathcal {S}}^*_t)^{(b)}_D dt\), by means of numerical techniques using \(\{(T^{*}_{1})_D^{(b)},\dots ,(T^{*}_{\mathcal {T}})_D^{(b)} \}\) and \(\{(\hat{\mathcal {S}}_1^{*})_D^{(b)},\dots ,(\hat{\mathcal {S}}_{\mathcal {T}}^{*})_D^{(b)} \}\).
-
4.
Obtain the bootstrap p-value as \(\frac{1}{B} \sum _{b=1}^{B} \mathbb {I}\{(\tilde{E}^{*})^{(b)}_D \ge (\tilde{E})_D\}\), where \(\mathbb {I}(\cdot )\) is the indicator function.
Moreover, the test is guaranteed to be powerful under local alternatives. A characterization of local alternatives is given in Section 1.7 of the supplementary material of Zhang et al. (2018). This result can be proved simply by plugging in the corresponding integrated versions in Theorem 2.4 of Zhang et al. (2018). This proof is omitted because of the extension.
In terms of D, a particular case is to consider all covariates, \(D=\{1,\dots ,p\}\). First of all, one must check if, at least, some covariates supply relevant information to model Y. Considering D the set of all covariates indices, we can verify this premise performing (10). In case of not having evidence to reject the null hypothesis of conditional mean independence, it does not make sense to model Y with the available information. Otherwise, if one discards the conditional mean independence in this initial step, one can be interested in searching for an efficient subset of covariates to reduce the problem dimension.
Then, for a subset \(D\subset \{1,\dots ,p\}\) with cardinality d, \(1\le d<p\), it is possible to test if these d covariates play a role in terms of the concurrent regression model by means of (10). If not, it is possible to discard them and reduce the problem dimensionality to \(p-d\). In case we are interested in covariates screening one by one, which corresponds with the case where \(D=\{j\}\), we can apply the \(j=1,\dots ,p\) tests displayed in (3). This results in p consecutive partial tests for \(j=1,\dots ,p\) considering \(H_{0j}:\mathbb {E} \left[ Y(t) \arrowvert _{X_j(t)} \right] =\mathbb {E} \left[ Y(t) \right] \) almost surely \(\forall t\in \mathcal {D}\setminus \mathcal {N}\) or equivalently \(H_{0j}:\widetilde{MDD}^2 \left( Y(t) \arrowvert _{X_j(t)} \right) =0\) almost surely \(\forall t\in \mathcal {D}{\setminus } \mathcal {N}\). One drawback of carrying out p consecutive tests is that the initial prefixed significance level is violated if this is not modified considering the total number of tests to be performed. As a result, the significance level has to be adequately corrected. Some techniques, such as the classic but conservative Bonferroni’s correction, or the false discovery rate alternative (see Benjamini and Yekutieli (2001), and Cuesta-Albertos et al. (2017)) can be easily applied to avoid this inconvenience.
3.1 Derivation of \(\widehat{\widetilde{\mathcal {S}}}^2\)
In this section, we prove that the estimator of the variance considered in (12) for the term \(\widetilde{MDD}_{n}^2(\mathbf {Y_n(t)}\arrowvert _{\mathbf {X_{nj}(t)}})= \int _{\mathcal {D}} MDD_{n}^2(\mathbf {Y_n(t)}\arrowvert _{\mathbf {X_{nj}(t)}})dt\) correctly estimates this quantity.
As mentioned above, \(\widetilde{MDD}_{n}^2(\mathbf {Y_n(t)}\arrowvert _{\mathbf {X_{nj}(t)}})\) is a \(\mathcal {U}\)-statistic of order four. This result implies that using the Hoeffding decomposition, this quantity can be expressed as
where \(\widetilde{U_j(x,x')}\) is equal to
and \(\widetilde{V(y,y')}=\int _{\mathcal {D}} (y-\mu _Y)^\top (y'-\mu _Y)dt\) for \(\mu _Y=\mathbb {E}[Y(t)]\), being \((\mathcal {R}_n)_j\) a remainder term.
Calculation about Hoeffding decomposition for our framework is collected in Section 2 of the Online Supplementary Material.
If we define the theoretical test statistic
considering \(\widetilde{\mathcal {S}}\) the true integrated version of the variance, we can see that
where \(D_{n,1}= \left( {\begin{array}{c}n\\ 2\end{array}}\right) ^{-1/2}\sum _{1\le k<l\le n} \sum _{j\in D} \widetilde{U_j(X_{kj}(t),X_{lj}(t))} \cdot \widetilde{V(Y_k(t),Y_l(t))}\) is the leading term and \(D_{n,2}=\left( {\begin{array}{c}n\\ 2\end{array}}\right) ^{1/2} \sum _{j\in D} (\mathcal {R}_n)_j\) is the remainder one. Under the \(H_0\) assumption of (2) it is verified that
Since the contribution from the term \(D_{n,2}\) is asymptotically negligible, we may set \(\widetilde{\mathcal {S}}^2=\mathbb {V}\left[ D_{n,1} \right] \), and then construct the variance estimator displayed in Eq. (12).
3.2 Some missing points in curves trajectories
Until now, we have worked under the assumption that complete curve trajectories were observed. In contrast, in this part, some missing points are allowed. Then, for each time point \(t_u\) there are \(1\le n_u\le n\) observed samples of the form \(\{Y_{i_u}(t_u),X_{i_u}(t_u)\}_{i_u=1}^{n_u}\). A graphic example for the case considering \(q=1\) and \(p=2\) covariates is displayed in the first row of Fig. 2. In this example, we have \(n=5\) curves and a different number of observations. For instance, there are \(n_1=4\) points for \(t_1\).
First row: sample of five curves measured at different time instants \(\{t_u\}_{u=1}^{\mathcal {T}}\in \mathcal {D}\) considering \(p=2\) covariates (\(X_1(t)\) and \(X_2(t)\)) to explain Y(t). Second row: same example adding the recovered points by means of splines interpolation. Filled dots (\(\bullet \)) represent the \(n_u\) observed points at each instant \(t_u\) and asterisks ( ) the recovered ones
) the recovered ones
In this context, our proposed method cannot be applied directly. This is because it is not verified \(n_u=n\) for all \(u=1,\dots ,\mathcal {T}\). However, we can solve this problem by estimating the missing curve values when is possible. This option translates into a recovering of the whole curve trajectories on the grid \(\{t_u\}_{u=1}^{\mathcal {T}}\in \mathcal {D}\), verifying now that \(n_u=n\) for all \(u=1,\dots ,\mathcal {T}\).
A simple but efficient idea is to recover the complete trajectory of the curves using some interpolating method with enough flexibility. For example, making use of cubic spline interpolation ideas for each of the \(1,\dots ,n\) curves. Results of this recovery for our example are displayed in the second row of Fig. 2. In this case, the spline function of the stats library of the R software (R Core Team 2019) has been employed.
In addition, other approaches for recovering the missing points are also available. Next, we propose one based on functional basis representation following the guidelines of Kim et al. (2018), Ghosal et al. (2020), and Ghosal and Maity (2022b). If it is possible to assume that the total number of time observations \(\bigcup _{u=1}^\mathcal {T} t_u\) is dense in \(\mathcal {D}\), then the eigenvalues and eigenfunctions corresponding to the original curves can be estimated using functional principal component analysis (see Yao et al. (2005)). We refer to Yao et al. (2005) for more details about the procedure. As a result, one can get the estimated trajectory \(\hat{X}_{ij}(\cdot )\) of the true curves \(X_{ij}(\cdot )\) for \(i=1,\dots ,n\) and \(j=1,\dots ,p\), given by \(\hat{X}_{ij}(t)=\hat{\mu }_j(t)+\sum _{q=1}^{Q} \hat{\zeta }_{iqj} \hat{\Psi }_{qj}(t)\). Here, Q denotes the number of considered eigenfunctions, which can be chosen using a predetermined percentage of explained variance criterion. Consequently, it is possible to recover the value of \(X_1(\cdot ),\dots ,X_p(\cdot )\) on all grid \(\{ t_u \}_{u=1}^\mathcal {T} \in \mathcal {D}\). In the same way, the values of \(Y_1(\cdot ),\dots ,Y_q(\cdot )\) can also be recovered. Thus, it is possible to work again in the context of synchronously measured data. This procedure is implemented in the fpca.sc function belonging to the library refund of R (see Goldsmith et al. (2021)). For our proposed naive example, we have obtained similar results to the splines interpolation methodology displayed in Fig. 2. As a result, these are omitted.
4 Simulation studies
In this section, we consider two simulated concurrent model scenarios to assess the performance in the practice of the new significance tests introduced above. We distinguish between linear (Scenario A) and nonlinear (Scenario B) formulation of the model (1). For the sake of simplicity, we consider only the case where the data are measured at the same instants of time. For this aim, a Monte Carlo study with \(M=2000\) replicas in each case is performed using the R software (R Core Team 2019). Besides, we compare the performance of our test with two competitors. These are the procedure introduced in Ghosal and Maity (2022a), developed in the linear framework, and the method of Kim et al. (2018) for the additive formulation. Henceforth, we refer to them by FLCM and ANFCM, respectively. We refer to Section A of the Appendix for more details about competitors’ implementation.
-
Scenario A (Linear model): We assume linearity in (1), take \(t\in \mathcal {D}=[0,1]\) and consider \(q=1\) and \(p=2\) covariates entering the model. As a result, the simulated model is given by the structure
$$\begin{aligned} Y(t)=\beta _1(t)X_1(t)+\beta _2(t)X_2(t)+\varepsilon (t) \end{aligned}$$with
$$\begin{aligned} X_1(t)=5\sin \left( \frac{24\pi t}{12}\right) +\varepsilon _1(t),\quad X_2(t)=\frac{-(24t-20)^2}{50}-4+\varepsilon _2(t). \end{aligned}$$Here, \(\beta _1(t)=-\left( \frac{24t-15}{10}\right) ^2-0.8\) and \(\beta _2(t)=0.01((24t-12)^2 - 12^2 +100 )\). The error terms represented by \(\varepsilon _1(t), \varepsilon _2(t)\) and \(\varepsilon (t)\) are simulated as random Gaussian processes with exponential variogram \(\Omega (s,t)=0.1 \exp { \left( -\frac{24|s-t|}{10} \right) }\). We assume that a total number of \(\mathcal {T}=25\) equispaced instants are observed in \(\mathcal {D}=[0,1]\) (\(\{t_u\}_{u=1}^{25}\)) and there are \(n=20,40,60,80,100\) curves available for each of them. An example of these functions is displayed in Fig. 3. We remark that we have not included intercept in our linear formulation because this can be done without loss of generality just centering both Y(t) and \(X(t)=(X_1(t),X_2(t))^\top \in \mathbb {R}^2\) for all \(t\in \mathcal {D}\).
-
Scenario B (Nonlinear model): A nonlinear structure of (1) is assumed for this scenario. Again, we take \(t\in \mathcal {D}=[0,1]\) and consider \(q=1\) and \(p=2\) covariates to explain the model. Then, this model has the expression
$$\begin{aligned} Y(t)=F_1(t,X_1(t))+F_2(t,X_2(t))+\varepsilon (t) \end{aligned}$$being \( F_1(t,X_1(t))=\exp ((24 t+1) X_1(t)/20)-2\) and \(F_2(t,X_2(t))=-1.2\log (X_2(t)^2) \sin (2\pi t)\), with \(X_1(t)\) and \(X_2(t)\) equally defined as in the linear case (Scenario A) and using the same observed discretization time points. Now, the errors \(\varepsilon _1(t), \varepsilon _2(t)\) and \(\varepsilon (t)\) are assumed to be random Gaussian processes with exponential variogram \(\Omega (s,t)=0.02 \exp { \left( -\frac{24|s-t|}{10} \right) }\). An example of this scenario is displayed in Fig. 4.
In all tests, we make use of the wild bootstrap techniques introduced above in Sect. 3 to approximate the p-values. We have employed \(B=1000\) resamples on each case. Besides, as we mentioned before, sample test size and power are obtained by Monte Carlo techniques. In order to know if the p-values under the null take an adequate value, the \(95\%\) confidence intervals of the significance levels are obtained by making use of expression \(\left[ \alpha \mp 1.96 \sqrt{\frac{\alpha (1-\alpha )}{M}} \right] \). Here, \(\alpha \) is the expected level and M is the number of Monte Carlo simulated samples. As a result, we consider that a p-value is acceptable for levels \(\alpha =0.01,0.05,0.1\) if this is within the values collected in Table 1 for the Monte Carlo replicates. We highlight the values out of these scales in bold for simulation results.
4.1 Results for scenario A (linear model)
We start analyzing the performance of the global mean dependence test in the linear model formulation, using Scenario A introduced above in Sect. 4. For this purpose, we consider three different scenarios. In the first one, the null hypothesis of mean independence is verified by simulating under the assumption that \(\beta _1(t)=\beta _2(t)=0\). Next, the remaining two cases are simulated under the alternative hypothesis. This claims that information provided by \(X(t)=(X_1(t),X_2(t))^\top \) is useful in some way: only the \(X_2(t)\) covariate is relevant (fixing \(\beta _1(t)=0\)) or both covariates \(X_1(t)\) and \(X_2(t)\) support relevant information to correctly explain Y(t).
Obtained results are collected in Table 2 for \(n=20,40,60,80,100\). In view of the results, it is appreciated as the empirical sizes approximate the significance levels under \(H_0\) (\(H_0:\beta _1(t)=\beta _2(t)=0\)) as n increases. Moreover, the empirical distribution of the p-values seems to be a U[0, 1] as it is appreciated in Fig. 8 of Section B of the Appendix. In contrast, simulating under the alternative hypothesis, \(H_a:\beta _1(t)=0,\beta _2(t)\not =0\) and \(H_a:\beta _1(\mathfrak {t})\not =0, \beta _2(\mathfrak {t})\not =0\) scenarios, the test power tends to one as the sample size increases. As a result, we can claim that the test is well-calibrated and has power.
Once we have rejected the null hypothesis that all covariates are irrelevant in practice, we can detect which of them play a role in terms of data explanation. For this aim, partial tests can be carried out, testing if every covariate is irrelevant, \(H_{0j}:\beta _j(t)=0 \; \forall t \in \mathcal {D}\), or not, \(H_{aj}:\beta _j(t)\not =0 \; \text {for some } t \in \mathcal {V}\), being \(j=1,\dots ,p\).
Again, we consider different scenarios. First of all, it is assumed that X(t) is not significant taking \(\beta _1(t)=\beta _2(t)=0\). Then, we move to the situation where only \(X_2(t)\) is relevant. Finally, we consider the model including both \(X_1(t)\) and \(X_2(t)\) effects to explain Y(t). Results of these scenarios are displayed in Table 3. Here, we appreciate as the empirical sizes tend to the significance levels simulating under the null hypothesis that both covariates have not got a relevant effect on the response, separately. Besides, we see as in case of having \(\beta _1(t)=0\) and \(\beta _2(t)\not =0\), these tests help us to select relevant information, \(X_2(t)\), and discard noisy one, \(X_1(t)\). Otherwise, when both covariates are relevant, the partial tests clearly reject the \(H_{0j}\) hypothesis of null effect, tending their powers to the unit as sample size increases.
4.2 Results for scenario B (nonlinear model)
In this section, we analyze the performance of the MDD global mean independence test in a more difficult framework: a nonlinear effects formulation. For this purpose, Scenario B introduced in Sect. 4 is employed. Again, three different situations of dependence are considered, following the same arguments of Sect. 4.1. As a result, we simulate under the no effect case (\(H_0:F_1(t, X_1(t))=F_2(t, X_2(t))=0\)), which corresponds with independence, and two dependence frameworks: where only one covariate is relevant (\(H_a:F_1(t, X_1(t))=0, F_2(t, X_2(t))\not =0\)) or both of them are (\(H_a:F_1(t, X_1(t))\not =0, F_2(t, X_2(t))\not =0\)).
Results of the \(M=2000\) Monte Carlo simulations for the MDD-test taking \(n=20,40,60,80,100\) are displayed in Table 4. We appreciate simulating under the null hypothesis \(H_0\) that the p-values tend to stabilize around the significance levels. Figure 9, collected in Section B of the Appendix, shows as these seem to follow a uniform distribution in [0, 1]. So, we can conclude that our test is well calibrated even for nonlinear approaches. Concerning the power, when the independence assumption is violated, the p-values tend to 1 as the sample size increases. Two examples of this phenomenon are displayed in Table 4 simulating the different alternative hypotheses. Summing up, our proposal is also a well-calibrated and powerful test in a nonlinear framework.
Next, our interest focuses on partial tests to apply covariates selection in this nonlinear scenario. Again, we consider the three different dependence scenarios introduced above. However, we test the independence for each covariate separately. This results in applying a total of \(j=1,\dots ,p\) tests. In this way, we expect the test in a situation as \(F_1(t, X_1(t))=0\), \(F_2(t, X_2(t))\not =0\) to be capable of detecting relevant covariates (\(X_2(t)\)), rejecting its corresponding \(H_{0j}\) hypothesis, and excluding noisy ones from the model otherwise (\(X_1(t)\)). Results for partial tests are collected in Table 5. One can see as these tests allow us to determine which covariates play a relevant role in each scenario, being those with p-values higher than the significance levels and tending to 1 as sample size increases. Conversely, those verifying that its associated p-values are less or equal to significance levels are assumed irrelevant.
4.3 Comparison with FLCM and ANFCM algorithms
Next, our novel procedure is compared with existing competitors in the literature. For this aim, we have considered the FLCM algorithm of Ghosal and Maity (2022a) for the linear framework and the ANFCM procedure of Kim et al. (2018) for a more flexible model, assuming additive effects. Both have displayed excellent results in practice considering a proper selection of the tuning parameters. We refer the reader to Appendix A for more details.
In the simulation scenarios introduced in Sect. 4, we consider a dependence structure where all instants relate between them. This structure emulates a real functional dataset. Nevertheless, this does not apply in the simulation scenarios of Ghosal and Maity (2022a) and Kim et al. (2018). Conversely, they consider independent errors. As a result, to perform a fair competition, we start analyzing the behavior of our MDD-based tests in their simulation scenarios. Specifically, we compare the performance of our proposal with the results of FLCM in Scenario A of Ghosal and Maity (2022a). Next, we implement a comparison with the ANFCM procedure. For this purpose, we consider Scenario (B) of Kim et al. (2018), taking the error \(\text {E}^3\). In this last case, we implement a modification to perform Algorithm 1. In particular, we only consider the second covariate associated with the nonlinear effect. In both borrowed scenarios, we simulate under the dense assumption being \(\{t_u\}_{u=1}^{81}\) a total of \(m=81\) equidistant time points in [0, 1]. We keep the authors’ parameters selection and perform a Monte Carlo study with \(M=1000\) samples in all cases, obtaining the p-values through \(B=200\) bootstrap replicates. Besides, following the author’s recommendation after a preliminary study to determine the optimal number of basis functions for these examples, we work with 7 components for FLCM and ANFCM procedures. More details can be found in Ghosal and Maity (2022a) or Kim et al. (2018), respectively. We remind the structure of the scenarios and explain implementation issues in Section A of the Appendix.
Results of the comparison between FLCM and MDD effect tests for scenario A of Ghosal and Maity (2022a) are collected in Table 6. We appreciate that simulating under the null (\(d=0\)), one value of the FLCM algorithm is out of the \(95\%\) confidence interval. In contrast, the MDD procedure does not suffer from this issue. Moreover, paying attention to the p-values distributions under the null, which are displayed in Fig. 10 (see Section B of the Appendix), one can see the FLCM p-values do not follow a uniform distribution. In contrast, the MDD-based test corrects this phenomenon. As a result, it seems that our test provides a better calibration than the FLCM approach. Regarding the power, levels for both algorithms tend to 1 as sample size increases, and their values are higher for the \(d=7\) scenario than for the \(d=3\) one, as would be expected. Now, the FLCM algorithm outperforms the MDD results in all scenarios. However, our procedure is still quite competitive even considering that the data are simulated under the linear assumption, giving an advantage to the FLCM procedure.
Next, we compare the performance of the MDD with the ANFCM approach in an additive framework. Table 7 collects the simulation results for both procedures. We can see as both methodologies are well calibrated under the null (\(d=0\)) for all levels, except for the \(1\%\), where their values are out of the \(95\%\) confidence interval for \(n=60\). Nevertheless, taking greater values of n, as \(n=100\), solves this issue. Moreover, simulating under \(H_0\), the p-values follow a uniform distribution. This is illustrated in Fig. 11 displayed in Section B of the Appendix. If we simulate under the alternative hypotheses (\(d=3\) and \(d=7\)), we see that these quantities tend to 1 as the sample size increases. In addition, as the covariate effect becomes more noticeable, going from \(d=3\) to \(d=7\), the power of ANFCM and MDD procedures increases. Again, the power of the ANFCM algorithm is always higher than the MDD one. At this point, we should notice that the ANFCM algorithm takes advantage of the fact that an additive structure with an intercept function is assumed. In contrast, our MDD test does not consider any model structure, not even the inclusion of intercept in the model. As a result, our competitor has to measure all possible forms of departure from conditional mean independence.
It is relevant to notice that, in both previous scenarios, covariates are related to the response employing trigonometric functions when it corresponds. Then, modeling the effects takes advantage of the B-spline basis representation. In addition, the errors are assumed to be time-independent between them in the FLCM and ANFCM scenarios. These considerations are a clear advantage for the FLCM and the ANFCM algorithms compared to our procedure. Thus, to test the FLCM and ANFCM performance in a functional context with time-correlated errors and when the model structure does not depend on only trigonometric functions, we apply these to the simulation scenarios introduced in Sect. 4. For this purpose, a partial approach is considered, testing the effect of the covariates separately using the FLCM procedure in Scenario A and the ANFCM one in Scenario B. To compare our results with theirs, we simulate now \(M=2000\) Monte Carlo replications and use \(B=1000\) bootstraps resamples for ANFCM. Again, we follow the authors’ recommendation and use \(Q=7\) basis terms in both procedures.Footnote 1 We refer to Section A of the Appendix for a summary of the simulation parameters selection.
Results of partial FLCM tests in scenario A are displayed in Table 8. It can be seen how, regardless of the size of the sample used, the test is always poorly calibrated. In fact, all obtained p-values are out of the \(95\%\) confidence intervals. These results contrast with the MDD ones displayed in Table 3, where the test is well calibrated. This phenomenon may be because, as mentioned above, it is considered a different dependence structure more related to a functional nature. In terms of power, there is not a clear winner. Our test is more powerful in the \(H_a:\beta _1(t)=0,\; \beta _2(t)\not =0\) scenario in test \(H_{02}\), but FLCM is a bit more powerful in the last scenario for \(H_{02}\). However, this difference is small, and considering that the FLCM is not well calibrated, it makes sense to conclude that the MDD-based procedure outperforms this.
Next, the performance of the ANFCM algorithm is tested by simulating under Scenario B of Sect. 4. Results are collected in Table 9. Again, comparing the ANFCM results with the ones of the MDD test (Table 5), we see that the MDD test is well calibrated even for small values as \(n=20\) (except for a couple of cases). This fact contrasts with the results of the ANFCM procedure. In this last, most of the values are out of the \(95\%\) confidence intervals. Moreover, the MDD test has more power than ANFCM in almost all cases. As a particularity, the ANFCM algorithm is not able to detect the relevance of \(X_2(t)\) in the \(H_a:F_1(\cdot )=0,\; F_2(\cdot )\not =0\) scenario. Instead, the percentage of rejections is around the significance values and does not provide significant evidence to reject the null hypothesis \(H_{02}\) of independence. Thus, we can conclude that the MDD outperforms the ANFCM procedure.
In summary, we have proved that the MDD algorithm performs pretty well in scenarios where the FLCM and the ANFCM procedures have an advantage, considering uncorrelated errors and trigonometric functions. Moreover, our test outperforms these when we move on to a more functional context, as in scenarios A and B introduced in Sect. 4. In these scenarios, we consider related errors and other types of relations different from trigonometric functions.
5 Real data analysis
In this section, we test the performance of the proposed algorithms in three real datasets. Firstly, the well-known gait dataset of Olshen et al. (1989) is considered. This dataset is an example of a linear effects model and has already been studied in the concurrent model framework in works as the one of Ghosal and Maity (2022a) or Kim et al. (2018). Next, a google flu database from the USA, borrowed from Wang et al. (2017), is studied. In this work, Wang et al. (2017) assume a linear formulation to model the data. Eventually, an example of a model with nonlinear effects and some missing points is studied. For this purpose, the bike sharing dataset of Fanaee-T and Gama (2014) is analyzed. Obtained results are compared with the ones of Ghosal and Maity (2022b) in this concurrent model framework.
5.1 Gait data
Here, we analyze the performance of the new dependence test in a well-known dataset from the functional data context. These data are the gait database (Olshen et al. 1989; Ramsay and Silverman 2005), in which the objective is to understand how the joints in the hip and the knee interact during a gait cycle in children. This problem has already been studied in the concurrent model context using a different methodology (see Ghosal and Maity (2022a), or Kim et al. (2018)). As a consequence, we compare our results with theirs.
The data consist of longitudinal measurements of hip and knee angles taken on 39 children with gait deficiency. These are measured as they walk through a single gait cycle. These data can be found in the fda library (Ramsay et al. 2020) of the R software (R Core Team 2019). The hip and knee angles are measured at 20 evaluation points \(\{t_u\}_{u=1}^{20}\) in [0, 1]. These values correspond to the completed percentage of a single gait cycle. Following previous studies, we have considered as response Y(t) the knee angle and as explanatory covariate X(t) the hip angle. Data are displayed in Fig. 5.
Applying our dependence test, we obtain a p-value close to 0. Thus, we have strong enough evidence to reject the independence hypothesis to the usual significance levels. This conclusion translates into a dependency between knee and hip angle in one cycle of gait data in children with poor gait. This result agrees with the ones of Kim et al. (2018) or Ghosal and Maity (2022a), among others, in the concurrent model framework. They obtain p-values less than 0.004 and 0.001, respectively. Summing up, the hip angle measured at a specific time point in a gait cycle has an effect on the knee angle at the same time point in children.
5.2 Google flu data from USA
Google flu data are used in Wang et al. (2017) to model the relationship between flu activity and temperature fluctuation in the USA. For this purpose, influenza-like illness (ILI) cases per 100000 doctor visits are considered in the 2013-2014 flu season (July 2013-June 2014). This information is got from the Google flu trend Website. Moreover, daily maximum and minimum temperature averaged over weather stations within each continental state is obtained by means of the US historical climatology network. The daily temperature variation (MDTV) is considered the explanatory covariate, being the difference between the daily maximum and daily minimum. The temperature fluctuation is aggregated to the same resolution as the flu activity data by taking the MDTV each week. Only 42 states are considered due to missed records. We refer to Wang et al. (2017) for more details.
The original dates from July 1st, 2013, to June 30th, 2014, were numbered by integers from 1 to 365. Then, time t is rescaled to the [0, 1] interval by dividing the numbers by 365. Besides, we consider regional effects by dividing the data into four sets in terms of midwest, northeast, south, or west region to study them separately. Following Wang et al. (2017), the ILI percentage and MDTV are standardized at each time point t by dividing the variables by their root mean squares. Data of study are shown in Fig. 6 separating this by the considered regions.
Therefore, we want to test if the MDTV has relevant information in the flu tendency modeling of the four considered regions. For this aim, we can apply a global test for each one separately. Results of dependence tests are displayed in Table 10. In view of all p-values being higher than 0.1, we can conclude that we do not have enough evidence to reject the null hypothesis of mean conditional independence for levels as \(10\%\). As a result, the MDTV does not play a relevant role in the ILI modeling, no matter the US region. We can argue that perhaps the regional effect is unimportant, and we should consider the data as a whole. For this purpose, we implement a global test considering all the states, obtaining a p-value close to 0. This result highlights that there is strong evidence to reject the conditional mean independence between MDTV and ILI. As a result, MDTV provides notable information to explain the ILI behavior, but this is equal in the four considered regions, so a distinction does not make sense.
Our results agree with the ones of Wang et al. (2017). First, they reject the location effect for the linear model formulation. Secondly, they claim that one can avoid the MDTV covariate from the linear model for a \(10\%\) significance level but not for the \(5\%\) (p-value=0.052). Thus, they have moderately significant evidence that the MDTV plays a role in the ILI explanation, at least in the linear context. It is important to remark that differences may be because they assume linearity in their regression model. Furthermore, a first preprocessing step is applied in their case to remove spatial correlations.
5.3 Bike sharing data
Next, a bike-sharing dataset of the Washington, D.C., program is analyzed. This is introduced in Fanaee-T and Gama (2014). The data are obtained daily by the Capital bike-share system in Washington, D.C., from 1 January 2011 to 31 December 2012. The aim is to explain the number of casual rentals in terms of meteorological covariates. As a result, this dataset contains information on casual bike rentals in the cited period along with other meteorological variables such as temperature in Celsius (temp), the feels-like temperature in Celsius (atemp), relative humidity in percentage (humidity), and wind speed in Km/h (windspeed) on an hourly basis. In particular, only the data corresponding with Saturdays are considered because of the dynamic changes between working and weekend days. This selection results in a total of 105 Saturdays barring some exceptions (8 missings). All covariates are normalized by formula \((t-t_{\min })/(t_{\max }-t_{\min })\) in case of temp and atemp, and these are divided by the maximum for the humidity and windspeed case. In order to correct the skewness of the hourly bike rentals distribution (Y(t)), a log transformation is applied considering as response variable \(Y(t)=log(Y(t)+1)\). These are showed in Fig. 7.
First, the missing data are recovered employing splines interpolation as described in Sect. 3.2. Then, once we have a total of \(n=105\) data points at each time instant, the global significance MDD-based test is performed. We obtain a p-value close to 0, which rejects the null hypothesis of independence for usual significant levels as the \(5\%\) or the \(1\%\).
Next, we perform partial tests to detect if any of the four considered covariates (temp, atemp, humidity, and windspeed) can be excluded from the model. We obtain p-values of 0, 0, 0.007, and 0.001 for temperature (temp), feels-like temperature (atemp), relative humidity (humidity), and wind speed (windspeed), respectively. Thus, we can claim that all of these affect the number of casual rentals at significance levels as the \(1\%\). This last result agrees with other studies, like the one of Ghosal and Maity (2022b). In this study, different covariates are selected by the distinct considered penalizations. In an overview of their results, each covariate is selected at least two times over the five considered procedures. As a result, all covariates seem to play a relevant role separately.
6 Discussion
We propose novel significance tests for the additive functional concurrent model, which collects a wide range of different structures between functional covariates and response. As a result, the relevance of a subset of covariates to model the response in a regression setting is tested, including global and partial tests to apply covariates screening. This approach allows one to detect irrelevant variables and reduce the problem dimensionality, facilitating the subsequent estimation procedure. For this aim, we construct test statistics based on MDD insights and taking into consideration all observed time instants. This process results in general significance tests able to determine the covariates’ relevance over the complete trajectory. In contrast with existing methodology in literature for significance tests in the concurrent model, as the FLCM (Ghosal and Maity 2022a) or the ANFCM (Kim et al. 2018) procedures among others, our approach has the novel property that there is no need of a preliminary estimation of the model structure. Besides, this new procedure allows multivariate responses \(Y(t)\in \mathbb {R}^q\) for \(q\ge 1\) and \(t\in \mathcal {D}\). Furthermore, no tuning parameters are involved in contrast with previous methodologies. Instead, it is only needed to compute a \(\mathcal {U}\)-statistic version of the MDD to be able to apply the tests. Using the theory of \(\mathcal {U}\)-statistics, good properties of this estimator are guaranteed in practice, as its unbiasedness. In addition, its asymptotic distribution is obtained both under the null and local alternative hypotheses. Eventually, bootstrap procedures are implemented to obtain its p-values in practice.
The new tests proposed have displayed good performance in linear formulations as well as in nonlinear structures. This is appreciated by means of the results of scenarios A and B considered in the simulation study of Sect. 4. These procedures are well calibrated under the null hypothesis of no effect, tending to the significance level as the sample size increases. Moreover, they have power under alternatives, which one can deduce from observing that p-values tend to the unit as sample size increases when associated covariates are relevant. Besides, these procedures seem to perform well in real datasets too. We display an example of this result in Sect. 5, where we analyze three real datasets. Other authors have already studied these, so we compare our outcomes with existing literature, obtaining similar results when these are comparable. As a result, the MDD-based test is a pretty transversal tool to detect additive effects in the concurrent model framework without the need for previous assumptions or model structure estimation. Moreover, notice that all these ideas could be extended to conditional quantile dependence testing in the concurrent model framework. For this purpose, a similar development would be enough, following the guidelines and adapting the ideas of Section 3 in Zhang et al. (2018).
In terms of performance comparison with existing literature, the MDD-based test methodology is put together with Ghosal and Maity (2022a) (FLCM) and Kim et al. (2018) (ANFCM) algorithms in the linear and additive model framework, respectively. Based on the obtained results, it is possible to claim that the new procedure is quite competitive. Even when the FLCM and ANFCM procedures have the advantage of being implemented assuming the correct model structure and an optimal number of the basis components, the new procedure results are comparable to theirs. These results arise in Sect. 4.3. In contrast, our procedure outperforms their results by simulating a more functional scenario and avoiding only trigonometric expressions in the model. Besides, another disadvantage of the competitors is that m(t, X(t)) is unknown in practice, so a misguided assumption of the model structure could lead to poor results. In addition, as discussed in Ghosal and Maity (2022a) and Kim et al. (2018), a suitable selection of the number of the basis components is problematic in practice. This issue is still an open problem. This quantity plays the role of tuning parameter, so an appropriate value is needed to guarantee a proper adjustment. In contrast, our proposal has the novelty that this does not require previous estimation or tuning parameters selection. Our approach bridges a gap and solves the problems mentioned above.
One limitation of the present form of our test is that this only admits the study of numerical covariates. This restriction is quite common for the concurrent model framework. Some examples are the works of Ghosal and Maity (2022a) or Kim et al. (2018). If one wants to be able to include categorical variables, as in other works such as in Wang et al. (2017), a different metric is needed to correctly define the \(\mathcal {U}\)-statistic of the MDD test. Some solutions for this problem have already been proposed for the distance covariance approach in the presence of noncontinuous variables. Similar ideas could be translated to the MDD context to solve this issue. An option is to extend the ideas proposed in Lyons (2013) for general metric spaces to this case. We leave this topic for future research.
Another drawback is related to the disposal of the observed time instants. It is necessary to monitor the same number of curves at each instant of time to be able to construct our proposed statistic. This restriction translates into synchronous observations with \(n_t=n\) points of the observed curves for all \(t\in \mathcal {D}\). When the number of missed points is small, we can impute these using interpolation techniques. An example is given in Sect. 3.2. However, in a sparse context where one observes each curve in a different number of time points, and these measures may not agree (asynchronous pattern), it is not possible preprocessing the data to obtain our starting point. Therefore, we need a new methodology based on different dependence measures. This problem is a pretty interesting area of study for future work. Concerning the observed time points, an additional drawback is the statistics computational time, being of the order of \(O(n(n-1)(n-2)(n-3)\mathcal {T})\) operations. Then, this procedure is quite competitive for “moderate” values of n and \(\mathcal {T}\). However, for large values of these quantities, especially those related to n, the statistic has a high computational cost. Consequently, simplification techniques in the number of required operations are of interest to make the procedure more tractable.
Eventually, we remark that our tests only collect additive effects. This phenomenon is due to the statistics structure displayed in (11). Although this formulation embraces a wide variety of different structures, this does not consider some complex relations. An example is the detection of possible interactions without a prespecified definition of a new variable collecting this information. Nevertheless, we think that our ideas can be extended to the general concurrent model formulation by resorting to projection techniques. Another interesting idea, pointed out by one of the referees, is to directly consider the integral of the vectorial version of the MDD coefficient and adapt the theoretical results of Székely et al. (2007). This expansion would translate into studying the convergence of the integrated version of an infinity family of empirical processes. Nevertheless, this procedure is not straightforward in this context. Both approaches are entirely new lines for future research that would need further study.
Change history
05 May 2023
A Correction to this paper has been published: https://doi.org/10.1007/s11749-023-00863-0
Notes
In this setup, we have \(\mathcal {T}=25\) time instants. Then, for the ANFCM procedure, as the function fpca.face employs by default a total of 35 knots to carry out FPCA, we have to reduce this. We decided to take 12 knots to solve this issue.
We have adapted the code to correctly generate X1(t) and Y(t). In particular, in the
 function, we have changed
function, we have changed  for the expression
for the expression  to correct a typo. Besides, it is needed to change
to correct a typo. Besides, it is needed to change  by
by 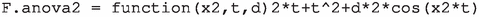 as well as
as well as  by
by  in function anova.datagen to correctly define the modified version.
in function anova.datagen to correctly define the modified version.
References
Benjamini Y, Yekutieli D (2001) The control of the false discovery rate in multiple testing under dependency. Ann Stat. https://doi.org/10.1214/aos/1013699998
Cuesta-Albertos J, García-Portugués E, Febrero-Bande M et al (2017) Goodness-of-fit tests for the functional linear model based on randomly projected empirical processes. Ann Stat. https://doi.org/10.1214/18-AOS1693
Fan J, Li R (2001) Variable selection via nonconcave penalized likelihood and its oracle properties. J Am Stat Assoc 96(456):1348–1360. https://doi.org/10.1198/016214501753382273
Fanaee-T H, Gama J (2014) Event labeling combining ensemble detectors and background knowledge. Lect Notes Artif Int 2:113–127. https://doi.org/10.1007/s13748-013-0040-3
Ghosal R, Maity A (2022) A score based test for functional linear concurrent regression. Econom Stat 21:114–130. https://doi.org/10.1016/j.ecosta.2021.05.003
Ghosal R, Maity A (2022) Variable selection in nonparametric functional concurrent regression. Canad J Statist 50(1):142–161. https://doi.org/10.1002/cjs.11654
Ghosal R, Maity A, Clark T et al (2020) Variable selection in functional linear concurrent regression. J R Stat Soc Ser C Appl Stat 69(3):565–587. https://doi.org/10.1111/rssc.12408
Goldsmith J, Schwartz JE (2017) Variable selection in the functional linear concurrent model. Stat Med 36(14):2237–2250. https://doi.org/10.1002/sim.7254
Goldsmith J, Scheipl F, Huang L et al (2021) Refund: regression with functional data. https://CRAN.R-project.org/package=refund, r package version 0.1-24
Jiang C, Wang J (2011) Functional single index models for longitudinal data. Ann Statist 39(1):362–388. https://doi.org/10.1214/10-AOS845
Kim J, Maity A, Staicu AM (2018) Additive nonlinear functional concurrent model. Stat Interface 11:669–685. https://doi.org/10.4310/SII.2018.v11.n4.a11
Lee AJ (1990) U-Statistics: theory and practice. statistics: textbooks and monographs, New York, https://doi.org/10.1201/9780203734520
Lyons R (2013) Distance covariance in metric spaces. Ann Probab 41(5):3284–3305. https://doi.org/10.1214/12-AOP803
Maity A (2017) Nonparametric functional concurrent regression models. Wiley Interdiscip Rev Comput Stat 9(2):e1394. https://doi.org/10.1002/wics.1394
Olshen RA, Biden EN, Wyatt MP et al (1989) Gait analysis and the bootstrap. Ann Statist 17(4):1419–1440. https://doi.org/10.1214/aos/1176347372
Ospína-Galindez J, Giraldo R, Andrade-Bejarano M (2019) Functional regression concurrent model with spatially correlated errors: application to rainfall ground validation. J Appl Statist 46(8):1350–1363. https://doi.org/10.1080/02664763.2018.1544231
Park T, Shao X, Yao S (2015) Partial martingale difference correlation. Electron J Stat 9:1492–1517. https://doi.org/10.1214/15-EJS1047
R Core Team (2019) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria, https://www.R-project.org/
Ramsay JO, Silverman BW (2005) Functional data analysis. Springer, New York. https://doi.org/10.1007/978-1-4757-7107-7
Ramsay JO, Graves S, Hooker G (2020) FDA: Functional Data Analysis. https://CRAN.R-project.org/package=fda, r package version 5.1.9
Shao X, Zhang J (2014) Martingale difference correlation and its use in high-dimensional variable screening. J Am Stat Assoc 109(507):1302–1318. https://doi.org/10.1080/01621459.2014.887012
Szekely GJ, Rizzo ML (2017) The energy of data. Annu Rev Stat Appl 4:447–479. https://doi.org/10.1146/annurev-statistics-060116-054026
Székely GJ, Rizzo ML, Bakirov NK (2007) Measuring and testing dependence by correlation of distances. Ann Statist 35(6):2769–2794. https://doi.org/10.1214/009053607000000505
Tibshirani R (1996) Regression shrinkage and selection via the LASSO. J R Stat Soc B 58(1):267–288. https://doi.org/10.1111/j.2517-6161.1996.tb02080.x
Wang H, Zhong P, Cui Y et al (2017) Unified empirical likelihood ratio tests for functional concurrent linear models and the phase transition from sparse to dense functional data. J R Stat Soc B 80(2):343–364. https://doi.org/10.1111/rssb.12246
Xue L, Zhu L (2007) Empirical likelihood for a varying coefficient model with longitudinal data. J Am Stat Assoc 102(478):642–654. https://doi.org/10.1198/016214507000000293
Yao F, Müller H, Wang J (2005) Functional data analysis for sparse longitudinal data. J Am Stat Assoc 100(470):577–590. https://doi.org/10.1198/016214504000001745
Yuan M, Lin Y (2006) Model selection and estimation in regression with grouped variables. J R Stat Soc B 68(1):49–67. https://doi.org/10.1111/j.1467-9868.2005.00532.x
Zhang C (2010) Nearly unbiased variable selection under minimax concave penalty. Ann Statist 38(2):894–942. https://doi.org/10.1214/09-AOS729
Zhang J, Clayton M, Townsend P (2011) Functional concurrent linear regression model for spatial images. J Agric Biol Environ Stat 16:105–130. https://doi.org/10.1007/s13253-010-0047-1
Zhang X, Yao S, Shao X (2018) Conditional mean and quantile dependence testing in high dimension. Ann Statist 46(1):219–246. https://doi.org/10.1214/17-AOS1548
Acknowledgements
We want to sincerely acknowledge the work of the associated editor and two anonymous referees. Specifically, we thank them for their insightful and constructive comments. These have helped us to improve the quality of the manuscript and to consider interesting extensions for future research. We also want to acknowledge Rahul Ghosal for his generosity in providing the code for the FLCM algorithm. The research of Laura Freijeiro-González is supported by the Consellería de Cultura, Educación e Ordenación Universitaria along with the Consellería de Economía, Emprego e Industria of the Xunta de Galicia (project ED481A-2018/264). Laura Freijeiro-González, Wenceslao González-Manteiga and Manuel Febrero-Bande acknowledged the support from Project PID2020-116587GB-I00 funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe” and the Competitive Reference Groups 2021-2024 (ED431C 2021/24) from the Xunta de Galicia through the ERDF. We also acknowledge the Centro de Supercomputación de Galicia (CESGA) for computational resources.
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
“The original online version of this article was revised: In Section 4, figures 3 and 4 were conversely cited. Figure 3 has to be cited in Scenario A (Linear model) and Figure 4 in Scenario B (Nonlinear model).”
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary information:
The online version contains supplementary material with proofs of some results. In addition, code for simulations and real data sets analysis is available in {https://github.com/LauraFreiG/Covariates_selection.git}. (pdf 318KB)
Appendices
Appendix A: Simulation details for considered competitors
In this appendix, we remind the scenario A structure of the FLCM algorithm implemented in Ghosal and Maity (2022a) in Section A.1. Besides, the form of scenario (B) for the ANFCM testing performance introduced in Kim et al. (2018) is reviewed in Section A.2. Moreover, we explain how these algorithms are implemented in the simulation study of Sect. 4.3.
Code for simulations and real datasets analysis is available in the public GitHub repository https://github.com/LauraFreiG/Covariates_selection.git. In particular, this is summarized in the folder “Synchronous FCM”, inside the folder “Functional Concurrent Model”.
1.1 A.1 Implementation details for FLCM algorithm
Under the linear assumption, data for \(i=1,\dots ,n\) are generated as
where \(\beta _0(t)=1+2t+t^2\) and \(\beta _1(t)=d\cdot t/8\), for \(d\ge 0\). The original covariate samples \(X_i(\cdot )\) are i.i.d. copies of \(X(\cdot )\), where \(X(t)=a+b \sqrt{2}\sin (\pi t)+ c \sqrt{2}\cos (\pi t)\), with \(a\sim N(0,1)\), \(b\sim N(0,0.85^2)\) and \(c\sim N(0,0.70^2)\) independent. It is assumed that the covariate \(X_i(t)\) is observed with error, i.e., \(W_i(t)=X_i(t)+\delta _{it}\) is getting instead, where \(\delta _{it}\sim N(0,0.6^2)\) and changes with every i and t. The error process is considered as
where  ,
,  and
and  , with \(\xi _{i3t}\) being generated as a multivariate normal of dimension \(\mathcal {T}\) and these values change with i and t.
, with \(\xi _{i3t}\) being generated as a multivariate normal of dimension \(\mathcal {T}\) and these values change with i and t.
We consider the dense design, taking a total of \(\mathcal {T}=81\) equidistant time points in [0, 1], being \(t_1=0\) and \(t_{81}=1\). A Monte Carlo study is carried out using \(M=1000\) replicates to measure calibration and power, and p-values are calculated using \(B=100000\) samples generated under the null hypothesis of no effect (\(H_0: \beta _1(t)=0\) for all t). Following the authors’ guidelines, the number of basis components considered is \(Q=7\). To measure calibration and power we consider \(d=0\) and \(d=3,7\), respectively. Besides, we take \(n=60,100\) to compare their results with the MDD-based test ones. To implement this algorithm, we have used the public code which can be found in 10.1016/j.ecosta.2021. 05.003. In particular, we generate the data and use the FLCM.test1 function of the test.R script to implement the test.
1.2 A.2 Implementation details for ANFCM algorithm
In the case of the ANFCM approach, we perform Algorithm 1 of Kim et al. (2018) in hypothesis testing, which translates into testing the nullity of the second additive effect by
In this scenario, samples are generated verifying the additive assumption of
where \(F_0(t)=2t+t^2\) and \(F_1(X_{1i}(t),t)=d\{2\cos (X_1(t)t)\}\) for \(d\ge 0\). The covariate \(X_1(t)\) is given by \(X_1(t)=a_{0}+a_{1}\sqrt{2}\sin (\pi t)+a_{2}\sqrt{2}\cos (\pi t)\), where \(a_{0}\sim N\left( 0, \{2^{-0.5}\}^2 \right) \), \(a_{j1}\sim N\left( 0, \{0.85\times 2^{-0.5}\}^2 \right) \) and \(a_{2}\sim N\left( 0, \{0.7\times 2^{-0.5}\}^2 \right) \). However, it is assumed that this covariate is observed with error. In particular, we get \(W_{1i}=X_{1i}(t)+\delta _{it}\) where \(\delta _{it}\sim N(0,0.6^2)\) varies with respect to i and t. The considered error process is
where  ,
,  and
and  , being \(\xi _{i3t}\) generated as a multivariate normal of dimension \(\mathcal {T}\). All these values are simulated changing with i and t.
, being \(\xi _{i3t}\) generated as a multivariate normal of dimension \(\mathcal {T}\). All these values are simulated changing with i and t.
Here, the dense design scenario is considered with \(\mathcal {T}=81\) equidistant time points in [0, 1], being \(t_1=0\) and \(t_{81}=1\). To study its calibration and power behavior a Monte Carlo study is carried out. We employ a total of \(M=1000\) replicates to study both. In this case, p-values are calculated by means of \(B=200\) bootstrap samples in all cases. Besides, following Kim et al. (2018) parameters selection, the number of the basis components taken is \(Q=7\). In order to measure calibration and power we test with \(d=0\) and \(d=3,7\), we simulate under null and alternative hypotheses, respectively. Besides, we take \(n=60,100\) to compare their results with the MDD-based test ones. We have found the code available in https://www4.stat.ncsu.edu/~maity/software.html and we borrowed it to reproduce the ANFCM simulations. Specifically, we make use of the anova.datagen function of the datagenALL.RFootnote 2 script to generate the data and apply test.anova function of the test.R script to implement the algorithm, using now  .
.
Appendix B: Graphics
Histograms of the test statistics p-values under \(H_0\) for the FLCM (left column) and MDD (right column) methods in scenario A of Ghosal and Maity (2022a)
Histograms of the test statistics p-values under \(H_0\) for the ANFCM (left column) and MDD (right column) methods in modified scenario B of Kim et al. (2018)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Freijeiro-González, L., Febrero-Bande, M. & González-Manteiga, W. Novel specification tests for synchronous additive concurrent model formulation based on martingale difference divergence. TEST 32, 908–941 (2023). https://doi.org/10.1007/s11749-023-00857-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11749-023-00857-y
Keywords
- Covariates selection
- Functional concurrent model
- Martingale difference divergence (MDD)
- Significance tests










 ), midwest (
), midwest ( ), south (
), south ( ) and west (
) and west ( )
)
 function, we have changed
function, we have changed  for the expression
for the expression  to correct a typo. Besides, it is needed to change
to correct a typo. Besides, it is needed to change  by
by 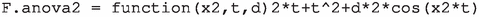 as well as
as well as  by
by  in function
in function 


