Density estimation for spatial-temporal models

Abstract

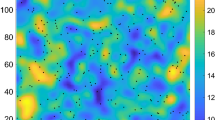
In this paper a k-nearest neighbor type estimator of the marginal density function for a random field which evolves with time is considered. Considering dependence, the consistency and asymptotic distribution are studied for the stationary and nonstationary cases. In particular, the parametric rate of convergence $\sqrt{T}$ is proven when the random field is stationary. The performance of the estimator is shown by applying our procedure to a real data example.

Appendices

Appendix A: Auxiliary results

Theorem 4

(Doukhan and Neumann 2006)

Suppose that X ₁,X ₂,…,X _T are real-valued random variables defined on a probability space $(\varOmega, \mathcal{A}, P)$ with $\mathbb {E} (X_{t} )=0$ and P(|X _t |≤M)=1, for all t=1,…,T and some M<∞. Let $S_{T} = \sum_{t=1}^{T} X_{t}$ and ϕ:ℕ²→ℝ⁺ be one of the following functions:

• ϕ(u,v)=2v;

• ϕ(u,v)=u+v;

• ϕ(u,v)=uv;

• ϕ(u,v)=ρ(u+v)+(1−ρ)uv, for some ρ∈(0,1).

We assume that there exist constants K,L ₁,L ₂<∞,μ≥0 and a nonincreasing sequence of real coefficients {α(n)} _n≥1 such that, for all u-tuples (t ₁,…,t _u ) and all v-tuples (l ₁,…,l _v ) with 1≤t ₁≤t _u <t _u +r=l ₁≤l _v ≤∞ the following inequality is fulfilled:

$$\bigl \vert \operatorname{cov} (X_{t_1} \cdots X_{t_u},X_{l_1} \cdots X_{l_v} )\bigr \vert \le K^2 M^{u+v-2} \phi(u,v)\alpha(r), $$

where

$$\sum_{j=0}^{\infty}(j+1)^k \alpha(j) \le L_1 L_2^k (k!)^\mu, \quad\forall k \ge0. $$

Then,

$$P (S_T \ge\epsilon ) \le\exp \biggl(-\frac{\epsilon^2/2}{\varSigma_T + \varGamma_T^{1/(\mu+2)}\epsilon^{(2\mu+3)/(\mu +2)}} \biggr), $$

where Σ _T can be chosen as any number greater than or equal to $\sigma_{T}^{2}=\operatorname{var} (S_{T} )$ and

$$\varGamma_T = 2 (K \vee M) L_2 \biggl( \biggl( \frac{2^{4+\mu} T K^2 L_1}{\varSigma_T} \biggr)\vee 1 \biggr). $$

Theorem 5

(Doukhan et al. 1984)

Let X ₁,X ₂,…,X _T be a sequence of α-mixing random variables verifying $\mathbb{E} (X_{t} )=0$ and |X _t |≤1, for all t=1,…,T. Let $S_{T} = \sum_{t=1}^{T} X_{t}$ and denote γ=2/(1−θ) and $\sigma= \sup_{1\le t \le T}\{\mathbb{E} (|X_{t}|^{\gamma } )^{1/\gamma}\}$. Then, there exist constants C ₁ and C ₂ which depend only on the mixing coefficients, such that for 0<θ<1,

$$P (S_T \ge\epsilon ) \le C_1 \frac{1}{\theta}\exp \biggl(-\frac {C_{2,T} \epsilon^{1/2}}{T^{1/4}\sigma^{1/2}} \biggr), $$

where C _2,T =C ₂ if T ^1/2 σ≤1 and C _2,T =C ₂ T ^1/4 σ ^1/2 if T ^1/2 σ>1.

Theorem 6

(Robinson 1983)

Let $\{V_{tT}\}_{t=1}^{T}$ be a triangular array of zero mean random variables and {b _T } _T≥1 a sequence of positive constants such that:

• (i) for each T, V _tT , t=1,…,T are identically distributed and α-mixing with the mixing coefficients α(r) verifying

  $$N \sum_{r=N}^{\infty} \alpha(r) \to0 \quad \textit{as } N \to \infty; $$

• (ii) there exists M>0 such that P(|V _tT |≤M)=1 for all t=1,…,T;

• (iii) b _T →0 and Tb _T →∞ as T→∞;

• (iv) there exists σ ²>0 such that $\mathbb{E} (V_{tT}^{2} )/b_{T} \to\sigma^{2}$ as T→∞;

• (v) $\mathbb{E} (\vert V_{tT} V_{(t+s)T}\vert ) \le C b_{T}^{2}$ for s≥1, t=1,…,T where C is independent of T.

Then

$$\frac{1}{\sqrt{Tb_T}}\sum_{t=1}^T V_{tT} \to\mathcal{N} \bigl(0, \sigma^2 \bigr) \quad \textit{in distribution.} $$

Appendix B: Proof of main results

Proof of Theorem 1

Let x∈ℝ be fixed. By definition of complete convergence we need to show that for all ϵ>0,

$$\sum_{T=1}^{\infty} P \bigl(v_T \bigl \vert \widehat{f}_{\mathcal {X}}(x)-f_{\mathcal{X}}(x)\bigr \vert > \epsilon \bigr) < \infty. $$

Using the definition of the estimator $\widehat{f}_{\mathcal{X}}(x)$, it is enough to prove that

$$ \sum_{T=1}^{\infty}P(A_T) < \infty\quad\mbox{and} \quad\sum_{T=1}^{\infty}P(B_T) < \infty, $$

(6)

where for $\epsilon_{T} \doteq\frac{\epsilon}{v_{T}}$, the sets A _T and B _T are defined by

$$A_T=A_T(x)\doteq \biggl\{h^{\mathcal{X}}_T(x)< \frac{k_T}{2T|\mathbf {S}|(f_{\mathcal{X} }(x)+\epsilon_T)} \biggr\} $$

and

$$B_T=B_T(x)\doteq \left \{ \begin{array}{l@{\quad}l} \{h^{\mathcal{X}}_T(x)>\frac{k_T}{2T| {\mathbf{S} }|(f_{\mathcal{X}}(x)-\epsilon_T)} \}&\mbox{si } f_{\mathcal{X}}(x)>\epsilon_T \\ {\emptyset} & \mbox{si } f_{\mathcal{X}}(x)\le\epsilon_T. \end{array} \right . $$

To prove the left-side inequality of (6) (the proof of the right-side inequality is identical and it will be omitted), let us define $a_{T}=a_{T}(x) \doteq\frac{k_{T}}{2T|{\mathbf {S}}|(f_{\mathcal{X} }(x)+\epsilon_{T})}$ so that $A_{T} = \{h^{\mathcal{X}}_{T} < a_{T} \}$. From the equivalence

$$h^{\mathcal{X}}_T < a_T \Leftrightarrow\sum _{t=1}^T \underbrace {\int_{\mathbf{S}} \mathbb{I}_{(x-a_T,x+a_T)} \bigl(\mathcal{X}_t({\mathbf{s}})\bigr)\,d \mathbf {s}}_{\doteq Y_{Tt}} >k_T, $$

we have

$$ P (A_T ) = P \Biggl(\sum_{t=1}^T Y_{Tt}> k_T \Biggr). $$

(7)

Next we define $\overline{Y}_{Tt}\doteq Y_{Tt}-\mathbb{E} (Y_{Tt} )$ and the probability $p_{T} \doteq P(\mathcal{X}_{t}({\mathbf{s}}) \in(x-a_{T}, x+a_{T}))$. Since $\mathbb{E} (Y_{Tt} ) = |\mathbf{S}| p_{T}$, using the definition of a _T we get

(8)

By the Mean Value Theorem there exists x _T ∈(x−a _T ,x+a _T ) for which $\frac{p_{T}}{2a_{T}}=f_{\mathcal{X}}(x_{T})$. In addition, by condition H2, the definition of a _T and the fact that ϵ _T →0 we have

$$\biggl \vert \frac{p_T}{2a_T}-f_{\mathcal{X}}(x)\biggr \vert = \bigl \vert f_{\mathcal{X}}(x_T)-f_{\mathcal{X} }(x)\bigr \vert \leq K |x_T-x| \leq K {a_T} \le\frac{\epsilon_T}{2}, $$

from which it follows that $\frac{p_{T}}{2a_{T}} \le f_{\mathcal{X}}(x) + \frac {\epsilon_{T}}{2}$ and then

$$1-\frac{1}{f_{\mathcal{X}}(x)+\epsilon_T} \frac{p_T}{2a_T} \ge\frac{\epsilon_T/2}{f_{\mathcal{X}}(x)+\epsilon_T} \ge C(x,\epsilon ) \frac{1}{v_T}. $$

Therefore, with this inequality in (8) we get

$$ P(A_T) \le P \Biggl( \sum _{t=1}^T \overline{Y}_{Tt}> C \frac {k_T}{v_T} \Biggr). $$

(9)

(a) Weakly dependent case: in order to use a Bernstein type inequality in (9), we need the following Lemma which will be proved in Appendix B.

Lemma 4

Under H3 for $\mathcal{X}({\mathbf{s}})$ we have

• (i) for any u-tuple (t ₁,…,t _u ) and any v-tuple (l ₁,…,l _v ), 1≤t ₁≤t _u <t _u +r=l ₁≤l _v ≤T we have

  $$\bigl \vert \operatorname{cov} (\overline{Y}_{Tt_1} \cdots \overline{Y}_{Tt_u},\overline{Y}_{Tl_1} \cdots \overline {Y}_{Tl_v} )\bigr \vert \le \bigl(2|\mathbf{S}| \bigr)^{u+v} \phi(u,v) \alpha(r), $$

  where 2|S| is such that $\vert \overline {Y}_{Tt}\vert \le2|\mathbf{S}|$ for all t, α(r)→0 with ϕ any of the functions given in H3;

• (ii) for some constant C,

  $$\operatorname{var} \Biggl(\sum_{t=1}^T \overline{Y}_{Tt} \Biggr) \le C T. $$

Therefore, Lemma 4(i) implies that the sequence $\{\overline{Y}_{Tt} \}_{t=1}^{T}$ is $(\mathcal{G},\alpha ,\psi)$-weakly with f:ℝ^u→ℝ and g:ℝ^v→ℝ given by $f(\overline{Y}_{Tt_{1}}, \ldots, \overline{Y}_{Tt_{u}})= \overline{Y}_{Tt_{1}} \cdots \overline{Y}_{Tt_{u}}$ and $g(\overline{Y}_{Tl_{1}}, \ldots, \overline{Y}_{Tl_{v}})= \overline{Y}_{Tl_{1}} \ldots\overline{Y}_{Tl_{v}}$, respectively, and $\psi: \mathcal{G}^{2} \times \mathbb{N}^{2} \to\mathbb{R}^{+}$ defined by ψ(f,g,u,v)=(2|S|)^u+v ϕ(u,v) with ϕ any of the four functions given in H3. Therefore, applying Theorem 4 with K=(2|S|)², M=2|S|, Γ _T =C and Σ _T =CT in (9) we have

and the result follows since (2μ+3)/(μ+2)<2 and H4 $(\frac{v_{T}}{k_{T}})^{2} T \to0$ and, as a consequence, $\frac {v_{T}}{k_{T}}\to0$.

(b) α-mixing case: under H1, H2, H3′ and H4′ for $\mathcal{X} ({\mathbf{s}})$. Since $\mathcal{X}_{t}$ verifies H5, $\overline{Y}_{Tt}$ inherits the same condition and then we apply the Bernstein inequality given in Theorem 5 to the random variables $Z_{Tt}\doteq\frac{\overline{Y}_{tT}}{2|\mathbf{S}|}$ with |Z _Tt |≤1 and $\mathbb{E} (Z_{Tt} ) = 0$. For $\gamma= \frac {2}{1-\theta}$ with 0<θ<1, it is easy to verify that $\mathbb{E} (|Z_{Tt}|^{\gamma} )^{1/\gamma} \le (2|\mathbf{S}|)^{1-\gamma}$ so that σ≤(2|S|)^1−γ and then, since $\frac {C_{2,T}}{T^{1/4}\sigma^{1/2}} \ge C$ in (9) we have

$$ \sum_{T=1}^{\infty}P(A_T) \le T_0 + C \frac{1}{\theta}\sum_{T=T_0}^{\infty} \exp \biggl(- C\sqrt{\frac{k_T}{v_T}} \biggr), $$

which is finite by H4′.  □

Proof of Theorem 2

For a fixed x∈ℝ we define

$$S_T = \sum_{t=1}^T Y_{Tt}, \quad s_T^2 = \operatorname {var} (S_T ) \quad\mbox{and}\quad a_T = \frac{k_T}{2T|\mathbf {S}|(f_{\mathcal{X} }(x)+\frac{z}{\sqrt{T}})}. $$

From the definition of $\widehat{f}_{\mathcal{X}}(x)$ and analogously to (7) we have

Then the proof will be completed if we prove:

• (a) $\frac{S_{T} - \mathbb{E} (S_{T} )}{s_{T}} \to\mathcal{N} (0, 1 )$ in distribution;

• (b) $\frac{k_{T} - T|\mathbf{S}|p_{T}}{s_{T}} \to \frac {2|\mathbf{S}|}{c_{o}}z$.

(a) It will a consequence of $\frac{S_{T} - \mathbb {E} (S_{T} )}{\sqrt{T} a_{T} } = \frac{1}{\sqrt{T} a_{T} }\sum_{t=1}^{T} \overline{Y}_{tT} \to\mathcal{N} (0, c_{0}^{2} )$ and $\frac {s_{T}^{2} }{T a_{T}^{2}} \to c_{0}^{2}$ where $c_{0}^{2}$ is given in H6. To prove the second part observe that

Then,

$$ \frac{s_T^2}{T a_T^2} = \frac{1}{T a_T^2} \sum _{t=1}^T \operatorname {var} (Y_{Tt} ) + 2 \frac{1}{T a_T^2} \sum_{t=1}^{T-1} \sum _{l=1}^{T-t} \operatorname{cov} (Y_{Tt}, Y_{Tl+l} ) \doteq I +\mathit{II}. $$

(10)

Since a _T ∼k _T /T, from H6 we get

(11)

from which follows that $I \to c_{0}^{2}$ as T→∞. On the other hand, for N integer we write,

$$|\mathit{II}| \le2 \frac{1}{T a_T^2} \sum_{t=1}^{T-1} \sum_{l=1}^{N-1} \big|\operatorname{cov} (Y_{Tt}, Y_{Tt+l} )\big| \hspace{-1pt}+\hspace{-1pt} 2 \frac{1}{T a_T^2} \sum _{t=1}^{T-1} \sum_{l=N}^{T-t} \big|\operatorname{cov} (Y_{Tt}, Y_{Tt+l} )\big| \hspace{-1pt}\doteq \hspace{-1pt}\mathit{III} \hspace{-1pt}+\hspace{-1pt} \mathit{IV}, $$

where the term IV is considered zero if T−t<N. Since

$$\operatorname{cov} (Y_{Tt}, Y_{Tl+l} ) = \int _{\mathbf {S}} \int_{\mathbf{S}} \bigl(P \bigl(A_t({\mathbf{s}}) \cap A_{t+l}(\mathbf{r})\bigr) - P \bigl(A_t(\mathbf{r})\bigr) P\bigl(A_{t+l}(\mathbf{r})\bigr) \bigr) \,d\mathbf{s}\,d\mathbf{r}, $$

and $A_{t}({\mathbf{s}}) \doteq\{\mathcal{X}_{t}({\mathbf{s}}) \in (x-a_{T},x+a_{T})\} \in\mathcal{M}_{t}^{t}$ and $A_{t+l}(\mathbf{r}) \doteq \{\mathcal{X}_{t+l}({\mathbf{s}}) \in(x-a_{T}, x+a_{T})\} \in\mathcal{M}_{t+l}^{t+l}$ for each fixed s and r, hypothesis H5 implies that

from which follows

$$\mathit{IV} \le\frac{C}{T a_T^2} \sum_{t=1}^{T-1} \sum_{l=N}^{T-t} \alpha (l) \le \frac{C}{ a_T^2} \sum_{l=N}^{\infty} \alpha(l) = \frac {C}{ N a_T^2} N \sum_{l=N}^{\infty} \alpha(l). $$

On the other hand, from H7 we have

(12)

for some constant C which implies that $\mathit{III} \le2C N a_{T}^{2}$ and hence

$$|\mathit{II}| \le2C N a_T^2 + \frac{C}{ N a_T^2} N \sum _{l=N}^{\infty} \alpha(l). $$

Let ϵ>0 fixed and $N = \lfloor\frac{\epsilon }{a_{T}^{2}} \rfloor$. For this choice we get $|\mathit{II}| \le C \epsilon+ \frac{C}{\epsilon} N \sum_{l=N}^{\infty} \alpha(l)$ for T large enough (since $a_{T} \sim \frac{k_{T}}{T} \to0$). From hypothesis H5 there exists N ₀ such that if M≥N ₀, $M \sum_{l=M}^{\infty} \alpha(l) < \epsilon^{2}$. On the other hand, again since a _T →0, there exists T ₀ such that if T≥T ₀, $\lfloor \frac {\epsilon}{a_{T}^{2}} \rfloor \ge N_{0}$ and then $\lfloor \frac{\epsilon}{a_{T}^{2}} \rfloor \sum_{l=\lfloor\frac{\epsilon}{a_{T}^{2}}\rfloor}^{\infty} \alpha(l) < \frac{\epsilon^{2}}{2}$ which implies that II≤Cϵ which implies

$$ \frac{s_T^2}{T a_T^2} \to c_0^2. $$

(13)

To prove that $\frac{S_{T} - \mathbb{E} (S_{T} )}{\sqrt{T} a_{T} } = \frac{1}{\sqrt{T} a_{T} }\sum_{t=1}^{T} \overline{Y}_{tT} \to \mathcal{N} (0, c_{0}^{2} )$ we will show that the variables $V_{Tt} \doteq\overline{Y}_{tT}$ verify the assumptions (i)–(v) of the Lindeberg version of the CLT given in Theorem 6 with $b_{T} = a_{T}^{2}$. As before, since $\mathcal{X}_{t}$ verifies H5, $\overline {Y}_{Tt}$ inherits the same condition from which (i) follows. Condition (ii) holds for M=2|S|. (iii) follows from (4) (since k _T →∞ and $a_{T} \sim\frac{k_{T}}{T} \to0$), H5 implies (iv) (see (11)) and H7 implies (v) (see (12)). Therefore, from Theorem 6 we get the result since $\sigma^{2} = c^{2}_{0}$.

To prove (b) we use the definition of a _T to get

(14)

By Taylor Theorem and since f has two derivatives bounded, for x ^∗ between x and u we have

$$ \biggl \vert \int_{x-a_T}^{x+a_T}\bigl(f_{\mathcal{X}}(x)-f_{\mathcal {X}}(u) \bigr) \,du\biggr \vert = \biggl \vert -\frac{1}{2}\int _{x-a_T}^{x+a_T}f_{\mathcal{X}}'' \bigl(x^*\bigr) (u-x)^2\, du\biggr \vert \le C s_T^{-1} T a_T^3. $$

Therefore, in (14) we have

$$\frac{k_T -T|\mathbf{S}|p_T}{s_T} = O\bigl(s_T^{-1} T a_T^3\bigr)+ \frac{2 |\mathbf{S}| z}{s_T/\sqrt{T} a_T}. $$

Finally, by hypothesis (4) and (13) $s_{T}^{-1} T a_{T}^{3} \rightarrow0$ then from (11) we get (b). □

Proof of Theorem 3

This proof will be an immediate consequence of Theorem 1 and of the following lemma which was proved in Llop et al. (2011, Lemma 5, p. 85). □

Lemma 5

Assume H1–H3 and choose two sequences {k _T } and {v _T } of positive real numbers converging to infinity such that, for each fixed s, $v_{T} (T/k_{T})|\bar{e}_{T}({\mathbf{s}})| \rightarrow0$ a.co. For this sequences, suppose that H4 hold. Then for each x∈ℝ

$$\lim_{n \rightarrow\infty} v_T \bigl(\widehat{f}_u\bigl(x- \bar{\mathcal {X}}_T({\mathbf{s}})\bigr)- \widehat{f}_e \bigl(x-\mu({\mathbf{s}})\bigr) \bigr)=0, \quad \textit{a.co.} $$

where $\widehat{f}_{e}$ is the estimator of f _e .

Appendix C: Proof of the auxiliary lemmas

Proof of Lemma 2

We need to prove that if α(r)≤aρ ^r with 0<ρ<1 and a>0 then, $\sum_{j=0}^{\infty}(j+1)^{k} \alpha(j) \le L_{1} L_{2}^{k} (k!)^{\mu}, \forall k \ge0$. For that, let us suppose that α(r)≤aρ ^r for some 0<ρ<1 and a>0. If f ^(k) denotes the kth derivative of f then

(15)

Let C(k,j) be denote the combinatorial number . Since

we have

where in the last equality we have used the Binomial Theorem. Then, with this inequality in (15), we get

$$\sum_{j=0}^{\infty} (j+1)^k \alpha(j) \le\frac{a}{1-\rho} \biggl(\frac{1}{1-\rho} \biggr)^k k! $$

Therefore, taking $L_{1} = \frac{a}{1-\rho}$, $L_{2}=\frac{1}{1-\rho}$ and μ=1 we get the result. □

Proof of Lemma 3

For T and x fixed, the function

$$G(r)\doteq\frac{1}{T}\sum_{t=1}^T \int_{I_{(x,r)}} l_T(u,\mathcal{X}_t)\,du, $$

is strictly increasing with G(0)=0. On the other hand, due to the existence of local time we can write

$$G(r) = \frac{1}{T} \sum_{t=1}^T \lambda(I_{(x,r)},\mathcal{X}_t), $$

then, G(r)→|S| when r→∞ and therefore, the existence and uniqueness of $h^{\mathcal{X}}_{T}(x)$ is ensured. For a further reading on local times see Geman and Horowitz (1980). □

Proof of Lemma 4

To prove part (i) let us consider the u-tuple (t ₁,…,t _u ) and the v-tuple (l ₁,…,l _v ) for 1≤t ₁≤t _u <t _u +r=l ₁≤l _v ≤T and let C(k,j) be denote the combinatorial number . Since $\mathbb{E} (Y_{Tt} )= |\mathbf{S}| p_{T}$ then,

Therefore, taking absolute value and considering that |p _T |≤1 we get

(16)

To compute

$$\Biggl \vert \operatorname{cov} \Biggl(\prod_{i=1}^{k} Y_{Tt_i},\prod_{j=1}^{m} Y_{Tl_j} \Biggr)\Biggr \vert = \Biggl \vert \mathbb{E} \Biggl(\prod _{i=1}^{k} Y_{Tt_i} \prod _{j=1}^{m} Y_{Tl_j} \Biggr) - \mathbb{E} \Biggl(\prod_{i=1}^{k} Y_{Tt_i} \Biggr)\mathbb{E} \Biggl(\prod_{j=1}^{m} Y_{Tl_j} \Biggr)\Biggr \vert , $$

we will consider the following events:

$$A_{t_i}({\mathbf{s}}) \doteq \bigl\{\omega\in\varOmega: \mathcal{X}_{t_i}({\mathbf{s}},\omega) \in(x-a_T,x+a_T) \bigr\}, \quad i = 1,\ldots,u $$

and

$$A_{l_j}(\mathbf{r}) \doteq \bigl\{\omega\in\varOmega: \mathcal {X}_{l_j}(\mathbf{r} ,\omega) \in(x-a_T,x+a_T) \bigr\}, \quad j = 1,\ldots,v. $$

In addition, we will denote

$$\int_{\mathbf{S}^u} \, d\mathbf{s}^u \doteq\int _{\mathbf {S}}\cdots\int_{\mathbf{S} } \, d \mathbf{s}_1 \cdots d\mathbf{s}_u. $$

Then,

(17)

and similarly

$$\mathbb{E} \Biggl(\prod_{i=1}^{k} Y_{Tt_i} \Biggr)\mathbb{E} \Biggl(\prod_{j=1}^{m} Y_{Tl_j} \Biggr) = \int_{\mathbf{S}^u}\int _{\mathbf{S}^v} P \Biggl(\bigcap_{i=1}^{k} A_{t_i}({\mathbf {s}}) \Biggr) P \Biggl(\bigcap _{j=1}^{m} A_{l_j}(\mathbf{r}) \Biggr) \,d \mathbf{s}^u \,d\mathbf{r}^v. \nonumber $$

Hence,

(18)

where in the last inequality we have used hypothesis H4 since, for each fixed s,r, since k≤u and m≤v,

$$\bigcap_{i=1}^{k} A_{t_i}({ \mathbf{s}}) \in\mathcal{M}_{t_1}^{t_u} \quad\mbox{and} \quad \bigcap_{j=1}^{m} A_{l_j}(\mathbf {r}) \in \mathcal{M}_{l_1}^{l_v}, $$

with 1≤t ₁≤t _u <t _u +r=l ₁≤l _v ≤T. Finally, with inequality (18) in (16) we get

To prove part (ii) of this lemma, first observe that since $\operatorname{var} (Y_{Tt} ) \le\mathbb{E} (Y_{Tt}^{2} ) \le|\mathbf{S}|^{2} p_{T}^{2} \le|\mathbf{S}|^{2}$ we may write

 □