Abstract
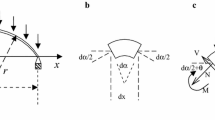
On the basis of the Kármán-Donnell theory of thin shells with large deflections and the Boltzmann laws for linear viscoelastic materials, the mathematical model for viscoelastic open shallow shells was formulated. By using the Galerkin average method, the original integro-partial-differential dynamic system was simplified as a integro-ordinary-differential dynamic system, which can be transformed into a ordinary differential dynamic system by introducing new variables. The dynamical behavior was studied by some classical methods. Dynamical properties, such as, chaos, strange attractor, limit cycle etc., were discovered.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Potapov V. D., Stability of compressed viscoelastic orthotropic shells, J. Appl. Mech. and Tech. Phy., 1978, 18:586–592
Ding Rui, The Dynamical Analysis of Viscoelastic Structures, Ph. D. Thesis, Lanzhou, Lanzhou University, 1997
Cheng Changjun, Zhang Nenghui, Variational principles on static-dynamic analysis of viscoelastic thin plates with applications, Int. J. Solids Struct., 1998, 35:4491–4505
Zhang Nenghui, Cheng Changjun, Non-linear mathematical model of viscoelastic thin plates with applications, Comput. Methods Appl. Mech. Engng., 1998, 165:307–319
Cheng Changjun, Zhang Nenghui, Chaotic and hyper-chaotic behavior of viscoelastic rectangular plates, Ada Mechanica Sinica, 1998, 30:690–699 (in Chinese)
Cheng Changjun, Zhu Zhengyou, Buckling and Bifurcation in Structures, Lanzhou, Lanzhou University Press, 1991 (in Chinese)
Xu Zhilun, The Theory of Elasticity, Beijing, High Education Press, 1988 (in Chinese)
Shimada I. Nagashima T., A numerical approach to ergodic problem of dissipative systems, Progr. Theor. Phys., 1979, 61:1605–1615
Kubicek M. and Marek M., Computational Methods in Bifurcation Theory and Dissipative Structures, New York, Springer-Verlag, 1983
Author information
Authors and Affiliations
Additional information
Supported by the Development Foundation of Shanghai Municipal Commission of Education (99A01)
About this article
Cite this article
Zhang, Nh., Cheng, Cj. Dynamic properties of viscoelastic open shallow shells. J. of Shanghai Univ. 4, 279–283 (2000). https://doi.org/10.1007/s11741-000-0041-x
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s11741-000-0041-x