Abstract
In order to decrease mass, and thus fulfil the targets for airplane traffic emission reduction, the amount of titanium alloys used for structural components is rising. With the conventional milling process, low material utilization and short tool life lead to high manufacturing costs. Therefore, a process chain consisting of wire and arc additive manufacturing (WAAM) and machining is developed. To realize its full potential, the machining process needs to be adapted to the near-net shaped components. A special focus lies on the machining allowance, since it influences both processes and in result the final part quality. In this paper a method to model the machining allowance is proposed and verified by analysing the changes from waviness to surface roughness occurring during peripheral milling of WAAM parts.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Motivation
The European Commission’s objective to reduce the amount of nitrogen oxides (NOx) and carbon dioxide (CO\(_{2}\)) per kilometer flown leads to a need to lower the fuel consumption of airplanes considerably [1]. Reduced airplane weight helps to achieve this goal, which in turn compels the increasing use of lightweight titanium alloys such as Ti-6Al-4V [2]. The conventional machining for airplane structural components made from Ti-6Al-4V is mainly done by milling from slab.
The ratio of the raw materials’ weight to the weight of the material used in the aircraft is called the Buy-to-Fly (BTF)-ratio. For structural components this ratio, depending on the part, can approach 37, when a conventional milling process is used [3]. Due to the contamination of the chips with cooling lubricants, this leads to a large amount of material waste [4] and, since Ti-6Al-4V is a difficult to machine material [5], to high manufacturing costs.
In order to reduce the production costs for these parts, a process chain, which consists of additive manufacturing and machining, was developed. Since the machine tools for conventional machining already are present in most manufacturing companies, a sequential setup on two machines, one for additive manufacturing and one for machining, was preferred over one specialized hybrid machine tool. For the additive manufacturing process wire and arc additive manufacturing (WAAM) was selected, because this process allows the production of structural components with large outer dimensions [6].
To ensure that the final part quality is met, the minimum amount of material needed to be removed from the near-net shaped part has to be determined. Otherwise, not or not-sufficiently machined surfaces remain on the final part. For casting and forging processes in combination with machining, this additional material, which allows the achievement of the desired surface and dimensional accuracy, is defined as the machining allowance (MA) [7, 8]. It is chosen according to the outer dimensions of the cast or forged part. Factors to be considered for the design of cast parts are the shrinkage of the material, surface impurities, warpage and surface variations [7].
Some research has been carried out on the milling of additively manufactured parts [9,10,11], proving the process chain’s capability for the manufacture of high quality parts. As was experimentally determined by Frank et al. [12], a high surface quality could be achieved with a machining allowance of 1.25 mm while milling titanium parts manufactured by electron beam melting. Li et al. [13] developed a regression model for the surface roughness Ra depending on the welding and cutting parameters for the fabrication of wire and arc manufactured aluminum parts. The authors found the resulting surface roughness to be dependent on the spindle speed, the feed rate and the depth of cut.
Several sources state a machining allowance having to be added to the workpiece for the machining of additively manufactured parts [14,15,16]. However, the research into the sizing of this machining allowance is limited.
A method to determine the machining allowance for parts manufactured by electron beam melting was developed by Manogharan et al. [10]. The authors analyzed the maximum deviation in their setup—the positioning in the machine tool—and calculated a machining allowance based on this deviation.
For parts manufactured by laser beam melting a method to determine the machining allowance was proposed by Dietz [17]. As shown by the author, the MA has to be larger than the sum of three parameters: the manufacturing inaccuracies of the individual manufacturing processes, the amount of material having to be removed to achieve the desired surface finish and the positioning error in the machine tool.
In this paper, a model to determine the machining allowance for a process chain consisting of wire and arc additive manufacturing and machining is proposed. In order to validate the model, first, the surfaces characteristics of Ti-6Al-4V parts fabricated by WAAM were analyzed. Then, the WAAM parts were machined with a width of cut calculated by the model and the resulting surfaces were evaluated.
2 Introduction to the process chain
In order to reduce the production costs for Ti-6Al-4V structural components, a process chain which consists of WAAM and milling was developed.
In a first step, during production planning, a work plan sequence for the process chain is generated. The near-net shaped component to be manufactured by WAAM (the WAAM model) is also defined in this process step. This model differs from the workpiece model for example by the machining allowance and support structures. Next, the WAAM model is manufactured and heat treated. The result is a near-net shaped component (the WAAM part), which varies from the model for example due to heat induced distortion. Finally, the near-net shaped component is machined to final part specifications.
3 Modelling the minimum machining allowance
The main objective, especially for the manufacture of aircraft components, is to achieve process stability. This can be accomplished by ensuring the amount of material removed from the near-net shaped component is larger than the inaccuracies occurring during the process chain.
The imprecisions resulting from the WAAM process can be classified as deviations of the WAAM part from the ideal WAAM model.
At the same time, the transfer from one machine setup to another and the inaccuracies of the machining process also need to be compensated by the MA. This follows the logic of Dietz [17] who summarized all inaccuracies during the process chain and ensured that the machining allowance is larger than the sum of these inaccuracies.
In conclusion, the machining allowance MA is modelled as
where D1...n denote the deviations from the ideal WAAM part and Ei denote the machining errors.
3.1 Deviations of the WAAM part from the WAAM model
Several deviations of the WAAM part from the WAAM model can be found. For example, the high temperature gradient during the WAAM leads to residual stress which results in distortions [18], while the bead deposition and torch movement lead to a distinctive surface profile [9, 19].
In general, deviations from the ideal geometry are classified into the six categories listed in Table 1 [20, 21].
All of these should be taken into consideration for the calculation of the MA, since all might occur within the WAAM process [18, 22].
3.2 Machining errors
The machining errors are divided into two categories: those being specific for the process chain and those occurring during any milling process. The machine tool positioning accuracy for example should be considered for any milling process.
Process chain specific errors are for example the error due to the digitalization of the additively manufactured part for the milling tool path planning and the positioning error within the machine tool.
4 Characterization of WAAM part surfaces
In order to determine the deviations D1...6, it is necessary to methodically characterize the surfaces properties of WAAM parts and determine which welding parameters have the highest influence on the deviations from the ideal part. For this purpose, test specimens in the form of walls on a substrate plate were manufactured by WAAM with a variation of the factors wire feed rate and wall width. Subsequently, their surface properties were analyzed.
4.1 Method
Twelve test parts were manufactured by WAAM with the equipment at the iwb (Institute for Machine Tools and Industrial Management, TU Munich). The WAAM equipment consists of a CMT Advanced 4000 R welding torch (Fronius International GmbH) mounted on a 6-axis industrial robot KR15/2 (Kuka AG). For the welding the CMT mode was employed. The welding process was carried out on substrate plates of Ti-6Al-4V with a thickness of 6 mm, while using a Ti-6Al-4V welding wire with a diameter of 1.2 mm. To keep the oxidation to a minimum, the welding took place in argon atmosphere. As a result, the oxygen level was kept below 400 ppm. At the same time, He 4.6 was used as welding torch gas to keep the arc stable.
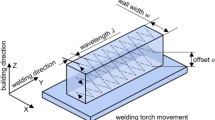
In Fig. 1 the path of the welding torch is illustrated. As depicted, the welding was carried out in a zigzag pattern. The wavelength of the torch \(\lambda _{T}\) was set to 4 mm, the offset between layers o\(_{_T}\) to 3 mm.
Six combinations of wire feed (X1) and wall width (X2) were manufactured twice in a full-factorial design, visible in Table 2. The feed rate of the welding torch was 1.2 m/min. The test parts have a length of 80 mm with ten layers each. Consequently, the test part heights varied due to the variation in wire feed rate.
After manufacture, the surfaces in Y-Z-direction of the test parts were captured on both sides using a 3D optical profiler VR-3100 (Keyence Corporation). The deviations D3-5 were then determined using the VR Analyzer VR-H2AD application (Keyence Corporation). The position deviation D6 was not assessed, since the test parts had no fixed position. Due to the torch movement, a waviness in Y-direction correlating to the wavelength \(\lambda _{T}\) and in Z-direction correlating to the offset between the layers o\(_{_T}\) was expected. Therefore, the filters were set to: \(\lambda _{S}\)= 50 µm, \(\lambda _{C}\) = 0.25 mm and \(\lambda _{F}\)= 8 mm [23]. For the \(\lambda _{S}\)-filter this is the smallest possible value, due to the limited measurement accuracy. At the same time, the maximum height of the surface Sz of the primary surface was measured without applying any filters [24].
4.2 Results
4.2.1 Influence of the wire feed rate
The influence of the wire feed rate and the wall width on the surface was examined by analyzing the maximum height of the surface Sz. For this purpose, the two parts per combination were each measured on both sides. Then, these measured Sz-values of each side and designation were averaged. The average is denoted as \(\overline{S_{z}}\). The results are shown in Table 3. The standard deviation \(\upsigma\) was calculated as well from the four values obtained for each combination.
Next, an analysis of variance (ANOVA) was carried out (Table 3). Sum Sq. denotes the sum of squares, df the degrees of freedom, Mean Sq. the mean squares and F the calculated value for the F-test. The F-value for X1 is much higher than the F-value for X2. Accordingly, the wire feed rate X1 has a significantly higher influence on the maximum height of the surface \(\overline{S_{z}}\) than the wall width X2.
At the same time, on test parts manufactured with a lower wire feed rate a higher amount of spatter could be detected, see Fig. 2.
4.2.2 Characterization of the surface roughness deviation D3 and the waviness deviation D4
For the deviations D3 and D4, corresponding to the surface roughness and the waviness respectively, the maximum profile heights Rz and Wz were measured according to DIN EN ISO 4287 [25]. The maximum profile height was chosen, because for the minimum machining allowance the maximum deviations need to be determined.
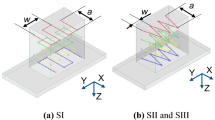
In Fig. 3 the method to characterize the surfaces is shown. In Y-direction a total of eleven profiles with a distance of 40 px was measured, whereas in Z-direction 21 profiles with a distance of 80 px were measured.
The resulting waviness profile W for one measurement of a part, both in Z- and Y-direction, with the factor combination F is displayed in Fig. 4. Both sides of each part were measured. In the figure they are shown as the +X-side and the -X-side.
In comparison to the waviness Wz, the results show a low arithmetical mean roughness Ra, which ranges between 0.001 mm and 0.013 mm for all parts. The maximum height Rz was not determined due to the measurement inaccuracy of the optical profiler. This roughness is attributed to the cooling of the melt, but since it is significantly smaller than the waviness, it is not significant for the calculation of the machining allowance.
On test parts with minimal or without spatter the waviness profile is distinctive and correlates to the welding torch path.
The waviness does not exceed 0.4 mm in Y-direction and the wavelength correlates to the wavelength \(\lambda _{T}\) of the torch movement. In Z-direction the waviness also does not exceed 0.4 mm and corresponds to two times the torch offset o\(_{_T}\), though the correlation is not as pronounced as in Y-direction. A probable reason for the correlation to twice the offset is the deposition of the layers from both directions (Fig. 1).
The same overall dependency between torch movement and surface profile was found for all test parts. However, with increased spatter the correlation is not as prominent.
In Fig. 5 the mean maximum waviness \(\overline{W_{z}}\) is shown. It is defined as the arithmetic mean of the maximum profile height Wz between the two sides of each test part. Each factor combination was manufactured twice, denoted as No. 1 and No. 2.
In general the waviness in Z-direction is higher than in Y-direction. Furthermore, the waviness decreases with increased wire feed rate. However, no trend could be detected due to the different wall widths. This is supported by the beforehand performed ANOVA (compare to Table 3), showing the dominant influence of the wire feed rate compared to the wall width.
4.2.3 Evaluation of the form deviation D5
According to DIN 4760 [20], deviations of form are those being observed on the whole surface of a geometric element or part. Generally, these include for example straightness, flatness and roundness [26]. The measurement of these variables is difficult due to the distinctive surface profile, shown in Fig.4.
Instead, two predominantly observable form deviations were found: spatter and distortion.
For the manufacture of WAAM parts a process parameter combination should be found resulting in zero spatter. Otherwise, if complex parts are manufactured, already solidified spatter might be remelted. This could result in microstructural changes. Therefore, spatter is not further discussed in this paper.
Distortion, on the other hand, is a form deviation that needs to be studied. The distorted part, which is manufactured during the WAAM process, has to exceed the dimensions of the part to be manufactured. Only then, all surfaces can be machined.
In order to measure the distortion of the substrate plate, the following method was developed (Fig. 6). A straight line is constructed between the points where the substrate plate and the welded material are connected at the outer corners of the part (P1 and P2). The distortion ds is then measured as the distance to a parallel line drawn through the lowest point on the substrate plate (P3).
When measuring the part from both sides (-X- and +X-direction), the measurements are expected to deviate only slightly. Unfortunately, this deviation in measurements between the both sides of one part was found to be up to 22 % of the measured value for the distortion ds. Therefore, the influence of the process parameters on the distortion could not be determined. However, with the parameters in use, the distortion did not exceed 1.00 mm. It is, therefore, smaller than the maximum surface and profile height (Sz, Wz) of the test parts.
4.3 Conclusion
The values for the waviness deviation D4 exceed both the values for surface roughness deviation D3 and form deviation D5. Following Eq. 1 for the modelling of the machining allowance, the minimum machining allowance should therefore be set to the value of D4, if machining errors are not considered.
With process parameters leading to spatter free deposition, the surface profile is distinctive and it is expected to be possible to predict the waviness and surface roughness based on the welding torch tool path.
5 Validation of the proposed model
The proposed model for the machining allowance (Eq. 1) was partially validated by peripheral milling of the test parts.
5.1 Method
According to Sect. 2, the largest deviation from the ideal part, which is the waviness deviation D4, should be used as the minimum machining allowance.
The waviness can be measured either with a profile-based method according to [25] or an area-based method [24]. As for the WAAM parts, not all test parts were spatter free. This leads to large inaccuracies while measuring with the profile-based method. The effect can be observed in Fig. 5 were the standard deviation of parts with a large amount of spatter (combination A and D) is high compared to those with a low amount of spatter (combination C and F). In comparison, the standard deviation of the \(\overline{\hbox {S}_{z}}\)-values is lower, see Table 3. So, instead of using the maximum profile height value Wz to determine the MA, the averaged maximum height of the surface \(\overline{S_{z}}\) was used. By removing an amount of material similar in depth to \(\overline{S_{z}}\), supposedly, a non-wavy, defect free surface can be achieved.
To verify this assumption, each wall was divided into six areas of cut. The maximum width of cut for each wall was set to 125 % the \(\overline{S_{z}}\)-value of its designation. The minimum width of cut was set to 0 % of the \(\overline{S_{z}}\)-value, in order to remove spatter from the surface. The remaining four areas were milled with 25, 50, 75 and 100 % of the \(\overline{S_{z}}\)-value. The peripheral milling was carried out on a G352T 5-axis universal machining center (GROB Werke GmbH & Co. KG) with the settings shown in Table 4. For the tool path planning scans of the parts were used as a reference.
After the milling process, the surface properties of the test parts were once again measured on the 3D optical profiler VR-3100 (Keyence Corporation).
5.2 Results and discussion
5.2.1 Defects
First, the milled surfaces were inspected for surface defects. Noticeably, all surfaces milled with a width of cut smaller than the maximum height of the surface \(\overline{S_{z}}\) have surface defects. This was predicted by the model for the machining allowance (Eq. 1).
In Table 5 it is shown whether surface defects were found on the surfaces milled with 100 % and 125 % of \(\overline{S_{z}}\) as width of cut.
Nine out of twelve surfaces at 100 % \(\overline{S_{z}}\) as width of cut display surface defects. Of the surfaces milled at 125 % \(\overline{S_{z}}\) only one presents a surface defect.
5.2.2 Waviness and surface roughness
The surface properties of each surface with different widths of cut were measured individually, as shown in Fig. 7.
According to DIN EN ISO 4288 [23], measurements should be taken in the direction where the highest values for the surface roughness and waviness are to be expected. For a peripherally milled surface this corresponds to the feed direction. Therefore, the measurements were only taken in Y-direction and the waviness Wz was measured with the same filters applied as beforehand. A total of eleven profiles was measured for each surface with a distance of 40 px from each other.
In Fig. 8 the resulting surface characteristics after peripheral milling are displayed. For a width of cut of 0–75 % of the \(\overline{S_{z}}\) -value the maximum surface roughness Rz and maximum waviness Wz were evaluated as before. For a total width of cut of 100 % and 125 % \(\overline{S_{z}}\) the surface roughness was within the range of the measurement accuracy. Therefore, the maximum primary height Pz was measured. No filters (Sect. 4.1) were applied. Though the variation in the resulting surface waviness Wz is large, a trend of decreasing waviness with increasing width of cut can be observed.
Usually with milling a surface roughness Ra of 0.8–6.3 µm can be achieved [27]. For a total width of cut of 125 % of the \(\overline{S_{z}}\) -value the maximum primary height Pz is within this range. Therefore, Ra is expected also to be within the necessary range.
5.3 Conclusion
By removing an amount of material corresponding to the measured surface characteristics of the near-net shaped WAAM component, final part quality for the surface roughness can be achieved, as shown in Fig. 8.
This result is independent of the welding parameters and the surface roughness of the near-net shaped WAAM part. Conclusively, the model for the calculation of the machining allowance (Eq. 1) is applicable. However, based on these results, removing 100 % of the maximum height of the surface is not enough to achieve final part quality. To ensure process stability, 125 % should be removed. As these experiments represent only a small range of welding parameters, further research should be carried out.
Validating Eq. 1 is the first step into fully automating the process chain consisting of WAAM and milling. In order to save the time of lengthy milling tests on every new part that is to be produced, the necessary machining allowance needs to be known before the WAAM process. If that MA can be calculated based on the machining setup and the surface characteristics, then the manufacture of only one test part, to measure the surface characteristics, is necessary. This possiblity was shown by partially validating Eq. 1. One step further, if a model can be found to predict the surface characteristics based on the welding torch movement no such test part is necessary and first time right, as well as full automation, could be achieved. That such a model could be found was shown in Sect. 4, where it was demonstrated, that the surface characteristics correlate to the wavelength of the torch movement.
6 Summary and outlook
In this study the surface characteristics of wire and arc manufactured parts were analyzed. At first, the surface waviness was found to correlate to the welding torch movement. Then, a model was proposed to calculate the necessary machining allowance for post-machining of WAAM parts, based on measuring the deviations of the actual WAAM component from an ideal one.
Finally, the model was partially validated by peripheral milling of WAAM parts. Removing 125 % of the maximum height of the surface was shown to result in a high surface quality. As a next step, the deviations in microstructure and position should be analyzed, and more studies should be carried out on the form, the waviness and the surface roughness. This should be combined with a prediction of the WAAM part based on the welding torch tool path. As a result, the necessary percentage of material removal becomes known and first time right quality is achievable. Finally, the method needs to be validated on an industrial level and its applicability in an industrial setting tested.
References
EUROPEAN COMMISSION, Flightpath 2050: Europe’s vision for aviation ; maintaining global leadership and serving society’s needs ; report of the High-Level Group on Aviation Research. Policy / European Commission, Luxembourg: Publ. Off. of the Europ. Union, 2011
Williams JC, Starke EA (2003) Progress in structural materials for aerospace systems11. The golden Jubilee issue-selected topics in materials Science and Engineering: Past, Present and Future, edited by S. Suresh. Acta Materialia 51(19):5775–5799
Martina F and Williams S (2015) Wire + arc additive manufacturing vs. traditional machining from solid: a cost comparison. Report, Cranfield University
Denkena B, Jacob S (2015) Approach for increasing the resource efficiency for the production process of titanium structural components. Procedia CIRP 35:45–49
Davim JP (ed) (2014) Machining of titanium alloys. Springer Materials Forming, Machining and Tribology, Heidelberg
Fuchs C, Baier D, Elitzer D, Kleinwort R, Bachmann A, Zaeh MF (2019) Additive manufacturing for structural components in aerospace engineering. ZWF Zeitschrift für wirtschaftlichen Fabrikbetrieb 114(7):431–434
Kutz M. ed. (2015) Mechanical engineers’ handbook: manufacturing and management. Hoboken: Wiley, fourth edition ed
International Organization for Standardization, “Titanium and titanium wrought alloys forgings (hammer and drop forgings)—Technical specification,” March 2012
Urbanic RJ, Hedrick RW, Burford CG (2017) A process planning framework and virtual representation for bead-based additive manufacturing processes. Int J Adv Manuf Technol 90(1–4):361–376
Manogharan G (2014) Hybrid Manufacturing: Analysis of Integrating Additive and Subtractive Methods. Dissertation, North Carolina State University, Raleigh, North Carolina
Karunakaran KP, Suryakumar S, Pushpa V, Akula S (2010) Low cost integration of additive and subtractive processes for hybrid layered manufacturing. Robot Comput Integrated Manuf 26(5):490–499
Frank M, Harrysson O, Wysk R, Niechen C, Srinivasan H, Hou G, and Keough C (2017) Direct additive subtractive hybrid manufacturing (DASH)—an out of envelope method. In: Proceedings of the 28th annual international symposium on solid freeform fabrication
Li F, Chen S, Shi J, Tian H, Zhao Y (2017) Evaluation and optimization of a hybrid manufacturing process combining wire arc additive manufacturing with Milling for the Fabrication of Stiffened Panels. Appl Sci 7(12):1233
Richard HA, Schramm B, Zipsner T (2019) Additive Fertigung von Bauteilen und Strukturen. Springer Fachmedien Wiesbaden, Wiesbaden
Milewski JO (2017) Additive manufacturing of metals: from fundamental technology to Rocket Nozzles, medical implants, and custom jewelry, vol 258 of Springer series in materials science. Cham: Springer International Publishing
Stucker B, Qu X (2003) A finish machining strategy for rapid manufactured parts and tools. Rapid Prototyping J 9(4):194–200
Dietz SR (2017) Prozessentwicklung und ökonomische Bewertung der automatisierten Nachbearbeitung von additiv gefertigten Dentalunikaten. Dissertation, Shaker Verlag GmbH
Williams SW, Martina F, Addison AC, Ding J, Pardal G, Colegrove P (2016) Wire + Arc additive manufacturing. Materials Sci Technol 32(7):641–647
Suryakumar S, Karunakaran KP, Bernard A, Chandrasekhar U, Raghavender N, Sharma D (2011) Weld bead modeling and process optimization in hybrid layered manufacturing. Comput Aided Des 43(4):331–344
Deutsches Institut fuer Normung, “Form deviations—Concepts—Classification system,” June 1982
Whitehouse DJ (1994) Handbook of surface metrology. Inst. of Physics Publ, Bristol
Baufeld B, van der Biest O, Gault R, Ridgway K (2011) Manufacturing Ti-6Al-4V components by shaped metal deposition: microstructure and mechanical properties. IOP Conference Series: Materials Science and Engineering 26:012001
International Organization for Standardization, “Geometrical Product Specifications (GPS) - Surface texture; Profile method—Rules and procedures for the assessment of surface texture,” April 1998
International organization for standardization, “Geometrical product specifications (GPS)—Surface texture: areal: Part 2: terms, definitions and surface texture parameters,” February 2019
Deutsches Institut fuer Normung, “Geometrical Product Specifications (GPS)—Surface texture: profile method: terms, definitions and surface texture parameters,” July 2010
International organization for standardization, “Geometrical product specifications—geometrical tolerancing: tolerances of form, orientation, location and run-out,” September 2017
Whitehouse D (2002) “Surface metrology and manufacture,” in Surfaces and Their Measurement, pp 96–140, Elsevier
Acknowledgements
A part of this research was carried out within the research project REGULUS, funded by the Federal Ministry for Economic Affairs and Energy (BMWi) (grant number 20W1709D) and supervised by the German Aerospace Center e. V. (DLR). The authors would like to thank the BMWi as well as the DLR for their support. Furthermore, the authors would like to thank Mr. Michael Launer for the preparation and realization of the experimental study.
Funding
Open Access funding provided by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fuchs, C., Baier, D., Semm, T. et al. Determining the machining allowance for WAAM parts. Prod. Eng. Res. Devel. 14, 629–637 (2020). https://doi.org/10.1007/s11740-020-00982-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11740-020-00982-9