Skip to main content
SpringerLink
Log in

Multi-population particle swarm optimization algorithm for automatic design of steel frames

  • Research Article
  • Published:
Frontiers of Structural and Civil Engineering Aims and scope Submit manuscript

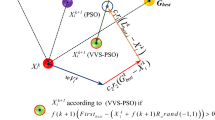
Abstract

Steel structures are widely used; however, their traditional design method is a trial-and-error procedure which is neither efficient nor cost effective. Therefore, a multi-population particle swarm optimization (MPPSO) algorithm is developed to optimize the weight of steel frames according to standard design codes. Modifications are made to improve the algorithm performances including the constraint-based strategy, piecewise mean learning strategy and multi-population cooperative strategy. The proposed method is tested against the representative frame taken from American standards and against other steel frames matching Chinese design codes. The related parameter influences on optimization results are discussed. For the representative frame, MPPSO can achieve greater efficiency through reduction of the number of analyses by more than 65% and can obtain frame with the weight for at least 2.4% lighter. A similar trend can also be observed in cases subjected to Chinese design codes. In addition, a migration interval of 1 and the number of populations as 5 are recommended to obtain better MPPSO results. The purpose of the study is to propose a method with high efficiency and robustness that is not confined to structural scales and design codes. It aims to provide a reference for automatic structural optimization design problems even with dimensional complexity. The proposed method can be easily generalized to the optimization problem of other structural systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Zhang Y, He Z. Seismic collapse risk assessment of super high-rise buildings considering modeling uncertainty: A case study. Structural Design of Tall and Special Buildings, 2020, 29(3): e1687

    Article  Google Scholar 

  2. Lai X, He Z, Wu Y. Elastic inter-story drift seismic demand estimate of super high-rise buildings using coupled flexural-shear model with mass and stiffness non-uniformities. Engineering Structures, 2021, 226: 111378

    Article  Google Scholar 

  3. Hervé Poh’sié G, Chisari C, Rinaldin G, Fragiacomo M, Amadio C, Ceccotti A. Application of a translational tuned mass damper designed by means of genetic algorithms on a multistory cross-laminated timber building. Journal of Structural Engineering, 2016, 142(4): E4015008

    Article  Google Scholar 

  4. Ma L, Bai Y, Zhang J. Vertical deformation analysis of a high-rise building with high-position connections. Structural Design of Tall and Special Buildings, 2020, 29(15): e1787

    Article  Google Scholar 

  5. Liu J P, Zhao M, Zhou J W. Seismic response of column supported tanks considering uplift effect and soil-structure interaction. Earthquake Engineering & Structural Dynamics, 2023, 52(5): 1578–1592

    Article  Google Scholar 

  6. Pechorskaya S A, Galishnikova V V, Gebreslassie S B, Damir H Y. Structural analysis of high-rise building using ETABS and RSA software. Structural Mechanics of Engineering Constructions and Buildings, 2021, 17(2): 133–139

    Article  Google Scholar 

  7. Zhao J, Zhen Z. PKPM and SAP2000 software on a layer of engineering aseismic structure performance analysis based on structure mechanics. Advanced Materials Research, 2013, 788: 498–501

    Article  Google Scholar 

  8. Wang F, Shi Q, Wang P. Seismic behaviour of reinforced concrete frame structures with all steel assembled Q195 low yield buckling restrained braces. Structures, 2021, 30: 756–773

    Article  Google Scholar 

  9. Shan W, Ding Y, Zhou J. Automatic structural optimization design using sensitivity-based method. Structures, 2022, 46: 99–108

    Article  Google Scholar 

  10. Babaei S, Zarfam P. Optimization of shape memory alloy braces for concentrically braced steel braced frames. Open Engineering, 2019, 9(1): 697–708

    Article  Google Scholar 

  11. Shen Y, Branscomb D. Orientation optimization in anisotropic materials using gradient descent method. Composite Structures, 2020, 234: 111680

    Article  Google Scholar 

  12. Li Y, Duan R, Li Q S, Li Y G, Huang X. Wind-resistant optimal design of tall buildings based on improved genetic algorithm. Structures, 2020, 27: 2182–2191

    Article  Google Scholar 

  13. Es-Haghi M S, Shishegaran A, Rabczuk T. Evaluation of a novel asymmetric genetic algorithm to optimize the structural design of 3D regular and irregular steel frames. Frontiers of Structural and Civil Engineering, 2020, 14(5): 1110–1130

    Article  Google Scholar 

  14. Jarrahi H, Asadi A, Khatibinia M, Etedali S, Samadi A. Simultaneous optimization of placement and parameters of rotational friction dampers for seismic-excited steel moment-resisting frames. Soil Dynamics and Earthquake Engineering, 2020, 136: 106193

    Article  Google Scholar 

  15. Degertekin S O, Hayalioglu M S, Gorgun H. Optimum design of geometrically non-linear steel frames with semi-rigid connections using a harmony search algorithm. Steel and Composite Structures, 2009, 9(6): 535–555

    Article  Google Scholar 

  16. Gholizadeh S, Shahrezaei A M. Optimal placement of steel plate shear walls for steel frames by bat algorithm. Structural Design of Tall and Special Buildings, 2015, 24(1): 1–18

    Article  Google Scholar 

  17. Gholizadeh S, Poorhoseini H. Seismic layout optimization of steel braced frames by an improved dolphin echolocation algorithm. Structural and Multidisciplinary Optimization, 2016, 54(4): 1011–1029

    Article  Google Scholar 

  18. Çarbaş S. Optimum structural design of spatial steel frames via biogeography-based optimization. Neural Computing & Applications, 2017, 28(6): 1525–1539

    Article  Google Scholar 

  19. Kaveh A, Khodadadi N, Azar B F, Talatahari S. Optimal design of large-scale frames with an advanced charged system search algorithm using box-shaped sections. Engineering with Computers, 2021, 37(4): 2521–2541

    Article  Google Scholar 

  20. Talatahari S, Gandomi A H, Yang X S, Deb S. Optimum design of frame structures using the eagle strategy with differential evolution. Engineering Structures, 2015, 91: 16–25

    Article  Google Scholar 

  21. Dadkhah M, Kamgar R, Heidarzadeh H, Jakubczyk-Galczyńska A, Jankowski R. Improvement of performance level of steel moment-resisting frames using tuned mass damper system. Applied Sciences, 2020, 10(10): 3403

    Article  Google Scholar 

  22. Shishegaran A, Khalili M R, Karami B, Rabczuk T, Shishegaran A. Computational predictions for estimating the maximum deflection of reinforced concrete panels subjected to the blast load. International Journal of Impact Engineering, 2020, 139: 103527

    Article  Google Scholar 

  23. Shishegaran A, Varaee H, Rabczuk T, Shishegaran G. High correlated variables creator machine: prediction of the compressive strength of concrete. Computers & Structures, 2021, 247: 106479

    Article  Google Scholar 

  24. Shishegaran A, Saeedi M, Mirvalad S, Korayem A H. Computational predictions for estimating the performance of flexural and compressive strength of epoxy resin-based artificial stones. Engineering with Computers, 2023, 39(1): 347–372

    Article  Google Scholar 

  25. Shishegaran A, Karami B, Safari Danalou E, Varaee H, Rabczuk T. Computational predictions for predicting the performance of steel panel shear wall under explosive loads. Engineering Computations, 2021, 38(9): 3564–3589

    Article  Google Scholar 

  26. Karami B, Shishegaran A, Taghavizade H, Rabczuk T. Presenting innovative ensemble model for prediction of the load carrying capacity of composite castellated steel beam under fire. Structures, 2021, 33: 4031–4052

    Article  Google Scholar 

  27. Liu R, Li J, Fan J, Mu C, Jiao L. A coevolutionary technique based on multi-swarm particle swarm optimization for dynamic multi-objective optimization. European Journal of Operational Research, 2017, 261(3): 1028–1051

    Article  MathSciNet  Google Scholar 

  28. Yazdani D, Nasiri B, Sepas-Moghaddam A, Meybodi M R. A novel multi-swarm algorithm for optimization in dynamic environments based on particle swarm optimization. Applied Soft Computing, 2013, 13(4): 2144–2158

    Article  Google Scholar 

  29. Li W, Meng X, Huang Y, Fu Z H. Multipopulation cooperative particle swarm optimization with a mixed mutation strategy. Information Sciences, 2020, 529: 179–196

    Article  MathSciNet  Google Scholar 

  30. Han Y, Gu X. Improved multipopulation discrete differential evolution algorithm for the scheduling of multipurpose batch plants. Industrial & Engineering Chemistry Research, 2021, 60(15): 5530–5547

    Article  Google Scholar 

  31. Nie W, Liu S, Yin H, Lu S, Zhao D, Xu H. Application of the improved multipopulation genetic algorithm in the TMD controlled system considering soil-structure interaction. Advances in Civil Engineering, 2022, 2022: 8212766

    Article  Google Scholar 

  32. Farshchin M, Maniat M, Camp C V, Pezeshk S. School based optimization algorithm for design of steel frames. Engineering Structures, 2018, 171: 326–335

    Article  Google Scholar 

  33. Farshchin M, Camp C V, Maniat M. Optimal design of truss structures for size and shape with frequency constraints using a collaborative optimization strategy. Expert Systems with Applications, 2016, 66: 203–218

    Article  Google Scholar 

  34. GB 50011-2010. Code for Seismic Design of Buildings. Beijing: Standards Press of China, 2010 (in Chinese)

    Google Scholar 

  35. JGJ 99-2015. Technical specification for steel structure of tall building. Beijing: China Architecture and Building Press, 2015 (in Chinese)

    Google Scholar 

  36. GB 50017-2017. Standard for design of steel structures. Beijing: China Architecture and Building Press, 2017 (in Chinese)

    Google Scholar 

  37. American Institute of Steel Construction. Manual of Steel Construction: Load & Resistance Factor Design. 3rd ed. Chicago: American Institute of Steel Construction, 2001

    Google Scholar 

  38. Camp C V, Bichon B J, Stovall S P. Design of steel frames using ant colony optimization. Journal of Structural Engineering, 2005, 131(3): 369–379

    Article  Google Scholar 

  39. Kaveh A, Talatahari S. An improved ant colony optimization for the design of planar steel frames. Engineering Structures, 2010, 32(3): 864–873

    Article  Google Scholar 

  40. Degertekin S O. Optimum design of steel frames using harmony search algorithm. Structural and Multidisciplinary Optimization, 2008, 36(4): 393–401

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by National Natural Science Foundation of China (Grant Nos. 52308142 and 52208185), Postdoctoral Fellowship Program of CPSF (No. GZC20233334), Special Support of Chongqing Postdoctoral Science Foundation (No. 2021XM2039) and National Key Research and Development Program of China (No. 2022YFC3801700).

Author information

Authors and Affiliations

  1. Institute of Smart City and Intelligent Transportation, Southwest Jiaotong University, Chengdu, 610000, China

    Wenchen Shan

  2. School of Civil Engineering, Chongqing University, Chongqing, 400045, China

    Jiepeng Liu, Yao Ding & Junwen Zhou

  3. Department of Civil Engineering, the Pennsylvania State University, Middletown, PA, 17057, USA

    Y. Frank Chen

Authors
  1. Wenchen Shan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiepeng Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yao Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Y. Frank Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Junwen Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Junwen Zhou.

Ethics declarations

Competing interests The authors declare that they have no competing interests.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shan, W., Liu, J., Ding, Y. et al. Multi-population particle swarm optimization algorithm for automatic design of steel frames. Front. Struct. Civ. Eng. 18, 89–103 (2024). https://doi.org/10.1007/s11709-024-1037-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11709-024-1037-7

Keywords

Search

Navigation