Abstract
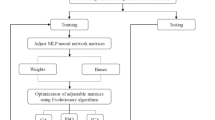
Currently, the vertical drain consolidation problem is solved by numerous analytical solutions, such as time-dependent solutions and linear or parabolic radial drainage in the smear zone, and no artificial intelligence (AI) approach has been applied. Thus, in this study, a new hybrid model based on deep neural networks (DNNs), particle swarm optimization (PSO), and genetic algorithms (GAs) is proposed to solve this problem. The DNN can effectively simulate any sophisticated equation, and the PSO and GA can optimize the selected DNN and improve the performance of the prediction model. In the present study, analytical solutions to vertical drains in the literature are incorporated into the DNN—PSO and DNN—GA prediction models with three different radial drainage patterns in the smear zone under time-dependent loading. The verification performed with analytical solutions and measurements from three full-scale embankment tests revealed promising applications of the proposed approach.
Similar content being viewed by others
Abbreviations
- c h :
-
coefficient of consolidation in the horizontal direction
- c v :
-
coefficient of consolidation in the vertical direction
- F c :
-
parameter to reflect the effect of the decay pattern
- H :
-
soil thickness
- k d :
-
coefficient of permeability of the drain
- k h :
-
horizontal coefficient of permeability
- k s :
-
horizontal coefficient of permeability of the smeared zone
- k v :
-
vertical coefficient of permeability
- m v :
-
coefficient of volume compressibility
- q w :
-
discharge capacity
- r d :
-
drain radius
- r e :
-
equivalent radius of the influence zone
- r s :
-
smeared zone radius
- u :
-
excess pore water pressure
- \(\bar{u}\) :
-
average excess pore water pressure
- τ(t):
-
the surcharge load
- ε v :
-
vertical strain
- γ w :
-
unit weight of water
References
Guo H, Zhuang X, Rabczuk T. A deep collocation method for the bending analysis of Kirchhoff plate. Computers, Materials & Continua, 2019, 59(2): 433–156
Anitescu C, Atroshchenko E, Alajlan N, Rabczuk T. Artificial neural network methods for the solution of second order boundary value problems. Computers, Materials & Continua, 2019, 59(1): 345–359
Samaniego E, Anitescu C, Goswami S, Nguyen-Thanh V M, Guo H, Hamdia K, Zhuang X, Rabczuk T. An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications. Computer Methods in Applied Mechanics and Engineering, 2020, 362: 112790
Guo H, Zhuang X, Meng X, Rabczuk T. Integrated intelligent Jaya Runge-Kutta method for solving Falkner-Skan equations for various wedge angles. 2020, arXiv:2010.05682
Hamdia K M, Zhuang X, Rabczuk T. An efficient optimization approach for designing machine learning models based on genetic algorithm. Neural Computing & Applications, 2021, 33(6): 1923–1933
Zhuang X, Guo H, Alajlan N, Rabczuk T. Deep autoencoder based energy method for the bending, vibration, and buckling analysis of Kirchhoff plates. European Journal of Mechanics. A, Solids, 2020, 2010: 05698
Ahmad I, Hesham El Naggar M, Khan A N. Artificial neural network application to estimate kinematic soil pile interaction response parameters. Soil Dynamics and Earthquake Engineering, 2007, 27(9): 892–905
Momeni E, Nazir R, Jahed Armaghani D, Maizir H. Prediction of pile bearing capacity using a hybrid genetic algorithm-based ANN. Measurement, 2014, 57: 122–131
Kurup P U, Dudani N K. Neural networks for profiling stress history of clays from PCPT data. Journal of Geotechnical and Geoenvironmental Engineering, 2002, 128(7): 569–579
Lee S J, Lee S R, Kim Y S. An approach to estimate unsaturated shear strength using artificial neural network and hyperbolic formulation. Computers and Geotechnics, 2003, 30(6): 489–503
Ham B T, Nguyen M D, Dao D V, Prakash I, Ly H B, Le T T, Ho L S, Nguyen K T, Ngo T Q, Hoang V, Son L H, Ngo H T T, Tran H T, Do N M, Van Le H, Ho H L, Tien Bui D. Development of artificial intelligence models for the prediction of compression coefficient of soil: An application of Monte Carlo sensitivity analysis. Science of the Total Environment, 2019, 679: 172–184
Beucher A, Møller A B, Greve M H. Artificial neural networks and decision tree classification for predicting soil drainage classes in Denmark. Geoderma, 2019, 352: 351–359
Abbaszadeh Shahri A, Spross J, Johansson F, Larsson S. Landslide susceptibility hazard map in southwest Sweden using artificial neural network. Catena, 2019, 183: 104225
Chen W, Pourghasemi H R, Kornejady A, Zhang N. Landslide spatial modeling: Introducing new ensembles of ANN, MaxEnt, and SVM machine learning techniques. Geoderma, 2017, 305: 314–327
Khanlari G R, Heidari M, Momeni A A, Abdilor Y. Prediction of shear strength parameters of soils using artificial neural networks and multivariate regression methods. Engineering Geology, 2012, 131–132: 11–18
Tiryaki B. Predicting intact rock strength for mechanical excavation using multivariate statistics, artificial neural networks, and regression trees. Engineering Geology, 2008, 99(1–2): 51–60
Bergado D T, Balasubramaniam A S, Fannin R J, Holtz R D. Prefabricated vertical drains (PVDs) in soft Bangkok clay: A case study of the new Bangkok International Airport project. Canadian Geotechnical Journal, 2002, 39(2): 304–315
Bergado D T, Chaiyaput S, Artidteang S, Nguyen T N. Microstructures within and outside the smear zones for soft clay improvement using PVD only, Vacuum-PVD, Thermo-PVD and Thermo-Vacuum-PVD. Geotextiles and Geomembranes, 2020, 48(6): 828–843
Nghia N T, Lam L G, Shukla S K. A new approach to solution for partially penetrated prefabricated vertical drains. International Journal of Geosynthetics and Ground Engineering, 2018, 4(2): 11–17
Nghia-Nguyen T, Shukla S K, Nguyen D D C, Lam L G, H-Dang P, Nguyen P C. A new discrete method for solution to consolidation problem of ground with vertical drains subjected to surcharge and vacuum loadings. Engineering Computations, 2019, 37(4): 1213–1236
Nguyen T N, Bergado D T, Kikumoto M, Dang H P, Chaiyaput S, Nguyen P C. A simple solution for prefabricated vertical drain with surcharge preloading combined with vacuum consolidation. Geotextiles and Geomembranes, 2021, 49(1): 304–322
Shome R, Tang W N, Song C, Mitash C, Kourtev H, Yu J, Boularias A, Bekris K E. Towards robust product packing with a minimalistic end-effector. In: 2019 International Conference on Robotics and Automation (ICRA). IEEE, 2019, 9007–9013
Lu M M, Xie K H, Wang S Y. Consolidation of vertical drain with depth-varying stress induced by multi-stage loading. Computers and Geotechnics, 2011, 38(8): 1096–1011
Tang X W, Onitsuka K. Consolidation by vertical drains under time-dependent loading. International Journal for Numerical and Analytical Methods in Geomechanics, 2000, 24(9): 739–751
Rujikiatkamjorn C, Indraratna B. Analytical solution for radial consolidation considering soil structure characteristics. Canadian Geotechnical Journal, 2015, 52(7): 947–960
Xie K H, Lu M M, Liu G B. Equal strain consolidation for stone columns reinforced foundation. International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(15): 1721–1735
Dey N, Borra S, Ashour A Sand Shi F. Machine Learning in Bio-Signal Analysis and Diagnostic Imaging. Academic Press, 2018, 159–182
Kennedy J, Eberhart R. Particle swarm optimization. In: Proceedings of the IEEE International Conference on Neural Networks. IEEE, 1995, 4: 1942–1948
Golberg D E. Genetic Algorithms in Search, Optimization, and Machine Learning. Addison Wesley, 1989
Van Der Malsburg C. Frank Rosenblatt: Principles of neurodynamics: Perceptrons and the Theory of Brain Mechanisms. In: Palm G, Aertsen A, eds. Brain Theory. Berlin: Springer, 1986, 245–248
Moghaddasi M R, Noorian-Bidgoli M. ICA-ANN, ANN and multiple regression models for prediction of surface settlement caused by tunneling. Tunnelling and Underground Space Technology, 2018, 79: 197–209
Hagan M T, Menhaj M B. Training feedforward networks with the Marquardt algorithm. IEEE Transactions on Neural Networks, 1994, 5(6): 989–993
Rafiq M Y, Bugmann G, Easterbrook D J. Neural network design for engineering applications. Computers & Structures, 2001, 79(17): 1541–1552
Prechelt L. Early stopping—But when, neural networks: Tricks of the trade. In: Montavon G, Orr G B, Müller K R, eds. Neural Networks: Tricks of the Trade. Springer, 1998, 55–69
Huang S C, Huang Y F. Bounds on the number of hidden neurons in multilayer perceptrons. IEEE Transactions on Neural Networks, 1991, 2(1): 47–55
Kanellopoulos I, Wilkinson G G. Strategies and best practice for neural network image classification. International Journal of Remote Sensing, 1997, 18(4): 711–725
Lin D G, Chang K T. Three-dimensional numerical modelling of soft ground improved by prefabricated vertical drains. Geosynthetics International, 2009, 16(5): 339–353
Lam L G, Bergado D T, Hino T. PVD improvement of soft Bangkok clay with and without vacuum preloading using analytical and numerical analyses. Geotextiles and Geomembranes, 2015, 43(6): 547–557
Bergado D T, Manivannan R, Balasubramaniam A S. Proposed criteria for discharge capacity of prefabricated vertical drains. Geotextiles and Geomembranes, 1996, 14(9): 481–505
Deng Y B, Liu G B, Lu M M, Xie K H. Consolidation behavior of soft deposits considering the variation of prefabricated vertical drain discharge capacity. Computers and Geotechnics, 2014, 62: 310–316
Acknowledgements
Financial support provided by Ho Chi Minh City Open University is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Nghia-Nguyen, T., Kikumoto, M., Khatir, S. et al. Data-driven approach to solve vertical drain under time-dependent loading. Front. Struct. Civ. Eng. 15, 696–711 (2021). https://doi.org/10.1007/s11709-021-0727-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11709-021-0727-7