Skip to main content
SpringerLink
Log in

Classical state feedback controller for nonlinear systems using mean value theorem: closed loop-FOC of PMSM motor application

  • Research Article
  • Published:
Frontiers in Energy Aims and scope Submit manuscript

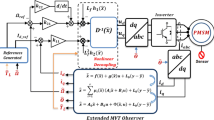
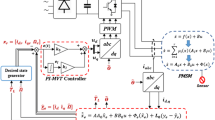
Abstract

The problem of state feedback controllers for a class of Takagi-Sugeno (T-S) Lipschitz nonlinear systems is investigated. A simple systematic and useful synthesis method is proposed based on the use of the differential mean value theorem (DMVT) and convex theory. The proposed design approach is based on the mean value theorem (MVT) to express the nonlinear error dynamics as a convex combination of known matrices with time varying coefficients as linear parameter varying (LPV) systems. Using the Lyapunov theory, stability conditions are obtained and expressed in terms of linear matrix inequalities (LMIs). The controller gains are then obtained by solving linear matrix inequalities. The effectiveness of the proposed approach for closed loop-field oriented control (CL-FOC) of permanent magnet synchronous machine (PMSM) drives is demonstrated through an illustrative simulation for the proof of these approaches. Furthermore, an extension for controller design with parameter uncertainties and perturbation performance is discussed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ichalal D, Arioui H, Mammar S. Observer design for two-wheeled vehicle: a Takagi-Sugeno approach with unmeasurable premise variables. In: Proceedings of the 19th Mediterranean Conference on Control and Automation. Corfu, Greece, 2011, 1–6

    Google Scholar 

  2. Pertew A M, Marquez H J, Zhao Q. H1 observer design for Lipschitz nonlinear systems. IEEE Transactions on Automatic Control, 2006, 51(7): 1211–1216

    Article  MathSciNet  Google Scholar 

  3. Luenberger D G. An introduction to observers. IEEE Transactions on Automatic Control, 1971, 16(6): 596–602

    Article  MathSciNet  Google Scholar 

  4. Rajamani R. Observers for Lipschitz nonlinear systems. IEEE Transactions on Automatic Control, 1998, 43(3): 397–401

    Article  MATH  MathSciNet  Google Scholar 

  5. Bara G I, Daafouz J, Kratz F, Ragot J. Parameter dependent state observer design for affine LPV systems. International Journal of Control, 2001, 74(16): 1601–1611

    Article  MATH  MathSciNet  Google Scholar 

  6. Zemouche A, Boutayeb M, Bara G I. Observer design for nonlinear systems: an approach based on the differential mean value theorem. In: Proceedings of the 44th IEEE Conference on Decision and Control. Seville, Spain, 2005, 6353–6358

    Google Scholar 

  7. Phanomchoeng G, Rajamani R, Piyabongkarn D. Nonlinear observer for bounded Jacobian systems, with applications to automotive slip angle estimation. IEEE Transactions on Automatic Control, 2011, 56(5): 1163–1170

    Article  MathSciNet  Google Scholar 

  8. Tanaka K, Wang H O. Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach. New York: Wiley-Interscience, 2001

    Book  Google Scholar 

  9. Baranyi P. TP model transformation as a way to LMI-based controller design. IEEE Transactions on Industrial Electronics, 2004, 51(2): 387–400

    Article  Google Scholar 

  10. Merzoug M, Naceri F. Comparison of field-oriented control and direct torque control for permanent magnet synchronous motor (PMSM). International Journal of Electrical, Computer, Energetic, Electronics and Communication Engineering, 2008, 2(9): 107–112

    Google Scholar 

  11. Molavi R, Khaburi D A. Optimal control strategies for speed control of permanent-magnet synchronous motor drives. Proceedings of World Academy of Science Engineering and Technology, 2008, 44: 428

    Google Scholar 

  12. Štulrajter M, Hrabovcov¨¢ V, Franko M. Permanent magnets synchronous motor control theory. Journal of Electrical Engineering, 2007, 58(2): 79–84

    Google Scholar 

  13. Novotny D, Lipo T. Vector Control and Dynamics of AC Drives. New York: Oxford University Press, 1996

    Google Scholar 

  14. Solsona J, Valla M I, Muravchik C. Nonlinear control of a permanent magnet synchronous motor with disturbance torque estimation. IEEE Transactions on Energy Conversion, 2000, 15(2): 163–168

    Article  Google Scholar 

  15. Shi J L, Liu T H, Chang Y C. Optimal controller design of a sensorless PMSM control system. Industrial Electronics Society, 2005. IECON 2005. 31st Annual Conference of IEEE, 2005.

    Google Scholar 

  16. Zemouche A, Boutayeb M, Bara G I. Observers for a class of Lipschitz systems with extension to H1 performance analysis. Systems & Control Letters, 2008, 57(1): 18–27

    Article  MATH  MathSciNet  Google Scholar 

  17. Sahoo P K, Riedel T. Mean Value Theorems and Functional Equations. New Jersey:World Scientific Publishing Company, 1999

    Google Scholar 

  18. Bergsten P, Palm R, Driankov D. Observers for Takagi-Sugeno fuzzy systems. IEEE Transactions on Systems, Man, and Cybernetics. Part B, Cybernetics, 2002, 32(1): 114–121

    Article  Google Scholar 

  19. Raghavan S, Hedrick J K. Observer design for a class of nonlinear systems. International Journal of Control, 1994, 59(2): 515–528

    Article  MATH  MathSciNet  Google Scholar 

  20. Rahman M A, Vilathgamuwa D M, Uddin M N, Tseng K J. Nonlinear control of interior permanent-magnet synchronous motor. IEEE Transactions on Industry Applications, 2003, 39(2): 408–416

    Article  Google Scholar 

  21. Ren H, Liu D. Nonlinear feedback control of chaos in permanent magnet synchronous motor. IEEE Transactions on Circuits and Systems II: Express Briefs, 2006, 53(1): 45–50

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. LGEB Laboratory, Department of Electrical Engineering, University of Biskra, Biskra, BP 145, Algeria

    Abrar Allag, Abdelhamid Benakcha & Meriem Allag

  2. R&D, Industrial Hybrid Vehicle Applications, Belfort, 90010, France

    Ismail Zein & Mohamed Yacine Ayad

Authors
  1. Abrar Allag
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Abdelhamid Benakcha
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Meriem Allag
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ismail Zein
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mohamed Yacine Ayad
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Abrar Allag.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Allag, A., Benakcha, A., Allag, M. et al. Classical state feedback controller for nonlinear systems using mean value theorem: closed loop-FOC of PMSM motor application. Front. Energy 9, 413–425 (2015). https://doi.org/10.1007/s11708-015-0379-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11708-015-0379-1

Keywords

Search

Navigation