Skip to main content
SpringerLink
Log in

Effect of Fatigue Damage Parameter on the Cumulative Life of a Turbine Rotor Under Multiaxial Loading

  • Technical Article---Peer-Reviewed
  • Published:
Journal of Failure Analysis and Prevention Aims and scope Submit manuscript

Abstract

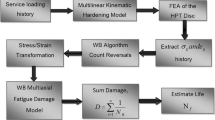
The effect of the fatigue damage parameter on the cumulative life of a high-speed turbine rotor has been estimated through finite element approach. Two most commonly used multiaxial fatigue damage models based on critical plane approach-Fatemi Socie (FS) model, and Kandil Brown and Miller model (KBM) have been used to estimate the fatigue life. Structural integrity test was carried out in spin test facility to validate the simulation results. KBM model for fatigue life estimation and LMP model for creep damage predicted a cumulative life within a factor of 1.5 scatter band of the experimental value. The combination of FS model for fatigue life estimation and LMP model could predict cumulative life only within a scatter band of 2. Some of the shortcomings attributed to LDS method can be obviated using a suitable fatigue damage parameter. The study provides invaluable input and confidence for the life prediction of high-speed gas turbine rotors.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Abbreviations

b :

Fatigue strength exponent

c :

Fatigue ductility exponent

σ ′f :

Fatigue strength coefficient

ɛ ′f :

Fatigue ductility coefficient

b o :

Fatigue strength exponent in torsion

τ ′f :

Shear fatigue strength coefficient

γ ′f :

Shear fatigue ductility coefficient

c o :

Fatigue ductility exponent in torsion

E :

Young's modulus

G :

Shear modulus

∆ɛ eq :

Equivalent von Mises strain range

∆γ eq :

Equivalent shear strain range

∆ɛ 1 :

Maximum principal strain range

σ n,max :

Maximum normal stress

∆ɛ n :

Maximum normal strain range

σ m :

Mean stress

σ a :

Alternating stress

∆γ max :

Maximum shear strain range

k :

Material constant

S :

Material constant

References

  1. H. Cohen, G.F.C. Rogers, H.I.H. Saravanamuttoo, Gas Turbine Theory, vol. 5 (Wiley, New York, 2001)

    Google Scholar 

  2. B.A. Cowles, High cycle fatigue in aircraft gas turbines—an industry perspective. Int. J. Fract. 80(2–3), 147–163 (1996)

    Article  Google Scholar 

  3. S.P. Zhu, H.Z. Huang, Y. Liu et al., An efficient life prediction methodology for low cycle fatigue-creep based on ductility exhaustion theory. Int. J. Damage Mech. 22(4), 556–571 (2012)

    Article  Google Scholar 

  4. S.P. Zhu, H.Z. Huang, P.L. He et al., A generalized energy-based fatigue–creep damage parameter for life prediction of turbine disk alloys. Eng. Fract. Mech. 90, 89–100 (2012)

    Article  Google Scholar 

  5. S.S. Manson, G. Halford, A method of estimating high temperature low cycle fatigue behaviour of materials, in Proceedings of Int. Conference on Thermal and High Strain Fatigue (Metals and Metallurgy Trust, London, 1967), pp. 154–170.

  6. S. Majumdar, P.S. Maiya, A damage equation for creep–fatigue interaction, in Winter annual meeting of ASME, New York, 1976, pp. 323–336.

  7. T. Goswami, Low cycle fatigue life prediction—a new model. Int. J. Fatigue 19(2), 109–115 (1997)

    Article  Google Scholar 

  8. S.S. Manson, G.R. Halford, M.H. Hirschberg, Creep–fatigue analysis by strain-range partitioning, in First symposia on design for elevated temperature environment, ASME, 1971, pp. 12–28.

  9. W.J. Ostergren, A damage foundation hold time and frequency effects in elevated temperature low cycle fatigue. J. Test Eval. 4, 327–339 (1967)

    Google Scholar 

  10. A. Fatemi, N. Shamsaei, Multiaxial fatigue damage modelling and some approximations, in Proceedings of International Conference on Multiaxial Fatigue and Fracture (ICMFF9), Italy, 2010.

  11. A. Fatemi, D.E. Socie, A critical plane approach to multiaxial fatigue damage including out of phase loading. Fatigue Fract. Eng. Mater. 11(3), 149–166 (1987)

    Article  Google Scholar 

  12. D.G. Shang, G.Q. Sun, J.H. Chen, N. Cai, Creep-fatigue life prediction under fully reversed multiaxial loading at high temperatures. Int. J. Fatigue 29, 705–712 (2007)

    Article  Google Scholar 

  13. D.G. Shang, D.J. Wang, A new multiaxial fatigue damage model based on the critical plane approach. Int. J. Fatigue 20(3), 241–245 (1998)

    Article  Google Scholar 

  14. U. Kocabicak, M. Firat, A simple approach for multiaxial fatigue damage prediction based on FEM post processing. Mater. Des. 25, 73–82 (2004)

    Article  Google Scholar 

  15. J.F. Besseling, A theory of elastic, initially isotropic material. J. Appl. Mech. 25, 529–536 (1958)

    Google Scholar 

  16. L. Gan, H.-Z. Huang, S.-P. Zhu, Y.-F. Li, Y. Yang, Fatigue reliability analysis of turbine disk alloy using saddle point approximation. Int. J. Turbo Jet Engines 30(3), 217–229 (2013). doi:10.1515/tjj-2013-0020

    Article  Google Scholar 

  17. J.R. Kattus, Purdue Research Foundation 1999; MARM 247. Aerospace Structural Metal Hand Book, code 4218, 1–8

  18. F.R. Larson, J.A. Miller, Time-temperature relationship for rupture and creep stresses. Trans. ASME 74(5), 765–775 (1952)

    Google Scholar 

  19. H.-Z. Huang, J. Gong, M.J. Zuo, S.-P. Zhu, Q. Liao, Fatigue life estimation of an aircraft engine under different load spectrums. Int. J. Turbo Jet Engines 29(4), 259–267 (2012). doi:10.1515/tjj-2012-0017

    Article  Google Scholar 

  20. R.K. Mishra, T. Johney, K. Srinivasan, N. Vaisakhi, B. Raghavendra, Failure analysis of HP turbine blades in a low bypass turbofan engine. J. Fail. Anal. Prev. 13(3), 274–281 (2013). doi:10.1007/s11668-013-9674-5

    Article  Google Scholar 

  21. N.E. Dowling, Mechanical Behaviour of Materials, 2nd edn. (Upper Saddle River, Prentice Hall International, 1999)

    Google Scholar 

  22. J.A. Bannantine, J.J. Comer, J.L. Handrock, Fundamental of Metal Fatigue Analysis (Prentice Hall Inc., New Jersey, 1990), pp. 40–87

    Google Scholar 

  23. S. Suresh, Fatigue of Materials (Cambridge University Press, UK, 2003)

    Google Scholar 

  24. F.A. Kandil, M.W. Brown, K.J. Miller, Biaxial low cycle fatigue failure of 316 stainless steel at elevated temperatures. Metal Struct. 14(22), 203–210 (1982)

    Google Scholar 

  25. F. Garofalo, Fundamentals of Creep and Creep-Rupture in Metals, McMillan Series in Materials Science (McMillan, New York, 1965)

    Google Scholar 

  26. N. Ejaz, I.N. Qureshi, S.A. Rizvi, Creep failure of low pressure turbine blade of an aircraft engine. J. Eng. Failure Anal. 18(6), 1407–1414 (2011)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Aero Engine Research and Design Centre, Hindustan Aeronautics Limited, Bangalore, Karnataka, India

    S. Dileep, S. Esakki Muthu & P. Udayanan

  2. Regional Centre for Military Airworthiness, Bangalore, Karnataka, 560093, India

    R. K. Mishra

Authors
  1. S. Dileep
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Esakki Muthu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. P. Udayanan
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. R. K. Mishra
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. K. Mishra.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dileep, S., Esakki Muthu, S., Udayanan, P. et al. Effect of Fatigue Damage Parameter on the Cumulative Life of a Turbine Rotor Under Multiaxial Loading. J Fail. Anal. and Preven. 16, 612–621 (2016). https://doi.org/10.1007/s11668-016-0127-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11668-016-0127-9

Keywords

Search

Navigation