Introduction

Reliable performance of NiTi medical implants in minimally invasive therapy requires precise knowledge of phase transformation temperatures for triggering pseudoelastic deformation or the shape memory effect (Ref 1, 2). Both effects are based on the well-documented martensitic transformation of NiTi between B19' martensite and B2 austenite (Ref 3). Depending on the material condition, an intermediate R-phase can occur (Ref 4). The phase transformation may be triggered by external stress or a temperature change. Particularly for medical applications, the functional transformation temperatures are of interest that results in an active shape change of the components. Various methods for determining transformation temperatures of NiTi including differential scanning calorimetry (DSC), bend and free recovery tests (BFR), and less conventional methods such as magnetization measurements are documented (Ref 5,6,7). Considering that residual mechanical stress in the material affects the transformation temperatures, the BFR test most closely resembles the application conditions in order to characterize the active response of a NiTi wire or component. Deformation temperatures determined by other methods may yield slightly different values due to the deformation gradients during bending (Ref 8). The standard procedure for BFR tests is specified in the ASTM method F2082-16 (Ref 6). The procedure relies on the continuous measurement of the position of a given location on a previously bent NiTi segment that is in direct contact with a linear variable differential transducer (LVDT). Thus, an additional load is added that again potentially affects the measurement results. While the influence may certainly be negligible for materials extensions of several 100 µm, it must be considered for wires with diameters below 50 µm. Such dimensions are used in novel cardiovascular implants, e.g., because of a lower risk of restenosis (Ref 9, 10). Non-contact approaches for BFR tests facilitate the measurement of transformation temperatures of such thin NiTi wires by eliminating the influence of additional loads.

In previous studies, several non-contact bend and free recovery test methods were presented (Ref 11,12,13,14,15). Non-contact testing is usually applied by tracking the reverse deformation of a single or several spots on a sample. Tracking the lowest point of a bent wire is the non-contact equivalent of measuring the wire in direct contact via an LVDT at a single spot. However, non-contact approaches utilizing optical systems are technically capable of evaluating transformation temperatures on the basis of the entire shape of a part of a wire, e.g., by assessing the change of curvature of a bent wire segment. Such evaluation requires a more complex procedure or the reduction of data sets to only a few data points (Ref 15). The method has the potential to increase flexibility with respect to shape and position of a given sample. Also considering unintentional lateral movement of the entire wire or device, transformation temperatures are expected to be measurable precisely by tracking the curvature. Until present, it remains to be clarified in detail to what extent evaluation of curvature versus evaluation of a single spot on a wire yields consistent results regarding reverse deformation curves and corresponding transformation temperatures.

In the present work, a non-contact BFR tester equipped with a digital camera and two thermocouples placed next to the wire holder was used. The BFR tester allows for high spatial and temperature resolution. The acquired images of the wire shape were subject to evaluation by an in-house software code tracking a single spot or calculating local or mean curvatures. The non-contact BFR tester is capable of determining transformation temperatures of thin NiTi wires with diameters as low as 25 µm. The effect of different routines for identifying and fitting the outline of the wire from the digital images is analyzed and discussed, establishing a basis for understanding effects of evaluation methods on the shape of reverse transformation curves and respective transformation temperatures in non-contact bend and free recovery tests of thin NiTi wires.

Materials and Methods

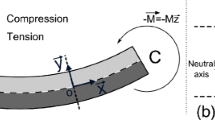
NiTi wires with 50.8 at.% Ni complying with the standard SE508 were used. The as-delivered straight annealed NiTi wires were subjected to a further annealing of 5, 10, and 30 min at 540 °C in air atmosphere for altering the transformation temperatures. Details of the annealing procedure can be found elsewhere (Ref 11). The experimental setup of the BFR tester as used in this study is shown in Fig. 1(a). During each measurement, a straight wire segment of approx. 8 mm length with a mass < 1 mg was placed on an inclined PTFE sample holder in order to minimize friction during testing and to facilitate image acquisition. The camera was positioned perpendicular to the plane of the PTFE sample holder. The PTFE sample holder was fixed to a double-walled brass container inside the inner compartment, submerged in ethanol and placed on a hot plate with a magnetic stirrer. The outer compartment of the container was filled with liquid nitrogen until the ethanol bath reached a temperature < −55 °C. The straight NiTi wire was then bent manually by pushing it down through the wire rests in order to achieve an outer fiber strain of 2.0-2.5%. After bending, the ethanol bath was heated to a temperature of 30 °C at a heating rate of approx. 4 °C/min in accordance with ASTM F2082-16 (Ref 6). During the heating procedure, images were acquired in intervals of 3 s (Fig. 1b). The temperature was monitored simultaneously by two Ni/CrNi thermocouples placed directly above and below the wire (Fig. 1b). All tested wires had fully recovered their initial shape before the final temperature of 30 °C was reached.

Fig. 1
figure 1

(a) Schematic drawing of the non-contact optical bend and free recovery tester. (b) Image of a bent NiTi wire as acquired by the camera system. The thermocouples close to the wire are visible. (c) Binarized image for further optical evaluation

Full size image

Evaluation by image processing was conducted using MATLAB (Ref 16). The acquired images were binarized (Fig. 1c), and the lowest point of the wire was determined for each image, corresponding to an LVDT tracking of the reverse deformation. Due to the increasing temperature, the level of ethanol inside the compartment rose, causing a distortion of the images. The distortion was accounted for by using the fixed positions of the thermocouples as reference points. In a second procedure, the lower outline of the wire was tracked for curvature analysis. The local curvature κ of a graph of a function y(x) is calculated using the following equation (Ref 17):

$$\kappa = \frac{{\frac{{{\text{d}}^2y}}{{{\text{d}}x^2}}}}{{\left( {1 + \left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)^{2} } \right)^{{\frac{3}{2}}} }}$$
(1)

In order to calculate the local wire curvature by Eq 1, an analytical description of the wire shape is required for finding the derivatives \(\frac{{{\text{d}}y}}{{{\text{d}}x}}\) and \(\frac{{{\text{d}}^{2} y}}{{{\text{d}}x^{2} }}\). Accordingly, the wire outline needs to be fitted with a suitable analytical function. In the present work, the wire outline was fitted using second degree and fourth degree polynomials as well as circle segment and ellipse segment functions. Using second degree polynomials, fourth degree polynomials, and ellipse segments, the curvature was averaged over the wire segment for each image. The movement of the lowest wire point / the cumulative change in curvature were scaled in accordance with ASTM F2082-16 so that 0% reverse deformation corresponds to − 55 °C, and 100% reverse deformation corresponds to a completely straight wire. Consistent scaling is a prerequisite to attain reliable BFR results (Ref 18).

Results

The reverse deformation curves attained by tracking the lowest point of the wire and calculating mean curvatures based on fitting the wire outline by second degree and fourth degree polynomials or circle segment functions are shown in Fig. 2. A superimposed martensite-to-austenite and martensite-to-R-phase-to-austenite transformation is observed for the wire annealed for 5 min (Fig. 2a) (Ref 11, 12). A separate martensite-to-R-phase and R-phase-to-austenite transformation is observed for the wire annealed for 10 min (Fig. 2b). A direct martensite-to-austenite transformation is observed for the wire annealed for 30 min (Fig. 2c). The basic shape of the reverse deformation curves is similar for all evaluation methods. Differences between the respective curves are observed in two aspects: (1) a different degree of reverse deformation before the phase transformations occur, and (2) a differing level of noise when the wires become straight at the end of the reverse transformation (see insets in Fig. 2).

Fig. 2
figure 2

Reverse deformation curves obtained by non-contact BFR tests through evaluation of the lowest point of the wire and of the curvature by using second degree polynomial, fourth degree polynomial, and circle segment fits. The insets show the level of noise for the different curvature evaluation methods when the wires become straight. The curves were obtained by testing wires that were subjected to prior annealing for (a) 5 min, (b) 10 min, and (c) 30 min

Full size image

Using ellipse segments for fitting the wire shape resulted in pronounced fluctuations of the calculated curvature and thus of the level of reverse deformation for nearly straight wires (Fig. 3). As a consequence, the horizontal slope at the end of the reverse deformation is obscured. Even reverse deformation levels below zero were calculated for some images, implying a curvature that is larger than the curvature of the wire at − 55 °C. Due to this obvious flaw, ellipse segments as method for fitting the wire shape were disregarded in the further evaluation of transformation temperatures.

Fig. 3
figure 3

Reverse deformation curves of the wire annealed for 5 min obtained through evaluation of the lowest point and of local curvature by using ellipse segment fits

Full size image

For precise evaluation of transformation temperatures, the tangent method as described in ASTM F2082-16 was applied to the reverse deformation curves shown in Fig. 2. The obtained temperatures are listed in Table 1.

Table 1 Transformation temperatures obtained by applying the tangent method to the reverse deformation curves in Fig. 2
Full size table

Discussion

Influence of Evaluation Method on the Shape of Reverse Deformation Curves

In general, the three types of reverse deformation curves shown in Fig. 2 correspond well to those observed in previous research (Ref 11, 12). As mentioned above, a deviation between the curves is observed until the phase transformation occurs, and a different level of noise is visible when the wires become straight at the end of the reverse transformation. The optical evaluation of the lowest wire point and the curvature evaluation of second degree polynomial and circle segment fits produce similar reverse deformation curves with low noise. The curvature evaluation of fourth degree polynomial and ellipse segment fits produces reverse deformation curves with generally a similar shape, but these deformation curves exhibit high noise when analyzing nearly straight wire segments.

A striking difference between the results of the evaluation methods is observed in the reverse deformation curves of the wire annealed for 5 min. The evaluation of the lowest point, corresponding to tracking the reverse deformation in a contact BFR test, shows a simultaneous martensite-to-austenite and martensite-to-R-phase-to-austenite transformation. Accordingly, only R′s and Af are assessable. Further details of the phase transformation, e.g., R′f, remain unclear. However, using second degree polynomial or circle segment fits for evaluation of the curvature change, a two-stage transformation with distinguishable martensite-to-R-phase and R-phase-to-austenite transformations becomes visible (Fig. 4a). This demonstrates a higher sensitivity to changes of the wire shape near the end of the reverse deformation when evaluating curvature changes instead of the lowest wire point. For assessing such an inherent amplification effect, a model system with computer-generated images of artificial wire outlines was analyzed. The artificial wire outlines were set to emulate a reverse deformation from a bent to a straight shape with the lowest point of the wire moving linearly between the images. The images of the artificial wire outline were subject to the different evaluation methods and summarized graphically (Fig. 4b). Whereas the evaluation of the lowest wire point yields a linear reverse deformation curve as expected, the evaluation of curvature yields nonlinear curves which have a smaller slope in the beginning and a larger slope toward the end of the reverse deformation. With the slope of the curve being a measure for the relative deviation from image to image, a larger slope obviously allows for identifying shape changes of the wire at a higher level of detail. Consequently, methods based on the evaluation of curvatures are advantageous when assessing details at the end of the reverse deformation, e.g., for determining R′f and Af temperatures. The disadvantage occurring at the beginning of the reverse deformation can be considered negligible for most applications that usually require knowledge of temperatures at the end of the reverse deformation. For a quantitative assessment of the amplification effect, a temperature range of 15 K at the end of the reverse deformation (− 7.5 to 7.5 °C) of the wire annealed for 5 min was evaluated in detail (Fig. 4a, shaded area). In comparison with evaluation via the lowest point of the wire (Δylp), an increase in the reverse deformation by ~ 15% and ~ 35% is observed when using circle segment fits (Δycs) or second degree polynomial fits (Δysdp), respectively. These values correspond well to the values determined based on the model wires (19 and 37%) in a respective region at the end of the reverse deformation (image number 30 to 40), substantiating the evaluation methods to cause the amplification effect (Fig. 4b, shaded area). Further details regarding the different curvature evaluation methods and the computer-generated wire outlines are discussed in a following section.

Fig. 4
figure 4

(a) Reverse deformation curves of NiTi wire annealed for 5 min. Whereas the curve as determined from the lowest point shows a simultaneous martensite-to-austenite and martensite-to-R-phase-to-austenite transformation, the reverse deformation curves as determined from curvature changes resolve the double-S shape. The dashed lines correspond to the tangents used for determining the transformation temperatures. (b) Reverse deformation curves and select images of the computer-generated model wire. The shaded areas in (a) and (b) indicate the range used for the quantitative assessment of the curvature amplification effect

Full size image

Consistency of Transformation Temperatures Obtained by the Different Evaluation Methods

A comparison of the Af temperatures determined via the different evaluation methods exhibits good agreement within 1 K for all wires with the exception of the lowest point evaluation for the wire annealed for 5 min, as discussed in the previous section. The reverse deformation curves obtained from different evaluation methods show larger deviations at the beginning of the reverse deformation compared to the end of the reverse deformation (Fig. 2). This leads to deviations of approx. 2 K of R′s (5 min and 10 min) and As (30 min). In comparison with repeatability and reproducibility limits of Af and As reported in round robin studies for conventional BFR tests (2.7-13.6 K), the deviations of Af and As reported in this study are small (Ref 6).

The noise when employing curvature evaluation of fourth degree polynomial and ellipse segment fits is highest when analyzing nearly straight wire segments. This noise may especially affect the determination of the Af temperature when an automated routine is employed. However, this can be avoided by using low-noise curvature evaluation methods, e.g., utilizing second degree polynomial fits. In conclusion, the evaluation of curvature change is assessed in the present work as a viable and robust method for determining transformation temperatures in BFR tests.

Analysis of Different Curvature Evaluation Methods with a Model System

In order to further analyze the different fitting methods employed for curvature evaluation, a model system with computer-generated images of wire outlines was analyzed. The artificial wire outlines were again set to emulate a reverse deformation from a bent to a straight shape with the lowest point of the wire moving linearly between the images. The wire outline with the different fits and the corresponding local curvature obtained from the different fits is shown in Fig. 5. The wire is displayed at the beginning (Fig. 5a and b), in the middle (Fig. 5c and d), and close to the end (Fig. 5e and f) of the reverse deformation. As can be seen in Fig. 5(a), (c) and (e), all fitting methods are in good agreement with the wire outline. However, the corresponding local curvatures calculated from the fits with Eq 1 show qualitative differences (Fig. 5b, d, and f). The curvature calculated from a second degree polynomial fit exhibits a maximum in the center of the wire outline and decreases in magnitude with the straightening of the wire. This corresponds well to the experiment, where the center of the wire segment exhibits the highest curvature and the wire straightens out over the course of the experiment, thus decreasing the magnitude of curvature. The curvature calculated from a circle segment fit is constant along the wire outline as expected and also decreases in magnitude for a straightening wire. When analyzing nearly straight wire segments, the curvature calculated from second degree polynomial and circle segment fits is virtually identical (Fig. 5f).

Fig. 5
figure 5

Computer-generated model wire outline with different fitting methods (left column) and corresponding local curvatures calculated with Eq 1 (right column). (a) and (b) Wire at the beginning of the reverse transformation. (c) and (d) Wire in the middle of the reverse transformation. (e) and (f) Wire toward the end of the reverse transformation

Full size image

The curvature calculated from a fourth degree polynomial fit exhibits two inflection points and is largest to the left and right of the lowest wire point (Fig. 5b). These inflection points gradually travel outward with a straightening wire, resulting in a curvature without inflection points and with maxima at the edges for a nearly straight wire (Fig. 5f). This demonstrates that the calculation of the local curvature can introduce complexities even when analyzing seemingly simple curve fits.

The largest differences are observed when calculating the curvature from an ellipse segment fit. The curvature of an ellipse is largest at its vertices, corresponding to curvature maxima at the edges of the wire outline. These maxima increase as the wire is straightening, increasing the magnitude of the curvature averaged over the wire outline instead of decreasing it.

These findings help to explain the different levels of noise as seen when utilizing different curvature evaluation methods. The local curvature as calculated from second degree polynomial and circle segment fits does not show unexpected behavior and thus results in a low level of noise. Using fourth degree polynomials is prone to adapting too strongly to single-pixel variations in the wire outline when analyzing a nearly straight wire. This fact, combined with the aforementioned complexity introduced by the local curvature calculation, causes large curvature changes and thus a higher level of noise. As seen in Fig. 5, the use of ellipse segment fits is inherently prone to extremely large local curvature values at the ellipse vertices. When analyzing experimental data, this effect amplifies slight changes of the wire outline to the point of an unstable reverse deformation curve (Fig. 3).

Even though the curvatures calculated with different evaluation methods may be largely different in their absolute values, the reverse deformation curves generally have a similar shape. Consequently, the transformation temperatures as determined by the tangent method described in ASTM F2082-16 are in good agreement.

Summary

The aim of the present work was to assess potential effects of evaluation methods in non-contact bend and free recovery tests of thin NiTi wires. An according test setup was constructed and successfully applied to thin NiTi wires with diameters as low as 25 µm. Tracking the curvature of wire segments by fitting the wire outline using polynomial, circle, and ellipse segment fit was carried out in order to gain flexibility with respect to shape and positioning of a given sample. In comparison with the usually applied tracking of specific spots, it is shown that tracking curvature changes using second degree polynomial and circle segment fits results in an inherent amplification effect that allows to resolve a two-stage reverse transformation, which was obscured using the conventional method. Aside from this aspect, consistent results regarding the shape of reverse deformation curves and corresponding transformation temperatures were obtained. Tracking curvature changes using fourth degree polynomial and ellipse segment fits was found to result in reverse deformation curves with unsuitably high noise when analyzing nearly straight wire segments. In general, the presented optical evaluation methods were clarified to be robust in producing consistent transformation temperatures within a low margin of 2 K, fitting well in the range observed for repeatability and reproducibility limits of conventional BFR tests.