On the Variation of Hardness Due to Uniaxial and Equi-Biaxial Residual Surface Stresses at Elastic–Plastic Indentation

Abstract

It is established long since that the material hardness is independent of residual stresses at predominantly plastic deformation close to the contact region at indentation. Recently though, it has been shown that when elastic and plastic deformations are of equal magnitude this invariance is lost. For materials such as ceramics and polymers, this will complicate residual stress determination but can also, if properly understood, provide additional important information for performing such a task. Indeed, when the residual stresses are equi-biaxial, the situation is quite well understood, but additional efforts have to be made to understand the mechanical behavior in other loading states. Presently therefore, the variation of hardness, due to residual stresses, is examined at a uniaxial stress state. Correlation with global indentation quantities is analyzed, discussed and compared to corresponding equi-biaxial results. Cone indentation of elastic–perfectly plastic materials is considered.

Introduction

Residual stresses can have a very destructive influence on the load-carrying capacity of engineering structures. The best way to avoid this feature is of course to ensure that such stresses are negligible to start with, but this can in many situations be a difficult task to achieve. Another alternative is to determine such stresses and account for them during the design process. In this context, indentation has been during recent years emerged as a very attractive experimental method for determining residual stresses, especially at smaller length scales.

During the last 20 years or so, there has been a substantial amount of articles dealing with residual stress determination using indentation testing, cf. Ref 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16 (just to mention a few). It could be mentioned here that in Ref 11 indentation testing is in an interesting way combined with so-called hole drilling and inverse analysis to achieve high-accuracy determination of residual stresses. Otherwise, it is of course a rather lengthy task to summarize these findings in detail, but by restricting such a summary to sharp indentation testing of classical elastic–plastic materials the most important overall results are the following:

• At sharp indentation in a situation with dominating plastic deformation, pertinent to most metals and alloys, the hardness H (here and below defined as the average contact pressure) is invariant of residual stresses, and determination of these stresses has to be attempted based on the size of the contact area between the material and the indenter, cf. Ref 1,2,3,4,5.

• Explicit relations for the correlation of residual stresses with the size of the contact area have been presented, cf. Ref 3,4,5, 14, for the case above with dominating plastic deformation. This correlation is relying upon the so-called Johnson parameter (Ref 17, 18) to be discussed in some detail below.

• In a sharp indentation situation where elastic and plastic deformations are of comparable magnitude, pertinent to many ceramics and polymers, the invariance of hardness is lost, cf. Ref 14, 15.

• The variation of hardness can be correlated based on the Johnson parameter (Ref 17, 18), cf Ref 16 at equi-biaxial stress states.

Accordingly, quite a lot of important knowledge has been gained about the mechanics of sharp indentation and residual stresses. In this, most of the results, however, are pertinent to the case of an equi-biaxial residual stress state. This is certainly natural as, for example, stresses due to a distributed temperature often become equi-biaxial. Admittedly, the assumption of equi-biaxiality also simplifies the analysis as, for example, the ratio between principal stresses does not enter the governing equation and axisymmetry of all the field variables can be quietly assumed.

In particular when it comes to the situation with a varying hardness, the case mentioned above where elastic and plastic deformations are of comparable magnitude, very little is known about the effect of a stress state that is not equi-biaxial. It is therefore the intention of the present investigation to remedy this shortcoming.

In doing so, finite element simulations for the case of a uniaxial residual stress state will be performed, and correlation with global indentation quantities is analyzed, discussed and compared to corresponding equi-biaxial results first presented in Ref 16. The investigation is restricted to cone indentation of elastic–perfectly plastic materials, but generality of results, for example, to a contact situation with other indenter geometries and other types of plastic strain hardening can be expected, cf. Ref 4, 5.

Theoretical Background

The theoretical foundation as to a large extent presented in for example (Ref 16) will be used for background. This background includes residual stress determination at rigid-plastic conditions, based on the size of the contact area between the material and the indenter, as well as the new features associated with the loss of hardness invariance in case of indentation where elastic and plastic deformation are of comparable magnitude. In this background section, it is assumed that equi-biaxiality of field variables prevails.

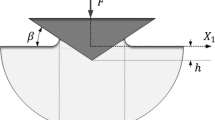
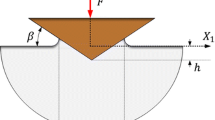
Cone indentation (with an angle β = 22°, same angle as at Vickers indentation), see Fig. 1, of elastic–ideally plastic materials with homogeneous residual equi-biaxial stress fields is then considered. Correlation is sought for based on the non-dimensional strain parameter Λ suggested by Johnson (Ref 17, 18) according to

$$ \varLambda = {{E\tan \beta } \mathord{\left/ {\vphantom {{E\tan \beta } {\left( {\sigma_{y} \left( {1 - \nu^{2} } \right)} \right)}}} \right. \kern-0pt} {\left( {\sigma_{y} \left( {1 - \nu^{2} } \right)} \right)}} $$

(1)

where E, ν, σ_y are Young’s modulus, Poisson’s ratio, initial yield stress, respectively. In Eq 1, only elastic–ideal plasticity is considered, but this limitation can be removed by replacing σ_y with the flow stress at a representative value of the effective plastic strain. Furthermore in 1, β is as indicated in Fig. 1 the angle between the cone indenter and the undeformed surface of the material, see Fig. 1. Based on the Λ-parameter, three levels of contact behavior, see Fig. 2, can then be distinguished. These levels are: level I with almost purely elastic indentation, level II with both elasticity and plasticity being of importance, level III with dominating plasticity. It should be clearly stated that sometimes level III contact behavior is said to prevail when the material hardness H-curve flattens out. In this context however, the specific definition of level III contact is of less interest.

Fig. 1

Schematic of the geometry of cone indentation where a represents the true contact radius. In the present investigation, β = 22°. The nominal contact area A_nom = πh²/(tan β)² where h is the indentation depth

Fig. 2

Normalized hardness, $\bar{H} = {H \mathord{\left/ {\vphantom {H {\sigma_{\text{y}} }}} \right. \kern-0pt} {\sigma_{\text{y}} }}$, and area ratio, c², as functions of ln Λ, defined by Eq 1. Schematic of the correlation of sharp indentation testing of elastic–ideally plastic materials. The three indentation levels I, II and III are also indicated. Approximately, level II contact initiates at Λ = 3 level III contact at Λ = 900. The $\bar{H}$-curve flattens out at (approximately) Λ = 30

At level III conditions, and also at substantial parts of the level II region in Fig. 2, the hardness is, as stated repeatedly above, invariant of residual stresses. The relative contact area,

$$ c^{2} = {A \mathord{\left/ {\vphantom {A {A_{\text{nom}} }}} \right. \kern-0pt} {A_{\text{nom}} }}, $$

(2)

where A (true contact area) and A_nom (nominal contact area) are projected areas, see Fig. 1, and can, however, be related to an equi-biaxial residual stress σ_res according to

$$ c^{2} = c^{2} \left( {\sigma_{\text{res}} = 0} \right) - 0.35\ln \left( {1 + \left( {{{F\sigma_{\text{res}} } \mathord{\left/ {\vphantom {{F\sigma_{\text{res}} } {\sigma_{\text{y}} }}} \right. \kern-0pt} {\sigma_{\text{y}} }}} \right)} \right) $$

(3)

where c²(σ_res = 0) is the value on the relative contact area at indentation of a virgin (unstressed material). This relation was suggested by Rydin and Larsson (Ref 14) based on the equivalence of mechanical fields close to the indenter in case of either contact-induced stresses in an unstressed material or contact-induced stresses in a material with a properly chosen apparent initial yield stress. Consequently, using an apparent yield stress

$$ \sigma_{\text{y,apparent}} = \sigma_{\text{y}} + F\sigma_{\text{res}} $$

(4)

in Λ in Eq 1, according to

$$ \varLambda = {{E\tan \beta } \mathord{\left/ {\vphantom {{E\tan \beta } {\left( {\sigma_{{{\text{y}},{\text{apparent}}}} \left( {1 - \nu^{2} } \right)} \right)}}} \right. \kern-0pt} {\left( {\sigma_{{{\text{y}},{\text{apparent}}}} \left( {1 - \nu^{2} } \right)} \right)}}, $$

(5)

it is possible to rely on a universal c²-curve, as shown schematically in Fig. 2, regardless if residual stresses are present or not. Explicitly this is shown in Fig. 3 where obviously the choice

$$ \begin{aligned} F & = 0.52,\quad \sigma_{\text{res}} < 0 \\ F & = 1.77,\quad \sigma_{\text{res}} > 0, \\ \end{aligned} $$

(6)

suggested in Ref 14 yields results describing a single universal c²-curve with very high accuracy. The different values on F in Eq 6 could be physically explained by the fact that tensile and compressive stresses will have different influences on indentation quantities. Obviously, this universal c²-curve in Fig. 3 can be used to determine σ_res when c²(σ_res = 0) is known.

Fig. 3

Results for equi-biaxial residual stress fields. The area ratio, c², as function of ln Λ, is defined by Eq 5 with the yield stress σ_y replaced by σ_y,apparent in Eq 4. The results are taken from Rydin and Larsson (Ref 12)

When elastic and plastic deformations are of comparable magnitude, the hardness is, as mentioned many times above, no longer invariant of residual stresses. This region of interest, when it comes to Λ-values, is pertinent to the linear variation regime of the normalized hardness, H/σ_y, in Fig. 2. It was recently shown by Larsson (Ref 16) that it is possible to correlate the influence from residual stresses on hardness values in essentially the same way as for the relative contact area c². This correlation is, as for c², based on Eq 4 and 5 and is explicitly shown in Fig. 4, and obviously very good agreement with a universal curve is achieved. It should be noted that the well-known rigid-ideally plastic solution

$$ H = 2.54\sigma_{\text{y}} , $$

(7)

determined experimentally by Atkins and Tabor (Ref 19) is also indicated in Fig. 4. In this context, it should be mentioned that the normalized hardness attains a peak value (overshoot) at the transition zone between level II and level III results. Such a peak value occurs both at sharp indentation, cf. Ref 20, and also at spherical indentation, cf. Ref 21. This feature has not been fully explained in the literature but could possibly be due to remaining effects from elastic deformations at early stages of level III contact behavior.

Fig. 4

Results for equi-biaxial residual stress fields. Normalized hardness, H/σ_y, as function of ln Λ, is defined by Eq 5 with the yield stress σ_y replaced by σ_y,apparent in Eq 4. The straight line represents Eq 7. (White circle), stress-free results taken from Larsson (Ref 17). (Black circle) hardness values taken from (Ref 12) with and without residual stresses. (Asterisk), hardness values taken from (Ref 14) with and without residual stresses

The results in Fig. 4 are pertinent to an equi-biaxial residual stress state, which is an important special case to be expected, for example, at temperature loading of thin film/substrate structures. A more general approach to the problem is of course of substantial interest, and for this reason, the analysis below will also include uniaxial residual, or applied, stress states encountered in a practical situation at for example unidirectional bending.

Numerical Analysis

In this section, the present finite element simulations of the cone indentation problem are described. It is then important to emphasize that due to the fact that uniaxial residual stress states are considered, axisymmetric conditions are lost and a full three-dimensional solution has to be sought for. Similar analyses have been performed previously, for example, in Ref 15), and according to concerning details of the numerical approach, this article is referred to.

Again then, quasi-static cone indentation of elastic–ideally plastic prestressed materials is analyzed here. Frictionless contact is assumed in all simulations. Concerning the constitutive description, the rate-independent Prandtl–Reuss equations for classical Mises plasticity are relied upon accounting for large deformations. Ideally plastic conditions are assumed, and accordingly plastic deformation is initiated and maintained when the Mises effective stress

$$ \sigma_{\text{e}} = \sigma_{\text{y}} . $$

(8)

When elastic loading, or unloading, is at issue, a hypoelastic formulation in Hooke’s law is used.

The material hardness is, as stated above, defined as the average contact pressure during loading according to

$$ H = {F \mathord{\left/ {\vphantom {F A}} \right. \kern-0pt} A} $$

(9)

where F is the indentation load and A is the projected contact area. In this context, it should be mentioned that if the residual stresses are homogeneous as assumed presently, the problem is self-similar with no characteristic length, and as a result global indentation properties, such as hardness and relative contact area, are independent of indentation depth.

A schematic picture of the surface residual stresses, with the contact area between indenter and material indicated, is shown in Fig. 5. In the case of most interest presently, uniaxial residual stresses is,

$$ \sigma_{1} = \sigma_{\text{res}} ,\quad \sigma_{2} = 0 $$

(10)

while

$$ \sigma_{1} = \sigma_{2} = \sigma_{\text{res}} $$

(11)

corresponds to the previously analyzed case of equi-biaxial residual stresses. For a general stress state, the contact area will become ellipsoidal, a₁ ≠ a₂, while in the simpler equi-biaxial case a₁ = a₂. Accordingly, a three-dimensional finite element analysis is required at uniaxial residual loading.

Fig. 5

Schematic of the contact area (shaded) at indentation. The principal residual stresses and also the corresponding semi-axes of the elliptical contact area are indicated

The boundary value problem schematically outlined above was solved using the multi-purpose finite element program ABAQUS (Ref 22). Approximately 100,000 eight-node hybrid solid elements were used to discretize the material, while the conical indenter was assumed to be rigid. Due to existing symmetries, only one-quarter of the material needs to be modeled. The resulting finite element mesh is shown in Fig. 6, where for clarity only the mesh details close to the contact region are shown. Residual (applied) stresses are enforced by prescribed boundary displacements prior to indentation. Note that no distinction is made between residual and applied stresses in this analysis. The applied prestresses are kept within the elastic limit.

Fig. 6

Finite element mesh, close to the region of contact, used in the numerical simulations. The coordinate Y corresponds to X₂ in Fig. 1

Results and Discussion

In this section, the present finite element results pertinent to uniaxial residual stresses are presented, discussed and compared to corresponding equi-biaxial results. The present results are derived for the case

$$ \ln \varLambda = 3.4 $$

(12)

where especially the Johnson (Ref 17, 18) parameter Λ is given by Eq 1. This value was chosen to ensure that the stress-free material experienced level III contact (the material hardness is given by Eq 7), while the behavior entered the level II regime in the presence of tensile stresses. This is based on the result for the equi-biaxial case that ln Λ = 3 constitute an approximate border between level II and level III indentations (with Λ defined according to Eq 4 and 5), and a clear hardness dependence at higher tensile stresses (lower values on Λ when accounting for the change in yield stress), cf. Ref 16 and Fig. 4. Concerning residual stresses, the values

$$ \left( {{{\sigma_{\text{res}} } \mathord{\left/ {\vphantom {{\sigma_{\text{res}} } {\sigma_{\text{y}} }}} \right. \kern-0pt} {\sigma_{\text{y}} }}} \right) = - 1.0, - 0.75, - 0.5, - 0.25,0,0.25,0.5,0.75,1.0 $$

(13)

were investigated.

It should be emphasized that compressive stresses will increase Λ, when again defined according to Eq 4 and 5, leading to a more pronounced level III (rigid-plastic) situation pertinent to the material hardness, which is not of direct interest presently. However, compressive residual stresses are included in the analysis for clarity and of course also to analyze the hardness invariance at ln Λ > 3, approximately (Λ defined according to Eq 4 and 5).

Before presenting explicit results, it should also be mentioned that in the present situation a direct comparison between uniaxial and equi-biaxial results is rather straightforward based on the Mises effective stress σ_e. In short, this is due to the fact that the value on the effective stress σ_e is the same (σ_e = σ_res) for both the residual stress systems in 10 and 11. (Obviously this refers to a situation prior to indentation.) Clearly, since surface residual stresses are at issue, the principal stress σ₃ = 0.

The explicit results based on 12 and 13 are now shown in Fig. 7 where the non-dimensional hardness is depicted as function of the stress ratio (σ_res/σ_y). Clearly, as could be expected from the equi-biaxial results there is a clear stress dependence in particular for the case of tensile residual stresses. For compressive stresses, the dependence (deviation from rigid-plastic contact behavior) is essentially within the numerical accuracy. For example, when (σ_res/σ_y) takes on the extreme value − 1.0 the hardness increases with only 2%. It should also be noted, as will be discussed in more detail below, that the stress dependence is less pronounced in the present uniaxial case as compared to the equi-biaxial case investigated in detail in Larsson (Ref 16).

Fig. 7

Results for uniaxial residual stress fields. Non-dimensionalized hardness, H/H ₀ , as function of residual stress ratio, σ_res/σ_y. (Dashed line) H/H ₀  = 1. (White circle) presents numerical results

The latter feature is of course of substantial importance when it comes to determination of residual stresses in a practical case. For this reason, this is examined in more detail in Fig. 8 where results for both the uniaxial and the equi-biaxial cases are shown. Since obviously tensile stresses are of most importance, only results for positive values in 13 are depicted. It is very clear from what is shown in Fig. 8 that the hardness is far more influenced by an equi-biaxial residual stress σ_res than a corresponding uniaxial one. For example, at (σ_res/σ_y) = 1, the hardness value is reduced (compared to the stress-free hardness) with around 18% in the equi-biaxial case but with only approximately 6% in the uniaxial one. In practice, it would be very hard if not impossible experimentally to accurately determine σ_res based on such a small variation from the stress-free results.

Fig. 8

Non-dimensionalized hardness, H/H ₀ , as function of residual stress ratio, σ_res/σ_y. (Dashed line) H/H ₀  = 1. (White circle) presents numerical results for uniaxial residual stresses. (Black circle) results from (Ref 14) for equi-biaxial residual stresses

Despite this rather disappointing result, it is still of interest to investigate whether the uniaxial case can be correlated with the Johnson (Ref 17, 18) parameter Λ when defined by Eq 4 and 5. This is so remembering that such a correlation could be advantageous for determination of stress fields lying between uniaxial and biaxial (where in the latter case the influence on the material hardness is more pronounced). In Fig. 9 then the uniaxial stress results in Fig. 7 are plotted against ln Λ in the same manner as in Fig. 4. For clarity of the presentation, the behavior of the stress-free and equi-biaxial results in Fig. 4, in the approximate range 2 < ln Λ < 3.5, is represented by a straight thick line. Two important results can be immediately noted from this figure. First of all, as already stated above and shown in Fig. 8, the influence from residual stresses on the hardness values is noticeably smaller in the uniaxial case than in the equi-biaxial case (also when expressed by the Johnson (Ref 17, 18) parameter Λ). Secondly, correlation with a universal curve cannot be expected to give good accuracy.

Fig. 9

Normalized hardness, H/σ_y, as function of ln Λ, is defined by Eq 5 with the yield stress σ_y replaced by σ_y,apparent in Eq 4. The straight horizontal line represents Eq 7. The straight thick line represents the stress-free and equi-biaxial results in Fig. 4 in the approximate range 2 < ln Λ < 3.5. (White circle) presents numerical results for uniaxial residual stresses

To summarize the results presented in Fig. 7, 8 and 9, it can be concluded that when residual stresses are uniaxial the hardness variation is not an appropriate feature for stress determination. In this context, it should be mentioned, however, that it has been shown previously that this can be achieved using the relative contact area c², cf. Ref 23 where also correlation with the Johnson (Ref 17, 18) parameter Λ is confirmed. Without going into details, the reason for this is essentially that c² is much more sensitive to the uniaxial stresses (elastic deformation) than the material hardness.

Having said this it is certainly of significant interest to discuss alternatives to the present approach. While the major advantage with the method at issue is simplicity (residual stresses can be explicitly determined from a single simple relation), the limited variation of the hardness due to residual stresses (in particular then in the presently investigated uniaxial case) makes it impossible to achieve acceptable accuracy at determination of such quantities. An attractive and more advanced alternative in such a case could be to rely on indentation experiments in combination with inverse analysis (Ref 9,10,11). This can be particularly advantageous if indentation is combined with other standard methods for residual stress determination such as hole drilling (Ref 11). Inverse modeling will, however, require substantial efforts but ways to handle this issue have been presented in for example (Ref 24).

There are of course also important features that are not included in the present theory. Such features include, for example, indentation creep (Ref 25), scale effects (Ref 26) and influence from the substrate at thin film characterization (Ref 27). Indentation creep concerns the constitutive behavior of the material and cannot be accounted for without another material description and also properly determining creep material quantities. The other effects can, however, be minimized by an appropriate choice on the value of the indentation depth h. Another feature that is not included in this analysis is any possible effect from the residual stresses on the material properties. This is certainly a very interesting issue and could, for example, be addressed by incorporating the relevant results by Ma et al. (Ref 28) into the present approach for residual stress determination. Such a matter is, however, left for future considerations.

As a final comment, it should be emphasized that the present results have bearing also for other types of contact problems. In particular, this is related to scratching and scratch testing, where correlation using the Johnson (Ref 17, 18) parameter Λ also is a major issue, cf. Ref 29,30,31,32,33, but also material characterization by inverse modeling, cf. Ref 34 and using hardness testing to analyze multi-fields, cf. Ref 35.

Conclusions

The effect from uniaxial residual stresses on the material hardness is analyzed, discussed and compared to corresponding results for equi-biaxial residual stresses. The analysis is restricted to cone indentation of elastic–ideally plastic materials. The most important findings can be summarized as follows:

• The material hardness is much less influenced by uniaxial residual stresses than by corresponding equi-biaxial ones.

• Correlation with the Johnson (Ref 17, 18) parameter Λ is not accurate in case of uniaxial residual stresses. In the equi-biaxial case, such correlation can produce a universal curve together with stress-free hardness results.

• From a practical point of view, the hardness variation is not an appropriate quantity to be used experimentally for uniaxial residual stress determination in, for example, ceramics and polymers. A better alternative for this purpose is to use the relative contact area, here denoted c².