Effects of Dy₂O₃ on the Electrical Properties of a (Nb₂O₅-Dy₂O₃-SiO₂) Co-doped TiO₂ Varistor

Abstract

Rutile-TiO₂ ceramics are very promising electronic ceramic materials which can be applied in varistors because of their good electrical properties. In this work, Dy₂O₃ was used to improve the electrical properties of a TiO₂ varistor doped with 0.60 mol.% Nb₂O₅ and 0.30 mol.% SiO₂. Results showed that the TiO₂ varistor doped with 0.30 mol.% Dy₂O₃ possessed optimal electrical properties with good nonlinear coefficient ($\alpha = 5.7$), very low breakdown voltage ($E_{\text{B}} = 1.34\;{\text{V}}\,{\text{mm}}^{ - 1}$) and colossal dielectric constant ($\varepsilon_{\text{r}} = 8.01 \times 10^{5}$). The microstructural analysis showed that after the incorporation of Dy₂O₃ into the TiO₂ varistor, the grains tended to be more semiconducting due to the defect carriers derived from the substitution of Dy³⁺ for Ti⁴⁺. Meanwhile, the moderate dopant of Dy₂O₃ also increased the grain size and narrow grain boundary. Consequently, the breakdown voltage decreased, while the nonlinear coefficient and dielectric constant improved.

Introduction

Titanium dioxide ceramic is a kind of electronic ceramic that can attain good nonlinear electrical properties and dielectric constant by special methods, which makes it of great interest for a broad application concerning varistors and capacitors. In the past, the ZnO varistor was most widely used owing to its excellent nonlinear characteristics.1 However, the ZnO varistor cannot be applied in low-voltage electronic circuits because of its high breakdown voltage.2 In recent years, with the miniaturization and integration of electronic circuits, it is necessary to develop multifunctional varistors with low breakdown voltage.3,4,5 As one of the typical electronic ceramics with multifunction, the TiO₂ varistor has attracted extensive attention due to its low breakdown voltage and good dielectric properties. However, the application of the TiO₂ varistor is limited by its low nonlinear coefficient and relatively high breakdown voltage for electronic circuits.

In theory, the breakdown voltage and nonlinear coefficient of the TiO₂ varistor mainly depend on the potential barrier and the grain size of TiO₂ ceramics.1,6,7 In order to improve the nonlinear electrical properties of TiO₂ ceramics, most researchers concentrated on donor doping (Nb⁵⁺,Ta⁵⁺) and acceptor doping (Ho³⁺,Cr³⁺).8,9 In addition, the influences of sintering temperature and heat treatment atmosphere on the electrical properties of the TiO₂ ceramic were also studied.10,11,12 In 1995, Yan and Wu found that doping 0.25 at.% Nb⁵⁺ was beneficial to the varistor properties of (Ba-Bi-Nb)-doped TiO₂.13 Meanwhile, Luo et al. reported that Ta₂O₅ could effectively improve the properties of (Ca, Si, Ta)-doped TiO₂ varistor.14 These two reports confirmed that donor doping could effectively enhance the varistor properties of TiO₂ ceramics, but the high breakdown voltage still limited its application. Sousa et al. investigated the effect of Ta₂O₅ as well as Cr₂O₃ on the varistor properties of TiO₂ 9 and Kang et al. reported the (Ge, GeO₂, Ta₂O₅, BaCO₃) co-doped TiO₂ varistor with an α value up to 12.1 and a low breakdown voltage of 20.8 V/mm.15 Although both donor doping and acceptor doping were shown helpful to the electrical properties of the TiO₂ varistor, the difficulties of coordinating the breakdown voltage and nonlinear coefficient, i.e., how to further reduce the breakdown voltage and enhance the nonlinear coefficient simultaneously, has become a challenge for researchers. In addition, heat treatment atmospheres also had a favorable effect on TiO₂ varistor properties. For instance, Zhao et al. implied that after the TiO₂ varistor was heat-treated in oxygen atmosphere, the acceptor state density as well as the height and width of the potential barriers increased, the conductivity decreased and the breakdown voltage rose significantly as a consequence of oxygen accumulation at grain boundaries.10

Previous studies on TiO₂ ceramics mainly focused on the improvement of nonlinear properties. However, recently, researchers found that the doping of In³⁺ + Nb⁵⁺ (1:1) into TiO₂ ceramics (INTO) produced colossal dielectric properties, making the TiO₂ ceramics a potential capacitor.16 Subsequently, Thongbai et al. reported the effects of sintering conditions and doping concentrations on Sc³⁺ + Nb⁵⁺ (1:1) co-doped TiO₂ ceramics and found that Sc³⁺ captured free electrons at internal insulating layers while Nb⁵⁺ produced free electrons. The work revealed that the interfacial polarization at insulating layers and large activation energy contributed to colossal dielectric properties of ScNTO ceramics.17 Lately, there has been much research about Eu³⁺ + Nb⁵⁺,18 La³⁺ + Ta⁵⁺,19 Er³⁺ + Ta⁵⁺,20 Bi³⁺ + Eu³⁺ + Nb⁵⁺,21 B³⁺ + Eu³⁺ + Nb⁵⁺22 co-doped rutile TiO₂ ceramics with high dielectric constant and low dielectric loss. Admittedly, the dielectric properties of TiO₂ ceramics have been greatly improved in a short time.23,24,25,26 However, with the integration and multifunction of electronic circuits, multifunctional TiO₂ ceramics are drawing increasing intention. To the best of our knowledge, there are few works reporting both the nonlinear characteristic and dielectric properties of TiO₂ varistors.

It has been confirmed that SiO₂ controls the grain size of the varistor while acceptor doping improves the varistor properties of TiO₂ ceramic.6,27 Herein, this work reported that (0.30Dy₂O₃-0.60Nb₂O₅-0.30SiO₂-98.80TiO₂) (mol.%) co-doped TiO₂ ceramic systems with low breakdown voltage, high nonlinear coefficient and colossal dielectric constant were procured via optimizing sintering temperature and doping concentrations of Dy₂O₃. The dependence of electrical properties on microstructure was thoroughly investigated and a defect model was proposed to illustrate the effects of Dy₂O₃ on the properties of the TiO₂ varistor.

Experimental Details

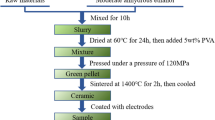
TiO₂ ceramic samples (99.10-x)TiO₂-xDy₂O₃-0.60Nb₂O₅-0.30SiO₂ (mol.%, x = 0, 0.15, 0.30, 0.45, 0.60) were prepared by the conventional solid state sintering method. The raw materials TiO₂ (99.9%), SiO₂ (99.9%), Dy₂O₃ (99.99%) and Nb₂O₅ (99.99%) were purchased from Chengdu Chron Chemicals Co., Ltd., China. A total of 0.18 mol chemicals were weighed in stoichiometric proportions and milled in a planetary ball mill for 12 h using 100 mL ethanol as the medium. After drying at 70°C for 18 h, the homogeneous powder mixture was blended with a small amount of PVA (polyvinyl alcohol) solution (PVA/H₂O = 8 wt.%). Afterwards, the mixed powder was pressed at 120 MPa into pellets of 15 mm in diameter and 2 mm in thickness. Next, all the pellets were sintered at a designed temperature (1350°C, 1400°C, 1450°C) for 2 h and cooled to room temperature in furnace. To characterize the varistor and dielectric properties of the sintered tablets, both the surfaces were polished and then deposited with silver electrodes, followed by heat treatment at 600°C for 1 h. The varistor properties, including nonlinear coefficient (α) and breakdown voltage (E_1mA), were measured by a varistor DC parameter instrument (CJ1001). The dielectric constant, dielectric loss at 1 kHz and the dielectric properties measurements dependent on temperature were conducted over the range of − 150–200°C at a heating rate of 1°C min⁻¹ by an LCR meter (TH2816A). The dielectric properties of samples in the frequency range of 100 Hz–100 kHz were measured by an impedance analyzer (Agilent 4294A) at room temperature. The true density of TiO₂ ceramics was estimated by a density meter (ET-320) based on the Archimedes method and the relative density was calculated by the true density and theoretical density accordingly. The crystal structure of TiO₂ ceramic samples was determined by an x-ray diffractometer (XRD) (DX-2000) with Cu Kα radiation at a scanning speed of 0.04° s⁻¹ in the 20°–80° 2θ range. After polishing and thermally etching, the surface of TiO₂ ceramic samples was observed by scanning electron microscopy (SEM, JSP 7500, Japan). The average grain size is calculated by the intercept method proposed by Mendelson9:

$$ D = \frac{1.56L}{MN} $$

(1)

where L is the length of a random line on the SEM image, M is the magnification of the SEM image and N is the number of grain boundaries that the line crosses.

Energy-dispersive x-ray spectroscopy (EDS) was used to analyze the elemental composition and distribution. The valence state of elements in TiO₂ samples was tested by x-ray photoelectron spectroscopy (XPS, Kratos AXIS Ultra DLD, Japan).

Results and Discussion

Nonlinear Characteristics

Table I presents the electrical performances of TiO₂ ceramics doped with Dy₂O₃ at different sintering temperatures. When the sintering temperature increases, the nonlinear coefficient and dielectric constant increase, while breakdown voltage and dielectric loss decrease. Altogether, it is observed that the samples possess the best varistor properties after sintering at 1450°C. This phenomenon may be explained by the following equations:

$$ {\text{Nb}}_{2} {\text{O}}_{5} + 2{\text{TiO}}_{2} \xrightarrow{{{\text{TiO}}_{2} }}2{\text{Ti}}_{{{\text{Ti}}}}^{\prime } + 2{\text{Nb}}_{{{\text{Ti}}}}^{.} + 8{\text{O}}_{{\text{o}}} + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}{\text{O}}_{2} $$

(2)

$$ E_{\text{B}} = NV_{\text{gb}} $$

(3)

where $E_{\text{B}}$ is the breakdown voltage, $N$ is the number of grains per unit length, $V_{\text{gb}}$ is the voltage barrier at the grain boundary.

Table I Electrical properties of different TiO₂ samples. (E_1mA/V mm⁻¹; $\varepsilon_{\text{r}}$/× 10⁵; 1 kHz)

According to the above equations, the titanium ion defects can be generated by the dopant of Nb₂O₅ and the breakdown voltage is determined by the grain size. Increasing the sintering temperature can improve the solubility of Nb₂O₅, so the ion segregation at the grain boundary is moderated. In this case, more Nb⁵⁺ ions replace Ti⁴⁺ ions and the resulting ion defects promote the degree of semiconducting of the grains. In addition, the grains grow as the sintering temperature rises, leading to the enhancement of grain boundary barriers and a decrease of grain boundaries per unit thickness.8,12 As a consequence, α increases while $E_{\text{B}}$ decreases. Throughout this work, we, therefore, picked 1450°C as the sintering temperature for all the Dy₂O₃-doped samples.

After sintering at 1450°C, the breakdown voltage and nonlinear coefficient of different samples are depicted in Fig. 1a, and the other parameters of samples with different x values are listed in Table II. $\varPhi_{\text{B}}$ is calculated by the following equations:

$$ J = A * T^{2} \exp \left( {\frac{{\beta E^{1/2} - \varPhi_{\text{B}} }}{kT}} \right) $$

(4)

$$ \ln J = \frac{\beta }{kT} E^{1/2} + \ln A * T^{2} - \frac{{\varPhi_{\text{B}} }}{kT} $$

(5)

where A* is the Richardson constant, K is the Bolzmann constant, T is the absolute temperature, $\varPhi_{\text{B}}$ is the interface barrier height, and β refers to the relationship illustrated in Eq. 6:

$$ \beta = \left[ {\left( {\frac{1}{d\omega }} \right)\left( {\frac{{2e^{3} }}{{4\pi \varepsilon_{0 } \varepsilon_{\text{r}} }}} \right)} \right]^{1/2} $$

(6)

where d is the number of grains per unit length, e is the electron charge (1.602 × 10⁻¹⁹ C), $\varepsilon_{0}$ is the vacuum dielectric constant (8.85 × 10⁻¹⁴ F/cm), and $\varepsilon_{\text{r}}$ is the dielectric constant of TiO₂ ceramic. Table II and Fig. 1a show that the doping of Dy₂O₃ obviously affect the properties and microstructure of Nb₂O₅-SiO₂-TiO₂ ceramics. Compared to the sample without Dy₂O₃, all those doped with Dy₂O₃ possess lower breakdown voltage and higher relative density. The doped Dy₂O₃ also greatly enhances the dielectric constant without increasing the dielectric loss significantly. In addition, an appropriate doping content of Dy₂O₃ can improve the nonlinear coefficient of TiO₂ ceramics. When the TiO₂ varistor is doped with 0.30 mol.% Dy₂O₃, the breakdown voltage decreases to 1.34 V mm⁻¹, α ascends to 5.7, and the dielectric properties ($\varepsilon_{\text{r}}$ = 8.01 × 10⁵, $\tan \delta$ = 0.362) and relative density are optimal (98.22%). However, when doped with excessive Dy₂O₃ (x > 0.30), the electrical properties of Nb₂O₅-SiO₂-TiO₂ ceramics deteriorate. Figure 1b shows that the doping content of Dy₂O₃ also exerts an evident influence on the J–E characteristics. The curves can be divided into two regions: one is a low-current linear region (J < 0.03 mA cm⁻²), the other is a nonlinear region.13 The contrast of curves of the Dy₂O₃-doped samples and the undoped one shows that Dy₂O₃ can efficiently reduce the breakdown voltage of TiO₂ ceramics. In sum, the doping of Dy₂O₃ remarkably ameliorates the α and $E_{\text{B}}$ of TiO₂ ceramics, while modifying the concentration of Dy₂O₃ only makes a noticeable contribution to the former. Consequently, Nb₂O₅-SiO₂-TiO₂ ceramics doped with 0.30 mol.% Dy₂O₃ demonstrates the optimum varistor properties.

Fig. 1

Varistor properties of Dy₂O₃-doped TiO₂ ceramics sintered at 1450°C: (a) correlations of breakdown voltage ($E_{\text{B}}$) and nonlinear coefficient (α) with Dy₂O₃ content; (b) dependence of J–E characteristics curve on Dy₂O₃ content.

Table II Characteristic parameters of TiO₂ ceramics doped with Dy₂O₃ sintered at 1450°C

The classical defect reaction equation can be used to understand how Dy₂O₃ influences the electrical properties of Nb₂O₅-SiO₂-TiO₂ ceramics. To start with, the radius of Dy³⁺ (0.091 nm) is much larger than that of Ti⁴⁺ (0.061 nm), which causes severe lattice distortion and leads to the poor solubility of Dy³⁺ in TiO₂ lattice, thus most of the Dy³⁺ ions segregate at the grain boundary.8,28 Furthermore, the dissolution of Dy₂O₃ into TiO₂ lattice also induces oxygen vacancies for charge transfer when Dy³⁺ substitutes for Ti⁴⁺, as shown in Eq. 7 below.

$$ {\text{Dy}}_{2} {\text{O}}_{3} \mathop{\longrightarrow}\limits{{{\text{TiO}}_{2} }}2{\text{Dy}}_{\text{Ti}}^{\prime } + {\text{V}}_{\text{O}}^{..} + 3{\text{O}}_{\text{O}} $$

(7)

When a moderate content of Dy₂O₃ is doped in the TiO₂ varistor, on the one hand, some of the dopant dissolves in the TiO₂ lattice to generate oxygen vacancies, and on the other hand, the remaining Dy³⁺ ions segregate at the grain boundary to form the secondary phase. Consequently, the electrical properties are improved. Nonetheless, if the dopant of Dy₂O₃ is excessive, more quantities of the secondary phase will be generated by consuming a large number of Dy³⁺ ions at grain boundary, which decreases the acceptor interface state density at the depletion layer. The final outcome is a decrease in the height of the grain boundary barrier, which can be explained by Eq. 829:

$$ \varPhi_{\text{B}} = e^{2} N_{\text{S}}^{2} /\left( {2\varepsilon_{\text{r}} \varepsilon_{0} N_{\text{D}} } \right) $$

(8)

where N_S is the acceptor interface state density, $\varepsilon_{\text{r}}$ is the dielectric constant, $\varepsilon_{0}$ is the dielectric constant of vacuum and N_D is the donor content in the depletion layer. According to Eq. 8, the height of the grain boundary barrier $\varPhi_{\text{B}}$ is proportional to the acceptor interface state density.

Dielectric Properties

Figure 2 shows the dielectric properties of Nb₂O₅-Dy₂O₃-SiO₂ co-doped TiO₂ ceramics at room temperature in the frequency range of 10²–10⁵ Hz. It can be seen from Fig. 2 that the dielectric constant and dielectric loss are nearly steady in the frequency range of 10²–10³ Hz. However, with the increase of frequency ($> 10^{3}$ Hz), the dielectric constant decreases while the dielectric loss increases obviously. In addition, when 0.30 mol.% Dy₂O₃ is added into the TiO₂ varistor, the best comprehensive dielectric properties can be obtained at the frequency of 100 Hz, where the dielectric constant is higher than 10⁶ and the dielectric loss is lower than 0.3. Furthermore, in the frequency range of 10²–10⁵ Hz, the dielectric constant (> 1 × 10⁵) of the TiO₂ samples is much better than the previously reported results.19,21,22,30,31 However, the dielectric loss is still higher than other reports, which makes it necessary to further reduce its dielectric loss for capacitor applications.

Fig. 2

Dielectric properties of Dy₂O₃-doped TiO₂ varistor in the frequency range of 10²–10⁵ Hz, measured at room temperature: (a) dielectric constant; (b) dielectric loss.

Figure 3 shows the dielectric properties of Nb₂O₅-Dy₂O₃-SiO₂ co-doped TiO₂ ceramics at different temperatures measured at 100, 1k, 10k and 100k Hz respectively. It can be seen that the dielectric constant and dielectric loss remain relatively stable over − 150–200°C temperature range at different frequencies, except for an expanded dielectric relaxation around 0°C, which may be caused by electron hopping between Ti⁴⁺ and Ti³⁺.32 In summary, it can be concluded from Figs. 2 and 3 and Table I that 0.30 mol.% Dy₂O₃-doped TiO₂ ceramic possesses the best dielectric properties, with the highest dielectric constant, lower dielectric loss, relatively higher frequency stability.

Fig. 3

The dielectric constant ($\varepsilon_{\text{r}}$) (a) and dielectric loss ($\tan \delta$) (b) of Dy₂O₃ doped TiO₂ varistor at different temperatures measured at 100, 1k, 10k and 100k Hz.

XRD Analysis

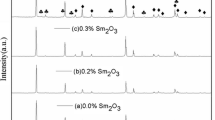
The XRD patterns of TiO₂ ceramics doped with different contents of Dy₂O₃ are exhibited in Fig. 4. Figure 4a demonstrates that only one major phase corresponds to rutile TiO₂ (PDF#87-0710) in all the samples. Meanwhile, as the concentration of Dy₂O₃ increases, the secondary phase Dy₂Ti₂O₇ (PDF#17-0453) appears. Figure 4b is the enlarged partial spectra of Fig. 4a around $2\theta = 27.5^{^\circ }$. It can be seen that after Dy₂O₃ is doped in, the peaks around $27.5^{^\circ }$ shift to a larger angle and their full width at half maximum (FWHM) widens, while increasing the content of Dy₂O₃ dopant makes little difference to the shifting. Basically, the dissolution of Dy³⁺ in the TiO₂ lattice results in severe lattice distortion, thereby decreasing the interplanar spacing value. According to the Bragg formula (9), the angle $\theta$ shifts to the large-angle direction if the interplanar spacing value $d$ decreases.15

Fig. 4

The XRD patterns of different TiO₂ samples sintered at 1450°C (a) and the enlarged partial spectra around $2\theta = 27.5^{^\circ }$ (b).

$$ \lambda = 2d\sin \theta $$

(9)

where λ is the wavelength of the x-ray, $d$ is the interplanar distance, $\theta$ is the angle between the incident wave and the crystal plane. Since the solid solubility of Dy³⁺ in the TiO₂ lattice is low, the undissolved Dy³⁺ ions diffuses to the grain boundary, which is beneficial to the increase of the width of depletion layers and the enhancement of grain boundary potential barrier; therefore, the nonlinear coefficient increases based on the following formula5:

$$ \alpha = \frac{\gamma }{E}\varPhi_{\text{B}}^{3/2} $$

(10)

where $\gamma$ is a constant, E is the external electric field, $\varPhi_{\text{B}}$ is the potential barrier height. Additionally, the segregation of Dy³⁺ ions along the grain boundary also produces a secondary phase Dy₂Ti₂O₇.

SEM Analysis

Figure 5 illustrates the SEM images and grain size of different TiO₂ ceramic samples. The microstructures show that after Dy₂O₃ is doped in, the grain size increases, the grain boundary is narrowed and the secondary phase is evenly distributed at the grain boundary initially. Furthermore, as more Dy₂O₃ is doped, more secondary phase particles are observed. Noticeably, the grain size reaches a maximum of 18.56 μm at x = 0.30 and tends to diminish with the continuous addition of Dy₂O₃. This phenomenon can be explained as follows: when moderate Dy₂O₃ is added, oxygen vacancies are generated due to the substitution of Dy³⁺ ions for Ti⁴⁺ ions, which change the oxygen pressure in rutile TiO_2.33 Therefore, the dopant of Dy₂O₃ promotes the growth of grains.8,33 According to Eq. 3, the breakdown voltage (E_B) decreases greatly. In addition, the moderate secondary phase can also enhance the dielectric properties due to their high resistance.34 However, the deposition of excessive secondary phase (x > 0.30) at the grain boundary can limit the grain growth. Accordingly, E_B increases as a result of the decreasing of grain size. Moreover, by consuming a large number of Dy³⁺ and Nb⁵⁺ ions, the formation of an inordinate secondary phase reduces the acceptor interface state density at the depletion layer, thus causing the nonlinear coefficient to drop according to Eq. 8.

Fig. 5

SEM images and grain size of TiO₂ samples doped with different contents of Dy₂O₃.

EDS Analysis

To further analyze the elemental distribution and explore the effect of Dy₂O₃ on the microstructure, the EDS analysis of TiO₂ ceramics doped with different contents of Dy₂O₃ is conducted. Figure 6 shows the point scanning spectra of EDS for samples x = 0 and x = 0.30, respectively, and the corresponding elemental composition is listed in Tables III and IV. Figure 6a and b shows that a small amount Si exists in the grain of both samples. Meanwhile, Fig. 6b and c depicts the difference in elemental composition between the grain and the gain boundary of the 0.30 mol.% Dy₂O₃-doped sample. Particularly, there exists a very small amount of Dy (~ 0.04%) in the grain, whereas the grain boundary is enriched with a large amount of Dy, Si, Nb in the form of the secondary phase. A reasonable explanation for the phenomenon is that since both radii of Si⁴⁺ (0.040 nm) and Dy³⁺ (0.091 nm) ions differ markedly from the radius of Ti⁴⁺ (0.061 nm) ions, the solubility of Si⁴⁺ and Dy³⁺ in TiO₂ lattice is low, resulting in the segregation of a large amount of Si⁴⁺ and Dy³⁺ at the grain boundary. Altogether, EDS analysis and the aforementioned XRD detection leads to the conclusion that the stable secondary phase at the grain boundary is Dy₂Ti₂O₇.

Fig. 6

The point scanning spectra of EDS for samples x = 0 and x = 0.30: (a) grain of x = 0; (b) grain of x = 0.30; (c) grain boundary of x = 0.30.

Table III The elemental composition of the TiO₂ ceramics sample x = 0

Table IV The elemental composition of the TiO₂ ceramics sample x = 0.30

Figure 7 shows the elemental mapping of TiO₂ ceramics doped with 0 mol.%, 0.30 mol.% as well as 0.60 mol.% Dy₂O₃ , respectively. It can be seen from Fig. 7a that for the undoped TiO₂ varistor, all elements except for Si are evenly distributed in the grain and at the grain boundary, which is consistent with the EDS point analysis. When Dy₂O₃ is added to the TiO₂ varistor, however, the elements Nb, Dy, Si and O are enriched at the grain boundary and the enrichment becomes more obvious with the doping content increasing to 0.60 mol.%. The observation suggests that the doping of Dy₂O₃ notably changes the elemental distribution of Si and Nb. Normally, the segregated elements are involved in the formation of depletion layers. Nevertheless, there is a secondary phase once the accumulated Nb⁵⁺ and Si⁴⁺ exceed the saturation value.6,28

Fig. 7

The elemental mapping of TiO₂ ceramics (a) x = 0, (b) x = 0.3 and (c) x = 0.60.

Figure 8 depicts the line scanning spectra of EDS for Dy₂O₃-free and 0.30 mol% Dy₂O₃-doped TiO₂ samples, respectively. As presented in Fig. 8a, the elemental content of Nb and Ti displays no conspicuous variation within the scanning distance, while the content of Si and O fluctuates apparently between the interior and boundary of grain. However, remarkable fluctuations emerge in all the EDS spectra for 0.30 mol% Dy₂O₃-doped sample at the grain boundary as illustrated in Fig. 8b. These findings are consistent with the results of elemental mapping analysis. Moreover, the grain boundary width can be estimated according to the abrupt variation in the EDS spectra, which turns out to be about 600 nm for the Dy₂O₃-free sample and approximately 400 nm for the 0.30 mol.% Dy₂O₃-doped sample, separately. Therefore, the doping of Dy₂O₃ can also narrow the grain boundary, thereby increasing the density of TiO₂ ceramics. In other words, the moderate dopant of Dy₂O₃ promotes grain growth, narrows the grain boundary and increases the density of TiO₂ ceramics, leading to the decrease of grain boundaries per unit thickness. According to Eq. 2, the breakdown voltage decreases.

Fig. 8

The line scanning spectra of EDS for TiO₂ ceramic samples x = 0 (a) and x = 0.30 (b).

XPS Analysis

To investigate the corresponding chemical valance states of the TiO₂ ceramic sample doped with 0.30 mol.% Dy₂O₃, XPS analysis is conducted and the results are shown in Fig. 9. It was reported that the dopant of electron-donors such as Nb⁵⁺ or Ta⁵⁺ generate free electrons in rutile-TiO₂ ceramics.17 According to Eqs. 2 and 11, Ti³⁺ ions is produced by Ti⁴⁺ ions capturing free electrons.

Fig. 9

XPS spectra of different elements, including (a) Ti, (b) O, (c) Nb, (d) Dy and (e) Si of the TiO₂ ceramic sample doped with 0.30 mol.% Dy₂O₃.

$$ {\text{Ti}}^{4 + } + e \to {\text{Ti}}^{3 + } $$

(11)

Figure 9a shows that two obvious peaks correspond to Ti 2p_1/2 and Ti 2p_3/2 of BE (binding energy) at 463.5 eV and 457.8 eV, which confirms the presence of Ti⁴⁺ ions.35 Furthermore, the other two weak peaks of BE at 458.2 eV and 457.5 eV are attributed to Ti³⁺.36 Figure 9b shows the O 1 s peaks for the TiO₂ sample. It can be seen that three peaks of BE exist at 530.8 eV, 529.5 eV and 529.0 eV. A major peak at 529.0 eV is related to the Ti-O bonds, and the other two peaks at 529.5 eV and 530.8 eV correspond to the existence of other cation-oxygen bonds (i.e., Nb-O, Dy-O and Si-O) and oxygen vacancies or surface hydroxyl, which verifies that some of the dopants (Nb, Dy, Si) enter the lattices and bond with oxygen.16,36 According to Eq. 7, the dopant of acceptor ions like Dy³⁺ can cause the formation of oxygen vacancies. The defects such as oxygen vacancies and free electrons can increase the conductivity of grains, thus improving the varistor properties of TiO₂ ceramics. Meanwhile, Fig. 9c shows two peaks in the BE spectrum of Nb at 209.1 eV as well as 206.3 eV, and the splitting of the spin–orbit is approximately 2.8 eV, which is consistent with the previous report, confirming the existence of Nb⁵⁺ ions.16 Figure 9d and e present only a single peak at 152.1 eV and 101.4 eV, respectively, verifying the presence of Dy³⁺ and Si⁴⁺.

Discussion

The dopant of Dy₂O₃ has a great influence on the microstructure and varistor properties of the Nb-Si co-doped TiO₂ ceramics. The model is shown in Fig. 10, where it can been seen that some Ti⁴⁺ ions in the lattice are replaced by Dy³⁺ ions after the addition of Dy₂O₃, which causes severe lattice distortion and some defect carriers such as oxygen vacancies are generated, thus making the grain more semiconducting.37,38 Therefore, the electrical properties are improved. At the same time, the remaining dopant (Dy₂O₃) segregates at grain boundary. A moderate content of Dy³⁺ segregating at the grain boundary improves depletion layer width and increases grain boundary barrier height. As a result, the nonlinear coefficient increases. Moreover, the moderate amount dopant of Dy₂O₃ also gives rise to the growth of grains. Notably, the secondary phase caused by trivalent ions is helpful to the decrease of dielectric loss.39 According to Eqs. 3 and 10 and the following Eq. 12, the breakdown voltage decreases, the nonlinear coefficient further increases and the dielectric constant ascends.

Fig. 10

The effects of the dopant Dy₂O₃ on the microstructure of Nb-Dy-Si co-doped TiO₂ ceramics.

$$ \varepsilon_{\text{r}} = \varepsilon_{\text{B}} D/t_{\text{B}} $$

(12)

where $\varepsilon_{\text{r}}$ is the dielectric constant, $\varepsilon_{\text{B}}$ is TiO₂ intrinsic dielectric constant, $D$ is the average grain size, $t_{\text{B}}$ is the mean width of the grain boundary.

However, excessive dopant of Dy₂O₃ will generate superfluous secondary phase, which inhibit grain growth and degrade the electrical properties. According to the previous report, the IBLC (internal barrier layer capacitance) effect is strengthened as the grain size diminishes.40 Therefore, a colossal dielectric constant can also be achieved in the TiO₂ samples containing a mass of secondary phases.40

Conclusion

By optimizing the sintering temperature and the doping content of Dy₂O₃, good comprehensive varistor properties were obtained in Nb-Dy-Si co-doped TiO₂ ceramic systems. The doping of Dy₂O₃ improves the varistor properties of TiO₂ ceramics. When the doping content of Dy₂O₃ was 0.30 mol.%, the TiO₂ ceramic system presented the best varistor properties, with a very low breakdown voltage (1.34 V/mm), good nonlinear coefficient (5.7) and colossal dielectric constant (8.01 × 10⁵) measured at 1 k Hz. Reassuringly, compared to the previous works,41,42 the TiO₂ ceramic system in this work has a higher dielectric constant, although the challenge of further reducing its dielectric loss still remains. Table V shows the comparison of electrical properties of different TiO₂ varistor samples. In conclusion, the comprehensive varistor properties of the TiO₂ ceramic system (99.80TiO₂-0.60Nb₂O₅-0.30Dy₂O₃-0.30SiO₂, mol.%) are better than the previous works, which makes it a potential candidate for low voltage varistors.8,12,14

Table V Comparison of electrical properties of different TiO₂ varistor samples