Abstract
The purpose of this work is to focus on the hydrodynamics of a Top-Submerged-Lance (TSL) smelting furnace, understanding how liquid properties and operational parameters act on key factors of a TSL process, such as splashing, mixing, mass transfer area, and bubble development. A deep knowledge of all those aspects is needed since they all influence the smelting reaction rates; hence the efficiency of the reactor. The characterization and scaling of the TSL gas injection are commonly based on the modified Froude number, the ratio of dynamic and gravitational forces. Detailed literature research reveals a potential weakness of this approach, since it does not consider the effects of viscosity and surface tension. To investigate this question an extensive parametric study was performed applying computational fluid dynamics to cold and non-reactive flows, which provided a broad overview of the physics of the flow. The analysis was performed on fluid dynamic properties (liquid density, liquid viscosity, surface tension) and operational variables (gas volume flow, lance immersion depth). The coupled Level Set—Volume of Fluid model, available in the commercial solver ANSYS Fluent®, was used to resolve the gas–liquid interface in the multiphase flow. The results of the work underscore the significance of the viscous and interfacial forces for gas injection in smelting slags, confirming the incompleteness of applying only the Froude number to describe such flows.
Similar content being viewed by others
Introduction
The Top-Submerged-Lance (TSL) technology today plays an active and significant role in the pyrometallurgical industry. Developed in the early 1970s to improve the tin smelting process, this technique rapidly reached commercialization, extending the field of application to other metals such as copper, lead, nickel, and zinc.[1] Eighteen percent of worldwide copper production employs TSL furnaces, as reported by Kapusta,[2] and recent investigations on metal recycling employ it to achieve sustainability in process metallurgy.[3] According to Reuter,[4] 64 commercial Ausmelt furnaces are being used to process Cu, Sn, Zn, Pb and Ni. Nevertheless, the young age of this process means that is still requires in-depth scientific research to improve its resource efficiency and reliability.
The main feature of these furnaces is the direct injection of process gas (air or O2-enriched air) through the top-submerged lance into the liquid slag bath at a temperature range of 1100 °C to 1400 °C: this creates a strong turbulent agitation in the bath, with the aim of increasing the gas–liquid interface and the mass transfer, and hence the overall reaction rates. The bubble rise and consequent break-up and splashing generate a recirculating structure in the liquid phase, which leads to a higher mass transfer in the liquid bath. The formation of stagnant zones is also prevented and, by that means, the localized solidification of slag. It therefore follows that knowledge of the hydrodynamic behavior of these furnaces is of crucial importance for a global comprehension of the entire process. It has to be noted that due to the high temperatures and the aggressive nature of the slags, in-situ measurements and optical inspections are still very challenging, meaning that many aspects of the underlying physics are currently not fully understood, and are handled with empirical approaches. The usage of Computational Fluid Dynamics (CFD) can help overcome these difficulties and answer many questions. However, the high complexity of this multiphase flow and the respective models (high temperature, reactive, and intrinsically transient) still restricts the applicability of this technique to small-to-pilot-scale reactors or to simplified test cases.
Indeed, various works have been done on down-scaled, cold, and non-reactive systems (mostly air–water), since direct access to the multiphase flow offers a better understanding and characterization of the injection. The scaling procedure used to obtain a lab-scale model from the full-scale reactor is hence a key factor in reproducing the nature of the injection: neglecting thermal and chemical similarities in the first instance, geometrical and dynamic similarities are usually applied. Morsi et al.[5] carried out an experimental campaign investigating the effect of a swirling flow at the lance inlet in an air–water system, varying the vertical position of the lance and the gas volume flow. The authors reported that a 150-tonne steel-making ladle was scaled to a one-sixteenth scale model, under conditions of dynamic and geometric similarity, in accordance with the work carried out by of Mazumdar and Guthrie.[6] They found out that the effect of the swirling jet is limited to the plume region, and that the lance immersion depth affects the flow more than the gas flow rate. Using the same scaled model, Mazumdar and Guthrie applied a numerical model in conjunction with experimental studies to predict gas injection in ladle metallurgy operations, such as desulfurization and decarburization of steel. They proposed a scale-up criterion based on the Froude number (see Eq. [1]), considering inertial and potential forces to dominate over viscous forces:
where \({\bar{U}}_{\text{r}}\) is the mean velocity of liquid recirculation, and H is the liquid depth. Similar considerations were suggested by Sahai and Guthrie,[7,8] who presented a hydrodynamic model for submerged gas injection in liquid stirring systems. The authors provided a relationship between the mean velocity of liquid recirculation \({\bar{U}}_{\text{r}}\) and the plume velocity \({U}_{\text{p}}\), whose expression was also derived. On the same topic, Mazumdar.[9] gave an overview of the dynamic similarity of gas-stirred ladle systems: again, he underlined that in gas-stirred ladles, flows are dominated by inertia and gravity, and the similarity question reduces to the usage of the Froude number. Also note that the kinematic viscosity of steel at the operating temperatures for ladle processes is comparable to that of water at room temperature. He advised against the application of the modified jet Froude number (see Eq. [2]) for ladle systems[10]
where \(U_{\text{g}}\) is the inlet velocity of the injected gas, and proposed the use of the plume velocity to define the Froude number, highlighting its unsuitableness for jetting regimes or in the presence of a top slag layer.
The same conclusion was reached by Krishnapisharody and Irons,[11] who reviewed the usage of the modified Froude number in ladle metallurgy in favor of a proposed model based on plume parameters. Critical remarks were directed at various aspects of the modified Froude number, such as the characteristic length used, or the importance of the initial momentum of the injected gas in comparison with buoyancy forces.
It should be noted that all of those works concern ladle metallurgy operations, where gas is injected at moderate regimes, in most cases from the bottom of the reactor and in hot liquid steel, which has different physical properties than those of the smelting slags. Despite that, these models have been applied in the literature for the hydrodynamic modeling of TSL smelting processes. Huda et al.[12] performed a CFD study of an Eulerian two-fluids model based on the work by Morsi et al. (see above) investigating the effect of swirling jetting on the nature of the flow, and proposed a semi-empirical equation to estimate the gas penetration depth as a function of the modified Froude number. Pan and Langberg[13] examined the behavior of large bubbles in bath smelting furnaces with 2D physical and numerical modeling, focusing on the mechanism of liquid splashing above the bath. The gas injection was scaled from a prototype Sirosmelt furnace under the condition of dynamic similarity of equal modified Froude number; they offered a qualitative overview of the splash generation, finding the liquid viscosity, the bubble size, and its detachment frequency as control parameters. A similar approach was used by Zhao et al.[14,15] for the experimental study of an air–water system: the authors analyzed the mixing process in the liquid phase using a saline solution as a tracer, and estimated the interface area of the main bubble formed at the lance.
Liovic et al.[16,17] implemented a Multi-Fluid Volume of Fluid (MFVOF) to resolve metallurgical flows, overcoming the difficulties of modeling multiphase systems with high density ratios: the shifted grid approach was used to compute density and the surface tension force was implemented with a fully kernel-based Continuum Surface Force (CSF) method. The model was tested on a scaled model of the Ausmelt furnace, but unfortunately no detailed information is given about the scaling procedure used. Their simulations were performed on air–water and air–glycerol systems to qualitatively understand the effect of viscosity on the multiphase flow field. A recent work was published by Wang et al.,[18] who investigated the usage of the appropriate turbulence model, using a Volume of Fluid approach. The results were compared with experimental data obtained from a setup with air injection in paraffin oil, using a vessel of 0.135 × 0.135 × 0.195 m. They found that the Renormalization Group \(k\epsilon \) model (RNG) and the Reynolds Stress Model (RSM) are able to predict time-averaged velocity fields. However, the Large Eddy Simulation (LES) model showed a better behavior in predicting fluctuating velocities and the Reynolds stress terms. Nevertheless, the usage of a LES-VOF approach could still be prohibitive to bigger lab-scale or even pilot-scale simulations, since a LES approach requires a considerably higher grid resolution than a RANS approach,[19] with consequent reduction of the time step to ensure that flow Courant number is less than 1. Some modeling activities have been carried out on pilot-furnace scales: Solnordal et al.[20] developed a mathematical model to calculate the heat transfer coefficient at the lance wall of a Sirosmelt prototype plant, as well as the thermal conductivity of the slag layer present over it. Huda et al.[21,22] provided a detailed analysis of the zinc slag fuming process in a TSL furnace, modeling the reactive slag bath as well as the coal combustion at the gas injector with an Eulerian multi-fluid approach.
The present study examines the importance of viscous and interfacial forces on the multiphase flow due to TSL gas injection. It is shown that the usage of only a modified Froude number is not sufficient when applied to injection into non-ferrous slag systems. To that end, an extensive parametric study has been done on the effect of physical properties (liquid density, viscosity, and surface tension) and operational parameters (vertical lance position, gas volume flow). The inclusion of these parameters is of considerable importance because, in addition to providing information about the hydrodynamic characterization, it can suggest some practical conclusions about how the control parameters affect important phenomena of the process, such as the mass transfer surface and the mixing of the liquid.
The Hydrodynamics of the TSL Injection in Smelting Furnaces
In this section, different aspects of the TSL process are discussed and the importance of hydrodynamics is highlighted.
Slag-Gas Interface Area
In TSL technology the interface between the slag and gas is a key element, since the smelting reactions take place there, unlike with a flash smelter, where the ores are oxidized in the so-called reaction shaft before reaching the settling region.[23]
There have been attempts to experimentally monitor this area in lab-scaled models,[14,15] despite obvious limitations. Zhao et al. monitored the flow with a high-speed camera and used image post-processing to calculate the contact area of the bubble at the lance in the instant of maximum penetration depth. The 2D view provides only a side projection of the interface; furthermore visibility is limited in the presence of an intense bubbling flow. The application of CFD coupled with multiphase interface-tracking methods such as Volume of Fluid (VOF), Level Set (LS), or Front-Tracking (FT) provides additional information and gives a deeper insight into the flow. In these methods, the spatial structure of all interfaces is known; hence the surface area can be readily computed, as well as its transient development.
Mixing Process in the Slag Phase
The downward gas injection into the slag bath generates a recirculating structure in the liquid flow, increasing heat and mass transfer.[24] As a consequence, the mixing process ensures high reaction rates and favors the transport of the matte from the reactive zone to the bath, where a gravity-driven settling process takes place. An unsuccessful stirring of the slag could cause the formation of solid agglomerates in regions where the recirculation is limited, which can lead to severe accidents such as explosions if they contain unburned fuel (coal, oil). Hence, an understanding of the mixing and recirculation is of importance for the process resource efficiency and selectivity, as well as for the process safety.
Slag Splashing
What makes a TSL furnace unique is the possibility to perform prompt manipulations of the mass transfer surface, which leads the smelting process. Besides the bubbles in the bath, the splashing of slag droplets represents a source of interface area. Its intensity and spread are critical design parameters. Properly designed, the splashing is beneficial to the productivity of the process and the lifetime of the furnace. However, if too intense splashing occurs, the spatters of slag constantly reach the refractory wall of the reactor, eroding it due to mechanical impact, thermal stress, and chemical degradation.[25] In the case of weak splashing, the gas-liquid interface and the mixing process inside the slag bath are reduced with direct consequences on the efficiency of the furnace. The optimal design should guarantee a range of splashed slag droplets comparable with the radius of the vessel, in order to prevent refractory deterioration and ensure mixing. The slag droplets also encounter the lance placed at the center of the chamber, on which they solidify, cooled by the inflowing process gas. The solid layer preserves the lance from the aggressive environment and from a direct contact with the slag. If the lance was not coated, the continuous alternation of gas and liquid slag could lead to disruptive phenomena such as thermal striping, a form of thermal fatigue damage. Well known in the design of nuclear reactors cooled with liquid metals (LMFR), it is caused by a random temperature fluctuation and a consequent thermal stress fluctuation because of the high thermal conductivities of the liquid, together with flow instabilities or the presence of a gas phase (as in the TSL reactor).[26]
Bubble Dynamics
The dynamics of the gas bubbles is of central relevance for the description of the TSL injection. Indeed it defines all the other aspects that have been discussed. The rise of the bubble towards the free surface induces a liquid displacement, which gives a poloidal direction to the streamlines inside the bath. This recirculating flow is what governs the slag mixing process.
Furthermore, the splashing phenomenon originates from the break-up of the bubbles once they reach the free surface, further increasing the interface area.
This can described in terms of bubble size and bubble detachment frequency, which are also closely connected.[13,15]
Rotational Sloshing Wave
It has been observed that gas injection into a liquid bath excites non-axisymmetric modes. In the presence of a cylindrical vessel, the waves generated from this instability begin to swirl around the central axis, generating the so-called rotational sloshing phenomenon.[27,28] When a heavy liquid, such as the slag-matte system, is agitated with a similar swirling motion, this can cause serious issues regarding the refractory nature of the wall and its mechanical structure.
Similarity Considerations
Given that the dynamic similarity drives the scaling criteria when investigating the hydrodynamics of the TSL gas injection, the fixed reference for all the considerations is the equation of momentum conservation (Eq. [3]), here expressed in the one-fluid formulation for a multiphase system with sharp interfaces, Newtonian fluids, and the condition of incompressibility:
The Navier–Stokes equation expresses a balance of forces acting on the infinitesimal control volume. Reformulating it in a dimensionless form yields:
where the first term is the Euler number, the ratio of pressure to inertial forces; the second term is the Reynolds number, the ratio of inertial to viscous forces; the third term is the Froude number, the ratio of inertial to gravitational forces; and the fourth term is the Weber number, the ratio of inertial forces to surface tension forces.
The choice of the Froude number, or its modified variants, as a meaningful dimensionless group for the description of the TSL injection indicates that the flow is inertia-gravity-driven. This assumption, derived for metallurgical ladle processes and extensively used in the literature, presents two main deficiencies when applied to non-ferrous smelting slags, namely regarding the viscous and the interfacial forces. The ratio of the viscosity of these slags to the viscosity of water has an order of magnitude of three (e.g.\(\mu _{{\text{slag}}, 1500 {\text{K}}}\) = 0.2 to 1 Pa/s, \(\mu _{{\text{water}}, 293 {\text{K}}}\) = 0.001 Pa/s,[29]) unlike in ladle metallurgy (e.g.\(\mu _{{\text{steel}}, 1900 {\text{K}}}\) = 0.007 Pa/s[30]), hence viscous forces might become significant. It should be also noted that the kinematic viscosity \(\mu/\rho \), which enters the Reynolds number, is comparable between water and liquid steel, and not between water and slag (e.g.\(\rho _{{\text{water}}, 293 {\text{K}}}\) = 1000 kg/m3, \(\rho _{{\text{steel}}, 1900 {\text{K}}}\) = 7000 kg/m3, \(\rho _{{\text{slag}}, 1500 {\text{K}}}\) = 3500 kg/m3[29,30]). Secondly, the TSL injection produces a main central bubble beneath the slag free surface, whose shape, and consequently dynamics, is determined by the surface tension acting at the interface (e.g.\(\sigma _{{\text{water}}, 293 {\text{K}}}\) = 0.074 N/m3, \(\sigma _{{\text{steel}}, 1900 {\text{K}}}\) = 1.5 to 1.8 N/m3, \(\sigma _{{\text{slag}}, 1500 {\text{K}}}\) = 0.4 to 0.5 N/m3[29,31]). The flow regime therefore differs from the ladle injection, where a bubbling plume region develops and where the Weber and Reynolds numbers can initially be left out from the analysis.
The presence of a gap in this topic is evident and challenging, because of the number of variables and hydrodynamic phenomena to examine.
Modeling Approach, Verification and Validation, and Data Analysis
The subject of this hydrodynamic study is gas injection through the lance into the bath. Other aspects of the process, such as the solid feed stream and the matte-slag interface, are not taken into account at the moment. In this section, the computational methods used in the CFD investigations are presented and explained in detail.
The CLSVOF Method
The modeling approaches used to describe a two-phase flow (gas, liquid) can be classified into two main categories: “multi-fluid” and “one-fluid” formulations.
In the multi-fluid model, also known as the Euler–Euler model, the phases interpenetrate in the domain and one set of Navier–Stokes equations is solved for each phase: to assure momentum and energy conservation, closure terms are needed for the interfacial friction and the heat transfer, since the interface is not resolved.
The second family includes the interface-tracking methods, which allow the numerical reconstruction of the material interface between the phases evolving in the system, therefore enabling the direct observation of the free surface and a deeper comprehension of the physics of the flow. The Volume of Fluid (VOF) and the Level Set (LS) models are the most common “one-fluid” models. A single set of Navier–Stokes equations is solved in the computational domain, which for a Newtonian, incompressible iso-thermal system of two fluids can be written as
where \(\vec {u}\) is the velocity vector, p is the pressure, \( \vec {f_{\text{g}}}\) is the gravitational force and \( \vec {f_\sigma }\) is the interfacial force due to the surface tension. In presence of a turbulent multiphase flow, as expected for a top-submerged gas injection, turbulence must be resolved or modeled. In a RANS (Reynolds-Averaged Navier–Stokes) modeling approach, further transport equations are added to the system. The k\(\epsilon\)-Realizable model, used in this work, considers two transport equations for the turbulent kinetic energy k and its rate of dissipation \(\epsilon \):
where
\(G_{\text{k}}\) is the generation of turbulent kinetic energy due to the mean velocity gradients, \(G_{\text{b}}\) is the generation of turbulent kinetic energy due to buoyancy, \(\sigma _k\) and \(\sigma _\epsilon \) are the turbulent Prandtl numbers, \(C_1\), \(C_2\) and \(C_3\) are constants. The fluid properties \(\rho (\alpha )\) and \(\mu (\alpha )\) are defined as follows
where \(\alpha \) is the volume fraction, \(\rho _{\text{l}}\) is the density of the liquid phase, \(\rho _{\text{g}}\) is the density of the gas phase, \(\mu _{\text{l}}\) is the dynamic viscosity of the liquid phase and \(\mu _{\text{g}}\) is the dynamic viscosity of the gas phase.
In the VOF model, the volume fraction \(\alpha \) is a discrete function, defined by
which jumps from 0 to 1 at the interface. This function is advected in the given velocity field, according to the advection equation in the conservative form
In the LS model, the advection equation is solved for a smooth marker function \(\phi \) defined by
The volume fraction is calculated and represented with the Heaviside function \(H_\delta (\phi )\), used to average the fluid properties (density and viscosity)
where \(\delta \) is the thickness of the interface.[32,33]
The Coupled Level Set—Volume of Fluid (CLSVOF) model merges the two approaches to capitalize on their strengths, by solving the VOF advection algorithm and additionally computing the LS equation. Because of the direct advection of the volume fraction in the VOF algorithm, the mass conservation is preserved, which is a main issue of the LS approach. On the other hand, the implementation of the surface tension force is a potential weakness of the VOF model, especially when applied to high density and surface tension ratios,[34,35] as for modeling smelting slags and mattes. According to the continuum surface force (CSF) model proposed by Brackbill et al.,[36] the surface tension is included as a volumetric source term in the momentum equation, and the discontinuity of the volume fraction does not allow the direct calculation of the normal vector and the curvature of the interface. The imbalance of forces at the interface leads to pressure fluctuations and consequently to the formation of the so-called “spurious currents”, which are unphysical phenomena and can even cause the break-up of the interface.[37]
To overcome this problem, the continuous level set function \(\phi \) is used to calculate the normal vector and the curvature of the interface, for which ordinary discretization schemes can be applied:
where \(\vec {n}\) is the normal vector of the interface, and \(\kappa \) is the curvature of the interface. It has to be noted that the addition of one equation implies an increase in the computational time, which may represent a limiting factor when dealing with a 3D approach and on a large-scale reactor.
The CLSVOF model is available in the commercial software ANSYS Fluent®, used for the research activity presented in this article.
Model Verification and Validation
The model is first verified and validated to show its reliability for the subsequent parametric study in the TSL furnace geometry.
Verification assessment
The verification of a model should demonstrate the correct implementation of the theoretical concepts. Therefore, reference cases for this step should be analytical solutions, or benchmark numerical solutions to ODEs or PDEs. Unfortunately, it is almost impossible to have analytical solutions of interfacial flows with complex topological transitions.
A numerical benchmark proposed by Hysing et al.[38] is chosen here as reference to verify and compare the CLSVOF and VOF models available in ANSYS Fluent®. A two-dimensional bubble of fluid B rises in fluid A from an initial state of quiescence; Figure 1 shows the geometry and the initial condition of the test case. Two different flow configurations were analyzed, varying the physical properties of fluids A and B, as summarized in Table I.
As the first step of this assessment, an analysis of grid convergence was performed on three different cells sizes h (1 / 100, 1 / 200, 1 / 400 mm). A deviation of 7.5 pct was observed for the bubble rise velocity between Grid 1 and Grid 3, and 1.6 pct for the bubble’ s center of mass. Consequently, the finer grid was used for the following evaluations (Figure 2).
The results of this study are presented in terms of the rising velocity and position of the center of mass of the bubble, for test case 1 (Figure 3) and for test case 2 (Figure 4). The CLSVOF model is compared to the VOF model and to the results obtained by Hysing et al., who used a LS method implemented in a Finite-Element code (TP2D). A good agreement between CLSVOF and VOF is observed, as well as with the reference data.
The shape of the bubble after a time of 3s is compared in Figure 5, for both flow configurations. Here, too the shape of the bubbles obtained with the different methods agrees qualitatively well with the reference case. Only the vertical position is slightly underestimated. As expected, the results of the CLSVOF model are closer to the reference, since a LS method was applied there. Furthermore, the break-up phenomenon appearing in test case 2 seems to be captured more effectively than in the VOF model, whose results show the formation of unphysical sharp trailing strands.
Validation assessment
A validation study should prove the capability of a model to represent a real physical phenomenon and determine its reliability as an engineering tool. The numerical results must be compared to experimental data, directly obtained from the system under investigation or from a simplified test rig.
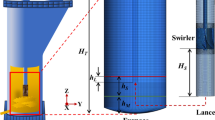
The experimental campaign carried out by Morsi et al.[5] carried out at CSIRO is taken as a reference to validate the CLSVOF model for the simulation of a Top-Submerged-Lance gas injection into a liquid bath. As reported in the first chapter, a one-sixteenth-scale air–water model (Figure 6) was used to investigate the effect of the swirl gas injection on the multiphase flow. The air (\({\dot{Q}} = 2.67\times 10^{-3}\)\({\text{m}}^{3}/{\text{s}}\)) flows through the lance into the water bath, encountering a helical element with a swirling angle of 57.5 deg. The velocity field was measured with a 2D Laser Doppler Anemometer (LDA) on 9 \(\mu \)m seeding particles, the results are available on a vertical plane passing through the center line of the cylindrical vessel, in the form of time-averaged profiles and contour plots.
The CFD simulation, performed with ANSYS Fluent®, employs a 2D axi-symmetric swirl solver and the CLSVOF method as a multiphase model. The turbulence is modeled with a RANS approach, namely with the k\(\epsilon\)-Realizable model. The SIMPLE algorithm is used for the pressure-velocity coupling, while second-order upwind schemes are employed for the spatial discretization of momentum and velocity and first-order upwind schemes for turbulence and the Level Set function. Finally, the Geo-Reconstruct scheme is applied for the volume fraction. The time step is set to 1 × 10−5 s, to ensure that the Courant number is smaller than 0.5. The spatial convergence was examined with a grid convergence study on four refinement levels, summarized in Table II. The grid independence is accomplished with a cell size of 1 mm (Grid 3), as seen from the results in Figure 7, which reports the air pressure drop and the time-averaged swirl velocity profile for the phase water at a height of 45 mm. Around 65 pct of deviation is observed for the peak of the \(\langle v_{w,\theta }\rangle \) distribution between Grid 3 and Grid 1.
The CFD results are compared with the experimental data (Figures 8 and 9) in terms of water velocity contour plot and profiles, evaluated at a height of 45 mm, right below the lance tip. Since just one velocity field is solved in the CLSVOF, a post-processing step is needed to compute the time-averaged velocity of the phase water:
Reasonable agreements are observed between the experimental data and simulation results, and the main features of the flow are captured well, except for an underestimation of the air-induced swirling motion in the water (Figure 10). One reason for the discrepancy could be related to the usage of the 2D axi-symmetric approach, which assumes zero gradients in the circumferential direction. However, the largest deviations are mainly seen in the region of injection with high void fractions, above 70 pct as shown in Figure 11. The reliability of LDA techniques used for the measurements in Reference 5 is therefore highly limited in this area. Kumar et al.[39] restrict the applicability of LDA to void fractions less than 15 to 20 pct.
Parametric Study
An extensive study on the influence of different liquid properties (\(\rho \), \(\mu \), \(\sigma \) of the liquid phase) and operating conditions (gas flow rate, lance immersion rate) is carried out to study its impact on the TSL hydrodynamics. The goal of the investigation is to provide a better understanding of the relationship between the physical parameters and the multiphase flow, as a first step towards the identification of an appropriate hydrodynamic scaling procedure for TSL furnaces. The range of parameters used in the study are given in Table III. The physical properties of the liquid are varied in the range from close to water up to typical values for a smelting slag. The gas flow rate and the lance position are varied in a broad range of possible operating conditions.
The simulations are performed on a geometrical model similar to the one used in the validation assessment (Figure 6), except for the presence of the swirler in the gas injection pipe. Indeed, the main objective of the investigation is to understand the dynamics of the multiphase system, specifically the interaction between kinematic, gravitational, viscous, and surface forces acting on the gas bubbles; hence the effect of swirl or non-swirl gas injection is not discussed. The inlet is placed directly at the tip of the lance, the outlet on the top of the vessel and all the other surfaces are set to no-slip wall condition. The numerical setup is again summarized for clarification:
-
2D axi-symmetric approach
-
CLSVOF method
-
\(k\epsilon \)-Realizable RANS model
-
SIMPLE scheme for \(p-u\) coupling
-
Second-Order Upwind: momentum, velocity
-
First-Order Upwind: turbulence, Level Set function
-
Grid size: 0.001 m (independence proved)
-
Time size: 1 × 10−5 s (Courant number < 0.5)
The choice of the 2D axi-symmetric approach derives from an analysis of computational efforts. All the simulations were performed on 48 CPUs, allocated at the HPC Cluster of the Center for Information Services and High Performance Computing (ZIH) at TU Dresden. The authors are aware that a multiphase flow has a 3D, asymmetric nature. However, bearing in mind that the purpose of a parametric study is to evaluate trends and that the 3D time-averaged solution is axi-symmetric (Figure 12), the above-mentioned solution is adopted and the order of computing days and CPUs is reduced from O(100) to O(10).
Several aspects of the multiphase flow are observed during the simulation and compared between the different configurations.
Gas–liquid contact area
The time-dependent contact area between the gas and liquid is directly extracted from the CFD simulation, monitoring the iso-surface computed at \(\alpha \) = 0.5. A time-averaged value, on a time range of 20 seconds, is then calculated. The first 4 seconds are skipped for averaging, to avoid initialization effects.
Liquid splashing
The time-averaged distribution of the liquid volume fraction is used to quantify the splashing of the liquid phase above the bath level. In fact, it represents the probability distribution of the presence of liquid in the time of observation: if one cell of the domain has a time-averaged liquid volume fraction of 1, the probability that the liquid is in that cell for the elapsed time is equal to 100 pct. As shown in Figure 13, the distribution is filtered firstly in space, focusing just on the region above the free surface, and secondly excluding the value 0 from the distribution, as regions with a 100 pct probability of gas presence are not useful for the evaluation of the splashing areas. A value of 0.5 pct is used as a lower threshold. A region is thus selected that has a probability between 0.5 and 100 pct of liquid being found in the gas domain in a temporal window of 20 seconds: this domain is defined as the Splashing Domain (SD [\({\text{m}}^3\)]) and it is used to compare the various configurations.
Global mixing time
The mixing time is evaluated using the concept of mixing uniformity. A tracer, with the same properties as the evolving liquid, is injected into the domain from the lance tip and transported into the bath via convection. The mixing time \(T_{95}\) is defined as the time at which the 95 pct of uniformity is reached, according to the uniformity index defined in Eq. [22]:
where \(Y_{\max }\), \(Y_{\min }\) are the maximum and minimum mass fraction of the tracer in the liquid, respectively, and \(Y_\infty \) is the tracer mass fraction at 100 pct uniformity. Two other indexes were tested, namely
even though the \(U_\Delta \) better represented the uniformity, including local and global information on the mixing. This function is calculated over the entire liquid domain, so that the information about the mixing time guarantees more accuracy than the tracking with local probes. A snapshot of the spatial distribution of the tracer together with the corresponding temporal evolution of the uniformity index up to that specific point of time is shown in Figure 14.
Bubble size at detachment
The size of the bubbles is evaluated on their detachment from the lance, namely in the first moment that the bubble is disconnected from the injection tip. This is visually determined from the volume fraction distribution: each 0.01 seconds analogous pictures are extracted from the CFD software, and an image post-processing approach is used to identify the gas bubble and calculate its size, as shown in Figure 15. Information about the shape of the bubbles at detachment is quantified using the concept of sphericity, as in Eq. [25]:
where \(A_{{\text{bubble}}}\) is the surface area of the bubble and \(A_{{\text{eq, sphere}}}\) is the surface area of an equivalent sphere with the same volume. As for the other phenomena, the results are averaged over a time range of 20 seconds.
Results
The next paragraphs present the results of the parametric study. For each independent variable, the effects on the observed phenomena previously described are quantified and presented in percentages relative to the baseline configuration. To help the reader, the base configuration is reported with a white dot in the plots.
Operational Parameters
The vertical shift of the lance and the amount of gas injected into the bath are the principal control parameters of a TSL furnace. Therefore, it is extremely valuable to have a deeper understanding of their action on phenomena such as mixing or mass transfer at the gas-liquid interface. They have a direct influence on the hydrodynamics of the flow; hence they must be taken into account when a scaling approach is applied to these reactors.
Lance immersion depth
The control of the immersion depth of the lance inside the liquid slag is crucial, specifically in running a batch process, where the height of the bath varies with time. Figure 16 shows the impact of this variable on the main characteristics of the flow. The surface of the main bubble at the tip of the lance increases almost linearly with the immersion of the lance, together with a decrease in sphericity. As supported by Figure 17, in the deepest lance position the bubbles are larger and present a more elongated and indented shape. The overall gas-liquid contact area is almost tripled from the first to the last lance position. However, the slope is higher for lower immersion depths and levels off for deeper immersions, probably because of the plateau reached by the splashing at \(H_{\text{L}} = 0.1\) m. The splashed droplets indeed, together with the bubbles in the bath, define the interface area. A deeper immersion of the lance generates a more agitated turbulent flow in the bath, with larger bubbles and higher gas entrainment, also favoring the mixing of the liquid. At \(H_{\text{L}} = 0.025\) m, the mixing is more than three times slower compared with the base configuration with \(H_{\text{L}} = 0.1\) m.
Gas flow
The amount of process gas injected into the bath directly affects to the overall reaction rate of the process, since it is a reactant of the system. A further indirect contribution is its effect on the hydrodynamics. As shown in Figure 18, one can see that the total interface area increases linearly with the volume flow. When the gas flow rate is increased by a factor of 3, the contact area increases by a factor of about 2. This increment can be partly explained by the increasing bubble size and consequently the stronger splashing, as reported in Figure 19. It is interesting to note that the shape of the bubble does not change significantly between the configuration at the smallest and highest flow rate, as confirmed by its almost constant sphericity. As observed for the immersion depth, the stronger agitation of the bath leads to faster mixing in the liquid. The Global Mixing Time is halved from \({\dot{Q}}_1\) to \({\dot{Q}}_5\).
Fluid Properties
The parametric analysis of the fluid properties \(\rho \), \(\mu \) and \(\sigma \), ranging from water to slag values, is intended to understand the importance of gravitational, viscous, and interfacial forces in the hydrodynamics of the TSL gas injection.
Liquid viscosity
The viscosity of the liquid bath can even be considered as a control parameter of a furnace, since it can significantly vary during an operation campaign, with varying temperature and composition. It can also lead to undesired phenomena such as the foaming of the slag, which increases with increasing viscosity.[40] Figure 20 shows the results of the parametric study. One can see that the viscosity significantly affects the contact area between the gas and the liquid phase, as expected. Figure 21 shows snapshots of the simulations for the lowest value of \(\mu _1\)=0.001 Pa/s and for the highest value of \(\mu _4\)=1 Pa/s. The larger interface area at the highest viscosity is explained with the formation of numerous smaller bubbles, which are deeply entrained in the bath. In this configuration, the interface is therefore established in the bubble-liquid contact area. Indeed, the droplet-gas area represented by the splashing is considerably reduced at \(\mu _4\). Namely, the splashing domain is reduced by 80 pct from \(\mu _1\) to \(\mu _4\).
Concerning the Global Mixing Time, a curious behavior is encountered: an increase in mixing time by around 400 pct is observed when the dynamic viscosity is increased from 0.001 to 0.1 Pa/s, and then it steeply drops all the way back to a value of about − 30 pct for a viscosity of 1 Pa/s. Since the tracer is transported exclusively via convection, the explanation must lie on the recirculation structures of the liquid bath, which are induced by the rise of the bubbles around the lance. Figure 22 depicts the time-averaged cells of recirculation for the four cases, with the visualization of streamlines for the liquid phase. It is evident that, in the fourth configuration, the eye of the recirculating structure has an elongated shape and is positioned lower, compared with the first three viscosities, probably because of the high gas entrainment. The dead zone in the lower corner of the domain is also much smaller. Hence there is a better distribution of the tracer throughout the domain for the highest viscosity, whereas for the lower viscosities the global mixing time is governed by the slow process of the tracer being transported into the lower corner of the domain. This change in the recirculating flow is also confirmed by a change in the shape and motion of the main bubble, as observed in the plots of bubble surface and sphericity. The trend of decreasing surface and increasing sphericity is interrupted at \(\mu _4\).
Liquid density
In Figure 23 the parametric analysis on \(\rho \) is presented. Apart from the gas-liquid interface, increased by around 40 pct from \(\rho =1000\) kg/m\(^3\) to \(\rho =4000\) kg/m\(^3\), no clear trends are observed for the other phenomena, where the range of variability is somewhat restricted if compared with the other parameters.
Surface tension
Figure 24 shows that moving from \(\sigma _1\) to \(\sigma _4\) the interphase area is reduced by almost 35 pct: in a multiphase system with high surface tension, the structures of the dispersed phase, whether bubbles or droplets, tend to minimize the contact area with the continuous phase. Similarly, with an increase in the surface tension by a factor of about 5, the splashing domain is approximately halved in size. It is interesting to note that changing the surface tension and dynamic viscosity leads to a similar change in size of the splashing domain, whereas opposite changes are observed for the interfacial area. Flows with high surface tensions result with faster mixing. When the surface tension is increased by a factor of 3, the mixing time is reduced to 50 pct, than reaches a plateau. As already noted for the overall gas-liquid contact area, the surface tension acts to minimize the surface of the bubbles. Indeed, Figure 24 indicates that at high surface tension the bubbles detach with a more spherical shape. Note, however, that the change in the bubble surface is small, only about 15 pct when the surface tension changes from \(\sigma _1\) to \(\sigma _4\).
Summary and Conclusions
The Coupled Level Set—Volume of Fluid model was applied to investigate the hydrodynamics of gas injection with a Top-Submerged-Lance in a liquid bath. A parametric study on liquid properties and operational parameters was carried out to assess the response of the multiphase system and to show the importance of the viscous and interfacial forces involved; hence to gain knowledge for its hydrodynamic characterization. Various phenomena of the multiphase flow were monitored, such as the gas-liquid interphase, liquid splashing, the mixing process in the bath, and the detachment of the bubbles. All these aspects of the flow must be considered to entirely describe the hydrodynamics of a TSL smelter since they all strongly influence the mass and heat transfer in the process, and by that the reaction rates. The results presented in Sections IV–A–1 through IV–A–3 show a strong effect of the liquid viscosity and the surface tension on the nature of the flow. As a consequence, the usage of the Froude number as a unique dimensionless group can not be sufficient to characterize the multiphase flow and scale down a TSL smelting furnace, since viscous and interfacial forces are not taken into account. It was furthermore observed that an increase in viscosity and surface tension does not produce a consistent response when different phenomena are studied: i.e., if the splashing of the liquid is reduced by higher \(\mu \) and \(\sigma \), on the other hand the interphase area escalates with \(\mu \) and diminishes with \(\sigma \). This indicates that a scaling approach applied to scale down phenomenon A may not be appropriate to scale down phenomenon B, even taking into account viscous and interfacial forces. More effort should be made in the development of a thorough dimensional analysis of the TSL hydrodynamics, together with the exploration of new fluids which are easy to handle in labs and whose properties are closer to the smelting slags.
Change history
10 October 2019
The article The Importance of Viscous and Interfacial Forces in the Hydrodynamics of the Top-Submerged-Lance Furnace, written by Obiso <Emphasis Type="Italic">et al</Emphasis>. was originally published electronically on the publisher’s internet portal on July 3, 2019 without open access. With the author(s)’ decision to opt for Open Choice the copyright of the article changed on October 3, 2019 to © The Author(s) 2019 and the article is forthwith distributed under a Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
References
J. M. Floyd: Metall. Trans. B, 2005, vol. 36, pp. 557–575.
J. Kapusta: in EXTRACTION 2018 Conf., 2018.
M. A. Reuter: Metall. Trans. B, 2016, vol. 47(6), pp. 3194–3220.
M.A. Reuter: in GDMB Lead Meeting, 2014.
Y. Morsi, W. Yang, B. Clayton , N. Gray: Can. Metall. Q., vol. 39(1), pp. 87–98. (2000)
D. Mazumdar , R. I. L. Guthrie: Metall. Trans. B, 1985, vol. 16(1), pp. 83–90.
Y. Sahai and R.I.L. Guthrie: Metall. Trans. B, 1982, vol. 13(2), pp. 193–202.
Y. Sahai and R.I.L. Guthrie: Metall. Trans. B, 1982, vol. 13(2), pp. 203–11.
D. Mazumdar: Metall. Trans. B, 1990, vol. 21(5), pp. 925–928.
N. B. Ballal , A. Ghosh: Metall. Trans. B, 1981, vol. 12(3), pp. 525–534.
K. Krishnapisharody , G. A. Irons: Metall. Trans. B, 2013, vol. 44(6), pp. 1486–1498.
N. Huda, J. Naser, G. Brooks, M. A. Reuter , R. W. Matusewicz: Metall. Trans. B, 2010, vol. 41(1), pp. 35–50.
Y. Pan, D. Langberg: J. Comput. Multiphas. Flows, vol. 2(3), pp. 151–164. (2010)
L.-F. Zhang, H.-L. Zhao, P. Yin, and S. Wang: Int. J. Miner. Metall. Mater., 2016, vol. 23(12), pp. 1369–76.
H. Zhao, L. Zhang, P. Yin, and S. Wang: Int. J. Chem. React. Eng., 2017, https://doi.org/10.1515/ijcre-2016-0139.
P. Liovic, J.-L. Liow, M. Rudman: ISIJ Int., 2001, vol. 41(3), pp. 225–233.
P. Liovic, M. Rudman , J. L. Liow: Appl. Math. Model., 2002, vol. 26(2), pp. 113–140.
Y. Wang, M. Vanierschot, L. Cao, Z. Cheng, B. Blanpain , M. Guo: Chem. Eng. Sci., 2018, vol. 192, pp. 1091–1104.
R. Schwarze: CFD-Modellierung, Springer, Berlin, Heidelberg, DE, 2013, pp. 129–180.
C. B. Solnordal, F. R. A. Jorgensen , R. N. Taylor: Metall. Trans. B, 1998, vol. 29(2), pp. 485–492.
N. Huda, J. Naser, G. Brooks, M. A. Reuter , R. W. Matusewicz: Metall. Trans. B, 2012, vol. 43(1), pp. 39–55.
N. Huda, J. Naser, G. A. Brooks, M. A. Reuter , R. W. Matusewicz: Metall. Trans. B, 2012, vol. 43(5), pp. 1054–1068.
M. Schlesinger, M. King, K. Sole , W. Davenport: Extractive Metallurgy of Copper, 5th ed., Elsevier, Oxford, UK, 2002, pp. 155–175.
E. N. Mounsey , K. R. Robilliard: JOM, 1994, vol. 46(8), pp. 58–60.
H. Y. Sohn, A. Malfliet, L. Scheunis, P. T. Jones , B. Blanpain: Treatise on Process Metallurgy, 1st ed., Elsevier, Oxford, UK, 2014, pp. 534–624.
K. Velusamy, K. Natesan, P. Selvaraj, P. Chellapandi, S. C. Chetal, T. Sundararajan , S. Suyambazhahan: CFD4NRS, 2006.
M.P. Schwarz: Chem. Eng. Sci., 1990, vol. 45(7), pp. 1765–1777.
M. Iguchi, T. Uemura, H. Yamaguchi, T. Kuranga , Z. Morita: ISIJ Int., 1994, vol. 34(12), pp. 973–979.
P. J. Mackey: Can. Metall. Q., 1982, vol. 21(3), pp. 221–260.
S. Ghorai, G. G. Roy, S. K. Roy: Ironmaking Steelmaking, 2004, vol. 31(5), pp. 401–408.
P. Sulasalmi, V. V. Visuri, A. Kärnä and T. Fabritius: Steel Res. Int., 2015, vol. 86(3), pp. 212–222.
G. Tryggvason, R. Scardovelli , S. Zaleski: Direct Numerical Simulations of Gas-Liquid Multiphase Flows, 1st ed., Cambridge University Press, Cambridge, UK, 2011, pp. 75–132.
ANSYS ® Fluent, 17.2, Help System, ANSYS Fluent Theory Guide, ANSYS, Inc.
D. Gerlach, G. Tomar, G. Biswas , F. Durst: Int. J. Heat Mass Transfer, 2006, vol. 49(3-4), pp. 740–754.
S. Popinet, S. Zaleski: J. Comput. Multiphase Flows, 2017, vol. 30(6), pp. 775–793.
J. U. Brackbill, D. B. Kothe , C. Zemach: J. Comput. Phys., 1992, vol. 100(2), pp. 335–354.
B. Lafaurie, C. Nardone, R. Scardovelli, S. Zaleski , G. Zanetti: J. Comput. Phys., 1994, vol. 113(1), pp. 134–147.
S. Hysing, S. Turek, D. Kuzmin, E. Burman, S. Ganesan , L. Tobiska: Int. J. Numer. Methods Fluids, 2009, vol. 60, pp. 1259–1288.
S. Kumar, M. Duduković , B. Toseland: Non-Invasive Monitoring of Multiphase Flows, 1st ed., Elsevier Science B.V., Amsterdam, NED, 1997, pp. 1–45.
K. Ito , R. J. Fruehan: Metall. Trans. B, 1989, vol. 20B(4), pp. 509–514.
Acknowledgments
The authors would like to thank the Center for Information Services and High Performance Computing (ZIH) at TU Dresden for the allocation of the computing time. The German Federal Ministry of Education and Research (BMBF) has funded this research within the framework of the Center for Innovation Competence Virtuhcon (Project Number 03Z22FN11). The author is responsible for the content of the publication.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Manuscript submitted December 4, 2018.
The original version of this article was revised due to a retrospective Open Access order.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Obiso, D., Kriebitzsch, S., Reuter, M. et al. The Importance of Viscous and Interfacial Forces in the Hydrodynamics of the Top-Submerged-Lance Furnace. Metall Mater Trans B 50, 2403–2420 (2019). https://doi.org/10.1007/s11663-019-01630-z
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11663-019-01630-z