Introduction

Porous metals, or metallic foams, are metals with pores deliberately integrated in their structure.[1] The pores are of crucial importance because they give new properties to the material. For applications requiring good permeability to fluids, the internal network of the cells in the porous metal must be open. The open-cell porous metals are emerging as an effective material for heat transfer management.[2]

In active cooling applications using the open-cell structures, the cooling system is composed of the porous metal medium and the fluid is used as a coolant flowing through the material. In the design of heat exchangers with porous metals, two key properties are important: the heat transfer coefficient and the pressure drop across the sample,[3] which are strongly affected by the pore structure.[4]

Porous copper manufactured by the space holder methods, such as the Lost Carbonate Sintering (LCS) process,[5] is a promising type of material for use as heat exchangers.[6] However, there is a very limited amount of data available on the fluid flow and the heat transfer behavior of this type of materials. Measurements of fluid permeability and heat transfer coefficient are difficult and time-consuming.

Numerical simulation has gained popularity as a reliable tool to study heat transfer in porous media. For example, Teruel and Rizwan-Uddin[7] numerically calculated the interfacial heat transfer coefficient in porous media. Xin et al.[8] numerically investigated the heat and mass transfer behaviors in porous media for multiphase flow. Hwang and Yang[9] simulated the heat transfer and fluid flow characteristics in a metallic porous block subjected to a confined turbulent slot jet. Numerical simulation has shown to be a very useful and consistent tool.

Different approaches have been considered in tackling the porous media problem. One methodology is considering the porous media as an arrangement of tube banks in 2D.[10] Another practice is creating a representative 3D cell structure.[11] A different technique is creating a random walled structure acting as the porous matrix.[12]

This paper studies the fluid flow and heat transfer in open-cell porous metals by numerical simulation using ANSYS Fluent. A 3D representative elementary volume (REV) has been created to represent the porous structure of LCS porous copper, allowing for different combinations of porosity, pore size, and metal particle size.

Numerical Simulation

Representative Elementary Volume (REV)

The REV used to represent the porous structure of LCS porous copper in this study is composed of 5 FCC unit cells similar to the one shown in Figure 1. To create the unit cell, the spherical pores are arranged in the same way as that the atoms are arranged in the FCC structure. The pores are connected by cylindrical open channels at the contact points. The porosity of the REV is varied by changing the radius of the cylinder, r c, and the distance between the centers of the neighboring spheres, l s.

Fig. 1
figure 1

FCC unit cell to represent the porous structure

Full size image

The radius of the cylinder is selected to reflect the size of the necks or windows connecting the neighboring pores in the LCS porous copper, which is determined by the sizes of the \( {\text{K}}_{2} {\text{CO}}_{3} \) and \( {\text{Cu}} \) particles and can be calculated by Eq. [1].[13,14]

$$ A_{\text{sc}} = \frac{\pi }{2}\left( {d_{{{\text{K}}_{2} {\text{CO}}_{3} }} } \right)^{2} \left( {1 - \frac{{\left( {\varphi + 2} \right)}}{{\sqrt {\varphi^{2} + 6\varphi + 5} }}} \right), $$
(1)

where \( A_{\text{sc}} \) is the area of the neck, \( d_{{{\text{K}}_{2} {\text{CO}}_{3} }} \) is the K2CO3 particle diameter, and \( \varphi \) is the K2CO3-to-Cu particle size ratio, i.e., the ratio between the diameters of the K2CO3 and Cu particles.

The coordination number, or the number of contacts of a sphere with its neighbors, is 12 in the FCC structure. In LCS porous metals, however, the coordination number, ω, is much lower and can be estimated by Eq. [2].[13]

$$ \omega = \frac{2}{{\left( {1 - \frac{{\left( {\varphi + 2} \right)}}{{\sqrt {\varphi^{2} + 6\varphi + 5} }}} \right)\left( {1 - \varphi + \frac{\varphi }{\varepsilon }} \right)}}, $$
(2)

where ε is the porosity.

To account for this difference, the total area of the necks in the REV is considered to be equal to the total area of the necks of a pore in the real porous material. The radius of the cylinders used in the REV can therefore be obtained by Eq. [3].

$$ r_{c} = \sqrt {\frac{{\omega \cdot A_{sc} }}{12\pi }} $$
(3)

Given the pore size, \( d_{{{\text{K}}_{2} {\text{CO}}_{3} }} \), the cylinder radius, r c, and the porosity, ε, the distance between the centers of the neighboring spheres, l s, can be determined.

The values of the cylinder radius and the distance between the centers of the neighboring spheres for each combination of pore size and porosity are presented in Table I. In this study, the \( {\text{Cu}} \) particle size is fixed as 50 μm.

Table I Cylinder Radius and Distance Between Neighboring Spheres for the FCC Unit Cells
Full size table

Governing Equations and Boundary Conditions

Incompressible Newtonian flows at pore-scale level are governed by the Navier–Stokes equations. For this study, the \( k - \varepsilon \) model was used. The continuity, momentum, and energy equation are given by Eqs. [4] through [6].

$$ \rho \nabla v = 0 $$
(4)
$$ \left( {v \cdot \nabla } \right)v = \nabla \cdot \left[ { - PI + \mu \left( {\nabla v + \left( {\nabla v} \right)^{T} } \right)} \right] $$
(5)
$$ \rho C_{p} v \cdot \nabla T = \nabla \cdot \left( {k\nabla T} \right), $$
(6)

where \( \rho \) is the density of the fluid, \( v \) is the velocity, P is pressure, I is the identity matrix, \( \mu \)is the viscosity of the fluid, \( T \) is the temperature, \( C_{p} \) is the specific heat, and \( k \) is the thermal conductivity.

Simulations were carried out using ANSYS Fluent CFD with different REVs to account for different combinations of pore size and porosity as shown in Table I. The parameters considered for this analysis were pore size, porosity, and volumetric flow rate.

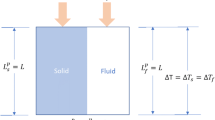
The computational domain is composed of three parts: a fluid channel long enough for the fluid to be fully developed, the REV in the fluid channel that represents the porous metal, and a solid copper block underneath the REV supplying a constant heat flux (Figure 2). The working fluid used in this study is water.

Fig. 2
figure 2

Representative Elementary Volume (REV) and computational domain

Full size image

A constant heat flux (J = 250 kW/m2) was set at the bottom of the solid block. The heat is transferred from the block to the REV via conduction and is removed from the REV by forced convection using water. The top of the domain was set as zero heat flux. The other two sides of the domain were set as symmetric. The initial temperature for the whole domain was set as 300 K (27 °C).

The velocity, pressure, and temperature fields in the fluid phase of the domain were investigated. The governing equations were solved numerically and numerical computations were performed for a wide range of porosity (50 to 80 pct), pore size 400 to 1000 µm, and Darcian flow velocity (0.02 to 0.3 m/s) or flow rate (0.2 to 1.8 l/min). A total of 120 simulations were carried out in order to analyze and compare the effects of these parameters.

In this study, the overall quality of the mesh was >0.9 in all cases. The numerical computations were considered to be converged when the residuals of the variables were lowered by six orders of magnitude (i.e., \( \le 10^{ - 6} \)). Double precision conditions were selected at solver to minimize the possibility of errors.

Permeability and Form Drag Coefficient

According to Darcy’s law for unidirectional flow through a porous medium in creeping flow regime, the pressure drop per unit length is proportional to the superficial fluid velocity as shown in Eq. [7].

$$ \frac{\Delta P}{\Delta L} = \frac{\mu }{K}u, $$
(7)

where \( \Delta P \) is the pressure drop between the inlet and outlet of the porous media, \( \Delta L \) is the length of the porous media, \( \mu \) is the viscosity of the fluid, \( u \) is the Darcian velocity of the fluid (i.e., flow rate divided by the cross-sectional area), and \( K \) is the permeability of the porous media.

If the Reynolds number, Re, increases to a critical value, the fluid will become turbulent and this relationship will change to nonlinear and the Forchheimer equation needs to be used.[15] This new relationship between pressure drop and permeability is shown in Eq. [8].

$$ \frac{\Delta P}{\Delta L} = \frac{\mu u}{K} + \rho Cu^{2}, $$
(8)

where \( \rho \) is the density of the fluid, and \( C \) is the Forchheimer’s coefficient, or form drag coefficient.

In this study, the fluid flow is considered to be in the Forchheimer’s regime. Equation [8] was therefore used to determine permeability, \( K \), and form drag coefficient, \( C \), from the pressure drop values.

Heat Transfer Coefficient

The heat flux and heat transfer coefficient in the LCS porous copper is related by Newton’s cooling law given in Eq. [9].

$$ J = h\left( {T_{b} - T_{in} } \right), $$
(9)

where \( J \) is the input heat flux, \( h \) is the heat transfer coefficient, \( T_{\text{b}} \) is the temperature at the contact point between the heat source and the LCS porous copper, and \( T_{\text{in}} \) is the temperature of the water at the inlet. In this study, Eq. [9] was used to determine the heat transfer coefficient, h, from the temperature of the heat block.

Results and Discussion

Pressure Drop

The relationship between pressure drop and Darcian velocity for samples with a pore size of 1000 μm and different porosities is shown in Figure 3. It is clear that the trend is not linear and the form drag coefficient needs to be considered to account for the inertial effects.

Fig. 3
figure 3

Relationship between pressure drop and Darcian velocity for samples with a pore diameter of 1000 μm and different porosities

Full size image

Figure 4 compares the numerical results obtained for pressure drop with experimental data available from Reference 16 for a range of combinations of pore size, porosity, and flow velocity.

Fig. 4
figure 4

Comparison between numerical and experimental pressure drop values for different pore sizes and porosities. The numerical and experimental (in parenthesis) pore sizes are: (a) 400 (250 to 425) μm, (b) 600 (425 to 710) μm, (c) 800 (710 to 1000) μm, and (d) 1000 (1000 to 1500) μm

Full size image

The numerical results have the same trends as the experimental data and show good agreement with the experimental values for most porous structure and flow conditions. However, there exist significant differences between the numerical and experimental results, especially for low porosity conditions. These differences are partly due to the different porous structure parameters used. In the numerical simulation, a fixed pore size and a fixed porosity are used. The experimental values, however, were obtained for a porous sample with a range of pore sizes and a measured porosity deviated from the numerical condition. Another cause for the differences is the simplification of the porous structure with a unit cell. In the unit cell, each pore or sphere is connected with 12 pores. The actual number of contacts in the LCS porous metals, however, is often much lower[13] and decreases with decreasing porosity as shown in Eq. [2].

Permeability and Form Drag Coefficient

Figures 3 and 4 show that, in all cases, the pressure drop increases quadratically with Dacian velocity, indicating applicability of the Forchheimer Eq. [8]. In order to obtain permeability, \( K \), and form drag coefficient, \( C \), from the numerical results, Eq. [8] can be rearranged to give a linear relationship between \( \Delta P \) and \( u \) in the form of Eq. [10].

$$ \frac{\Delta P}{\Delta L \cdot u} = \frac{\mu }{K} + \rho Cu. $$
(10)

The values of \( K \) and \( C \) were thus obtained by linear regression of the numerical data to Eq. [10].

The variations of permeability and form drag coefficient with porosity, obtained from the numerical results, are shown in Figures 5(a) and (b), respectively. It is shown that both pore size and porosity have significant effects on permeability and form drag coefficient. As expected, permeability increased with porosity whereas form drag coefficient decreased with porosity, because less frontal surface area in the solid material generates less drag force against the fluid.

Fig. 5
figure 5

Relationships between (a) permeability and porosity and (b) form drag coefficient and porosity

Full size image

In the literature, the form drag coefficient is sometimes defined in terms of permeability and a drag force coefficient[17] as in Eq. [11].

$$ C = \frac{{C_{\text{f}} }}{\sqrt K }, $$
(11)

where \( C_{\text{f}} \) is the drag force coefficient.

Figure 6 shows the log–log plots between form drag coefficient and permeability. The form drag coefficient increases with pore size, but the slope of the logC vs logK curve decreases with pore size. It is clear that the data in the current study do not follow Eq. [11], but can be described in the form of Eq. [12].

Fig. 6
figure 6

Relationship between form drag coefficient and permeability

Full size image
$$ C = C_{\text{f}} K^{{ - {\text{m}}}}, $$
(12)

where m is a constant for any fixed pore size.

The values for the exponential term and drag force coefficient for different pore sizes, obtained from linear regressions of the data in Figure 6, are presented in Table II. The value of the exponential term \( m \) is not constant, but it decreases and approaches 0.5 when pore size is increased. The drag force coefficient also increases with pore size.

Table II Exponential Term and Drag Force Coefficient
Full size table

Heat Transfer Coefficient

The relationships between heat transfer coefficient and water flow rate for the porosities of 50 and 80 pct are shown in Figures 7(a) and (b), respectively.

Fig. 7
figure 7

Heat transfer coefficient of REVs with a porosity of (a) 50 pct and (b) 80 pct

Full size image

It can be seen that the heat transfer coefficient increased rapidly with flow rate. The effect of pore size can be seen here as well. Although at low flow rates the effect of pore size was negligible, at higher flow rates, \( h \) was increased by about 5 to 8 pct when pore size was decreased.

The relationships between the heat transfer coefficient and the porosity for pore sizes of 400 and 1000 μm are shown in Figures 8(a) and (b), respectively. A linear relationship exists between the heat transfer coefficient and porosity for all flow rates. At all cases, the best heat transfer coefficient was achieved with higher flow rates. Once again, it can be seen that pore size has little influence on the heat transfer coefficient.

Fig. 8
figure 8

Heat transfer coefficient of REVs with pore size of (a) 400 μm and (b) 1000 μm

Full size image

Conclusions

This paper presented a 3D geometric model for numerical simulation of liquid flow and heat transfer in open-cell porous media. The representative elementary volume was created based on the face-centered-cubic arrangement of spheres linked by cylinders. Different combinations of pore parameters including porosity (50 to 80 pct), pore size (400 to 1000 μm), and fluid flow rate (0.2 to 1.8 l/min) were studied using the software ANSYS Fluent. The numerical results on the pressure drop agreed reasonably well with the experimental data for the LCS porous copper and followed the Forchheimer equation. The numerical results showed that permeability increased whereas the form drag coefficient decreased with porosity. Both permeability and form drag coefficient increased with pore size. The form drag coefficient was related to permeability and the relationship can be expressed by the drag force coefficient and an exponential term. The drag force coefficient increased, whereas the exponential term decreased, with pore size. Heat transfer coefficient increased with flow rate but decreased with porosity. Pore size had very little effect on heat transfer coefficient.