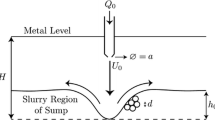
Abstract
With an increase in demand for aluminum alloys, industrial suppliers are seeking to increase the size and speed of casting processes. Unfortunately operating the existing Direct-Chill (DC) process in such conditions tends to enhance metallurgical defects. Perhaps the most recognized of these defects is macrosegregation, whose effects are permanent once the material is solidified. In order to facilitate the expansion of the DC process without increasing the presence of macrosegregation, a novel jet mixing method to distribute the liquid metal is presented. The governing equations for this process are derived and the operating parameters necessary to minimize the centerline macrosegregation are predicted. The results of commercial-scale tests are presented, validating the predictive equations and performance of this process.




Similar content being viewed by others
References
The Aluminium Association, Aluminum Industry Technology Roadmap, The Aluminium Association, Washington D.C., May 1997.
L. Swartzendruber, L. Ives, W. Boettinger, S. Covcill, D. Ballard, D. Laughlin, R. Clough, F. Biancello, P. Blau, J. Cahn, R. Mehrabian, G. Free, H. Berger and L. Mordfin. Report PB81-172348, National Bureau of Standards, National Measurement Lab. Washington D.C., December 1980.
L. Ives, L. Swatzendruber, W. Boettinger, M. Rozen, S. Ridder, F. Biancello, R. Reno, D. Ballard, R. Mehrabian. Internal Report 83-2669. National Bureau of Standards. Washington D.C., January 1983.
D.G. Eskin: Physical Metallurgy of Direct-Chill Casting of Aluminum Alloys, CRC Press, Boca Roton, FL, 2008.
M.C. Flemings: ISIJ Intern., 2000, vol. 40, pp. 833–841.
S.R. Wagstaff and A. Allanore: Light Metals, TMS, 2015, pp. 877–82.
H. Yu, D.A. Granger, Int. Conf. Aluminum Alloys—Their Physical and Mechanical Properties, Charlottesville, VA. EMAS, Warley (U.K.), 1986, pp. 17–29.
M.G. Chu, J.E. Jacoby: Light Metals, TMS, 1990, pp. 925–30.
S.M. Voronov. Z. Metallkde., 1929, vol. 21, p. 310.
A. Håkonsen, D. Mortensen, S. Benum, H.E. Vatne: Light Metals, TMS, 1999. pp. 821–27.
D.G. Suyitno, D.G. Eskin, V.I. Sevran, L. Katgerman: Metall. Mater. Trans. A, 2004, vol. 35A, pp. 3551–3561.
D.G. Eskin, V.I. Savran, L.Katgerman: Metall. Mater. Trans. A, 2005, vol. 36A, pp. 1965–1976.
R.K. Nadella, D.Eskin, L.Katgerman: Continuous Casting of Non-ferrous Metals, Neu-Ulm, Germany, Weinheim: Wiley-VCH, 2005, pp. 277–282.
P.Thevoz, J.L. Desbioles, M.Rappaz: Metall. Trans. A, 1989, vol. 20A, pp. 311-22.
B. R. Morton, G. I. Taylor, and J. S. Turner: Proc. R. Soc. London, 1956, Ser. A 234, pp. 1–23.
B. R. Morton, J. Fluid Mech., 1959, vol. 5, pp. 151–163.
N. Kaye: Atmos.-Oceans., 2008, vol. 46, pp. 433–441
A. Myhr and O. R. Hakonsen: Cast Metals, 1995, vol. 8, pp. 147-157.
R. J. Munro, N. Bethke, and S. B. Dalziel: Phys. Fluids, 2009, vol. 21, 046601.
J.F. Richardson, W.M. Zaki: Trans. Instn Chem. Engrs., 1954, vol. 32, pp 35.
L. van Rijn: J. Hydraul. Eng., 1984, vol. 110, pp. 1431–1456.
K. Mazurek and T. Hossain: Can. J. Civ. Eng., 2007, vol. 34, pp. 744-751.
H. Kobus, P. Leister & B. Westrich: J. Hydr. Res., 1979, vol. 17, pp. 175–192.
J.R. David (ed.): ASM Specialty Handbook-Aluminum and Aluminum Alloys. ASM International. Materials Park, OH. 1993.
S.R. Wagstaff, and A. Allanore: Light Metals, TMS, 2016, pp. 715–20.
A. Shields: Anwendung der Aehnlichkeitsmechanick und der Turbulenzforschung auf die Geschiebebewegung, Mitt. Preuss. Vers. Wasser. Schiff., 1936.
B. M. Sumer, L. H. C. Chua, N.-S. Cheng, and J. Fredsøe: J. Hydraul. Eng., 2003, vol. 129, pp. 585–596.
S. A. Miedema: J. Dredging Eng., 2012, vol. 12, pp. 1–49.
S. A. Miedema: J. Dredging Eng., 2012, vol. 12, pp. 50–92.
B. Gomez: Earth-Sci. Rev., 1991, vol. 31, pp. 89–132.
Y. Niño, F. Lopez, and M. Garcia: Sedimentology, 2003, vol. 50, pp. 247–63.
Acknowledgments
The authors thank the Novelis Solatens Technology Center for their invaluable assistance in completing the present work, and their continuous support.
Author information
Authors and Affiliations
Corresponding author
Additional information
Manuscript submitted March 29, 2016.
Appendices
Appendix 1
\( \alpha \) | Entrainment Constant (0.08) | \( n_{ \hbox{max} } \) | Maximum Number Density of Grains |
|---|---|---|---|
\( \Delta T \) | Undercooling | \( N \) | Nucleation source term |
\( \Delta T_{N} \) | Mean undercooling | \( Q \) | Volume flux of grains |
\( \Delta T_{\sigma } \) | Standard deviation of undercooling | \( Q_{0} \) | Volumetric flow rate |
\( \kappa \) | von Kármán constant (0.41) | \( \tilde{Q} \) | Non-dimensional particle flux per unit width |
\( \nu \) | Kinematic viscosity (5.5 × 10−7 m2 s−1) | \( r_{0} \) | Crater radius |
\( \rho_{f} \) | Fluid density | \( Re_{g} \) | Grain Reynolds number |
\( \rho_{g} \) | Grain density | \( Re_{j} \) | Jet Reynolds number |
\( b_{0} \) | Nozzle radius | \( Re_{m} \) | Mold Reynolds number |
\( C \) | Composition | \( Rs \) | Rouse number |
\( C_{0} \) | Furnace composition | \( Rs_{c} \) | Critical Rouse number |
\( C_{v} \) | Volume fraction of grains | Sh | Shields parameter |
\( d \) | Grain diameter (<70 µm) | Shc | Critical Shields parameter |
\( h_{0} \) | Depth of bed | \( u_{t} \) | Velocity through control volume |
\( H_{0} \) | Depth of fluid and bed | \( u_{*} \) | Shear velocity |
\( m \) | Exponential constant | \( U_{0} \) | Velocity of jet at nozzle |
\( M_{l} \) | Mold length | \( U_{\text{c}} \) | Casting Speed/Crater descent speed |
\( M_{w} \) | Mold width | \( U_{j} \) | Velocity of jet at bed |
\( MI \) | Macrosegregation Index | \( U_{s} \) | Stokes settling velocity |
\( n \) | Number density of grains | \( U_{\text{th}} \) | Hindered settling velocity |
Appendix 2
In studies of uniform, statistically steady turbulent flow over a granular bed, the suspension and transport of particles is generally characterized by the Shields parameter, Sh, representing the ratio of shear stress due to fluid flow relative to the weight per area of individual grains inside the bed.[26] This has been displayed below in Eq. [20], where U is the characteristic flow velocity, d g, grain diameter, and ρ f and ρ g the fluid and grain densities, respectively.
Transport of grains occurs if the Shields parameter exceeds a critical value, which depends on grain size, shape, cohesion, and buoyancy.[27–29] This critical Shields parameter can be difficult to determine experimentally,[30,31] partially because the physical mechanism for resuspension occurs transiently due to turbulent fluctuations.
An alternative classification of granular resuspension and sedimentation is expressed by the Rouse number, Rs, which is proportional to the ratio of the settling speed of the grains, and the turbulent shear velocity of the bed. This relation is expressed below in Eq. [21] where \( u_{*} \) is the shear velocity, \( \kappa = 0.41 \) is the von Kármán constant, and \( U_{\text{s}} \) is the terminal settling velocity of the grains.
Below a critical value of Rs, the flow is capable of maintaining grains in suspension because turbulent velocity fluctuations are larger than the terminal velocity of each grain. In unidirectional, steady flow, full bed transport is anticipated for \( Rs \le 2.5 \), and significant resuspension occurs if \( Rs \le 1 \). Unlike the Shields number, the Rouse number accounts for the influence of viscosity upon each particle through the value of its respective settling speed, \( U_{s} \). For very small grains (<70 μm in the aluminum system) \( U_{\text{s}} \) is given by the Stokes settling velocity, \( U_{s} \).
The granular Reynolds number \( (Re_{\text{g}} ) \) is most usefully defined using \( U_{\text{s}} \) as the characteristic velocity, thereby forming:
where \( d_{\text{g}} \) is the grain diameter, and \( \upsilon \) is the kinematic viscosity (generally assumed to be approximately 5.5 × 10−7 m2/s for molten aluminum).
Rights and permissions
About this article
Cite this article
Wagstaff, S.R., Allanore, A. Minimization of Macrosegregation in DC Cast Ingots Through Jet Processing. Metall Mater Trans B 47, 3132–3138 (2016). https://doi.org/10.1007/s11663-016-0718-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11663-016-0718-6