Surface Tension Measurements of Calcia-Alumina Slags: A Comparison of Dynamic Methods

Abstract

The surface tension of oxide melts is difficult to measure. Even for binary slags with a low degree of polymerisation such as calcia-alumina, there seems no benchmark value for the surface tension available. Published data exhibit considerable scatter even for similar compositions which prevents to build a reliable and consistent database of frequently used physical properties. This study presents an attempt to use three different measurement techniques in the same high-temperature furnace to obtain the surface tension of a binary calcia-alumina slag close to eutectic composition, namely the drop weight method, the pendant drop method, and, for the first time, the oscillating jet method (for circular and elliptic jets) as a function of temperature. The methods used in the present context are explained, and the experimental results evaluated with respect to previously published data. A consistent and coherent trend is observed when the drop weight and the oscillating jet methods are compared.

Introduction

Surface tension is a fundamental property which has manifestation in all surface and interfacial phenomena. For example, the surface and interfacial tension affect droplet size and drop size distribution via droplet breakage and coalescence behavior, which is important in heavily stirred reactors in process metallurgy to control reaction rates. Moreover, surface active components may have a strong effect on the surface tension and may impose considerable surface tension gradients which give rise to Marangoni effects.

The surface tension of slags and steel or the interfacial tension between them plays a dominant role in iron- and steelmaking processes as their absolute values are about 5 to 20 times larger than those of water.[1] Generally, the surface tension of pure oxides and slags (200 to 700 mN m⁻¹) is lower than the surface tension of metals, but their viscosities are usually far higher and strongly increase with decreasing temperatures.

Compared with dynamic viscosity, the surface tension of slags has not yet been investigated in such detail, resulting in more scatter of experimental data.[2] However, considerable amounts of experimental data have been collected for different systems at various compositions and temperatures; see for example the review by Mills and Keene.[3] From the analytical point of view, predictive models have been developed,[4–7] nevertheless, there often seem to be discrepancies between predicted values and experimental data which underline the need for a more reliable experimental database.

In principle, a broad variety of surface tension measurement techniques is available. However, due to the special conditions in high-temperature environments, the technique employed should be appropriate for the experimental conditions.[8] This is why most of the measurements have been carried out using one of the following: sessile drop method, pendant drop method, drop weight method, maximum bubble pressure method, cylinder and ring detachment method. A survey and description of suitable methods for high-temperature systems has been given by Keene[8] and Korenko and Šimko.[9]

It is an unfortunate matter of fact that there are considerable deviations among the experimental data. These may originate from the presence of uncontrolled surfactants at the surface, from uncertainties in the density value at a given temperature and composition, and from the uncertainty whether the system was in equilibrium or not since chemical reactions and surfactant adsorption have a strong dynamic impact on the surface tension. Similarly, the surface tension depends strongly on the atmosphere used in the experiments. For example, the surface tension of a 40 pct CaO-40 pct SiO₂-20 pct Al₂O₃ slag under nitrogen can be much higher than the same slag under hydrogen or ammonia. Likewise, the container material has an effect due to reaction kinetics, wetting behavior, etc.[8] Hence, in order to facilitate comparative studies, all materials and fluids being in contact with the molten sample should be specified and named properly.

In each case, the measurement technique chosen for a particular experiment determines which uncertainty factor is more dominant. Even for seemingly simpler binary systems without complex interactions within the ionic structure such as calcia-alumina, the scatter can be considerable, as can be seen in Figure 1 (see also corresponding details in Table I). Indeed, the question needs to be asked if there will ever be a distinct benchmark value available for a given composition and temperature combination to compare different sets of data against (as is available for water, for example).

Fig. 1

Surface tension for calcia-alumina slag close to the eutectic composition as a function of temperature. Compilation of data reported by different authors [10,13–21] using different methods. MBP, maximum bubble pressure; SD, sessile drop; PD, pendant drop; SM, slide method. See also Table I for more details

Table I Details of Surface Tension Measurements from References Mentioned in Fig. 1

In this paper, three different measurement techniques, namely the drop weight method, the pendant drop, and the oscillating jet method for circular and elliptic jets were used to measure the surface tension of a calcia-alumina slag close to the eutectic composition at high temperatures. For this purpose, a high-temperature visualisation facility using a high-speed camera has been developed. A droplet generating device made entirely from graphite produces either single droplets or coherent jets within a long hot zone furnace flushed with ultra-high purity argon featuring horizontal optical access through a quartz window embedded in an alumina protection cross-tube assembly. An attempt was made to assess the accuracy, merit and shortcomings of each method in the framework of high-temperature experiments.

Materials and Methods

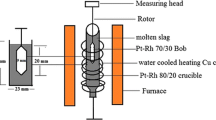
All measurements described here were performed in the same high-temperature furnace as has been described elsewhere.[10–12] The design allows different surface tension measurement techniques, namely the drop weight method (DWM), the pendant drop method (PDM), the oscillating jet (OJM), and the elliptic jet method (EJM) to be adapted. For the first two, we used a slow dripping method in which droplets are allowed to detach from a circular knife-edged graphite capillary at low volume flow rates. Dripping is required for the drop weight method, whereas the pendant drop method usually requires static conditions to establish equilibrium of forces. However, it was shown in an earlier paper that the method could be used in the slow dripping regime.[10]

For the oscillating jet method, the orifice exit velocity of the liquid should be high enough to form a jet, but low enough to be within the Rayleigh (or laminar) regime. The jet diameter should be relatively small compared to the wavelength of the oscillation.[22] The flow rate can be increased by pressurising the crucible chamber with argon. Two different graphite orifices have been used: a 1-mm circular opening and an elliptic nozzle with the major and minor axes of 4 and 1 mm, respectively.

The experimental unit consisted of the electrically heated three-zone tube furnace with an alumina cross-tube assembly for optical access and atmosphere control, the graphite droplet generating assembly, the Phantom v3.11 high-speed camera, and the pneumatic turbine vibrator to impose an external excitation on the jets.

A synthetic calcia-alumina slag was prepared, aiming for its composition to be close to the eutectic composition. The oxides were prepared in the following manner: calcination of CaCO₃ to CaO and removal of moisture at 1273 K (1000 °C) in alumina crucibles; mixing of powders on a roller mixer for 24 h; melting of powders in a muffle furnace using a 95 pct platinum/5 pct rhodium crucible with subsequent quenching in an inclined steel launder; and finally crushing. The chemical composition was analyzed by X-ray fluorescence (XRF) measurements. Table II shows the details. No other components than calcia and alumina have been detected. During all experiments, the slag was in contact with graphite only. The flushing and pressurising gas was ultra-high purity argon.

Table II Specification of Chemicals Used for Sample Preparation

It is beyond the scope of this paper to give a comprehensive review of each surface tension measurement method employed here. Instead, only a brief description is given in the Section III with the main equations and concepts as far as they have been used in our experiments. For detailed reviews, we refer the reader to further literature, in particular a more recent review for high-temperature systems by Korenko and Šimko.[9]

Results and Discussion

Drop Weight Method

The drop weight (or drop volume) method is a widely used method to determine the surface or interfacial tension in low-temperature systems. In high-temperature systems, however, this method is not as common as for instance the maximum bubble pressure method. The drop weight method appears to be rather simple, but it requires knowledge of the main errors which might occur from choosing the drop weight correction factors, the operating parameters, hydrodynamic effects, the behavior of the liquid at the capillary and many more. For example, the capillary material should be preferably non-wetting, the drop formation time should be larger than 30 s to reduce hydrodynamic effects, the number of droplets to be analyzed for statistical reliability should be around 30, and the length to diameter ratio of the capillary $L_{\text{cap}} /D_{\text{cap}}$ should satisfy $L_{\text{cap}} /D_{\text{cap}} > 0.035Re$ to ensure fully developed laminar flow.[23] Comprehensive reviews can be found elsewhere.[23]

In principle, the drop weight method reflects the fact that a drop detaches from a capillary when the gravitational force $M_{\text{P}} g$ is no longer balanced by the surface tension $\sigma$. In reality, however, not all of the liquid will form the drop, and a certain volume remains at the capillary tip. Hence, the force balance involving surface tension $\sigma$, gravity g and capillary radius $R_{\text{cap}}$ has to be modified by a drop weight correction factor $\Psi$:

$$ M_{\text{P}} g = 2\pi R_{\text{cap}} \sigma \Psi $$

(1)

The most commonly used correction factor is the one published by Harkins and Brown[24] which itself is a function of the capillary radius $R_{\text{cap}}$ and the cubic root of the detached drop volume $V_{\text{P}}$: $\Psi \left({\chi}\right)\varvec{ }$with ${\chi}= {R}_{\text{cap}} V_{\text{P}}^{ - 1/3}$. Lee et al.[25] proposed a polynomial equation to calculate the Harkins and Brown correction factor, the so-called LCP (Lee-Chan-Pogaku) model:

$$ \begin{aligned} \Psi \left( \chi \right) = & 1.000 - 0.9121\chi - 2.109\chi^{2} + 13.38\chi^{3} - 27.29\chi^{4} \\ & + 27.53\chi^{5} - 13.58\chi^{6} + 2.593\chi^{7} \\ \end{aligned} $$

(2)

However, as pointed out by Lee et al.,[23] the validity range is limited and was extended by numerous investigators resulting in a multitude of different models for the correction factor, examples listed in Table I in Lee et al.[23] Especially for liquid metals (high surface tension) with $\chi < 0.35$, the discrepancies may be substantial.

Contradictory statements were made with regards to the influence of the viscosity of the liquid. Some are suggesting modifying Eq. [1] by a correction function taking into account drop formation time and kinematic viscosity, whereas in other works the viscosity seems not to have any effect on the Harkins and Brown correction factors for viscosities up to 10 Pas.[25] Hence, the usefulness of the method also depends on the right choice of the correction factor, but the open question remains which one. This introduces an uncertainty, especially in high-temperature experiments where benchmark values are not available, as pointed out in Section I.

Yildirim et al.[26] developed a more theoretically founded relationship derived from computations of droplet formation dynamics between the dimensionless volume of the detached droplet and the Weber, Bond and Ohnesorge number ($We = \rho Q^{2} \pi^{ - 2} R_{\text{jet}}^{ - 3} \sigma^{ - 1}$, $Bo = \rho gR_{\text{jet}}^{2} \sigma^{ - 1}$, $Oh = \mu \left( {\rho R_{\text{jet}} \sigma } \right)^{ - 1/2}$, respectively). For vanishingly small Weber numbers (which implies a small flow rate) and Ohnesorge numbers preferably below unity (which implies a relatively low viscosity), the best-fit correlation obtained by the authors was

$$ Bo = 3.60\chi^{2.81} $$

(3)

For the drop weight method, in any case, the capillary radius and the volume of the detached droplet must be known in both Eqs. [1] and [3] in order to calculate the surface tension. In high-temperature experiments, the thermal expansion of the capillary has to be taken into consideration and can be determined with optical measurements (comparison of reference image of the capillary at ambient temperature and image at experimental temperature). Regarding the volume of a falling droplet, there are basically two ways to determine $V_{\text{P}}$: (1) one can measure the mass per droplet using a balance and calculate the volume if the slag density is known, or, since the density is not necessarily known exactly and is subject to a relatively large error, one can (2) approximate the volume by image analysis. This is not a trivial task if only the projection of the silhouette in the vertical x,z-plane is available. For this case, Hugli and Gonzalez[27] discussed several volume estimation methods which all assume rotational symmetry of the liquid body. The best performance was obtained if one integrates over the volume of slices of spherical disks with thickness $\Delta y$ and surface area $\left( {\pi /4} \right)d^{2} \left( y \right)$, see Figure 2(a). The smaller one chooses $\Delta y$, the more accurate the result will be. This method was implemented in the image analysis software used in the present study with the disk height $\Delta y$ corresponding to one pixel of the analyzed image equivalent to approx. 58 µm for a droplet of approx. 6.5 mm. This method also allows measuring the density as shown in the following section, as the volume and the mass of a single droplet are now known.

Fig. 2

(a) Arbitrary rotational symmetric shape model.[27] Schematic of volume determination of a liquid body in the x, z-plane assuming rotational symmetry. In contrast to the ellipsoidal shape model, the liquid body does not necessarily need to be ellipsoid when using this method. (b) Relevant diameters d _e and d _s required for the selected plane method

Density measurements

In this trial, the slag was heated to three different temperatures, 1808 K (1535 °C), 1858 K (1585 °C), and 1908 K (1635 °C). A 3 mm ID graphite capillary has been used. The drop dripping frequency was kept low enough to ensure that the balance captured the individual weight of each droplet. The drop weight—and hence the drop formation and detachment—was found to be highly repetitive. The droplet formation and their fall after detachment were recorded with the high-speed camera at 5000 fps. In post-processing, the volume of the detached falling and slightly oscillating droplet was calculated for each frame (hence as a function of time) in five different ways. For each case rotational symmetry was assumed:

• 1. corresponding sphere volume $\pi /6d_{\text{P,vert}}^{3}$using the vertical diameter of the falling droplet ($d_{\text{P,vert}}$ corresponds to the height of the falling droplet),

• 2. corresponding sphere volume $\pi /6d_{\text{P,hori}}^{3}$ using the horizontal diameter of the falling droplet ($d_{\text{P,hori}}$ corresponds to the width of the falling droplet),

• 3. corresponding ellipsoid volume $\pi /6d_{\text{P,vert}}^{2} d_{\text{P,hori}}$,

• 4. corresponding ellipsoid volume $\pi /6d_{\text{P,vert}}^{{}} d_{\text{P,hori}}^{2}$, and

• 5. slice method as depicted in Figure 2(a) and previously explained.

Figure 3(a) shows the results of the volume of a slag droplet at 1808 K (1535 °C) as a function of time calculated using the five methods. The first four methods give calculated drop volumes that vary considerably with time (roughly 2.5 pct, and even greater in the early stages). By contrast, the slice method yields relatively constant values of drop volume from the point of droplet detachment ($t = 0$). Here, the variation was within ±0.4 pct. Figure 3(b) compares the slag density obtained using the ellipsoid approximation with the slice method. Again, the slice method gives fairly good results with much smaller scatter over the whole time range.

Fig. 3

(a) Volume as a function of time of a falling and oscillating slag droplet at 1808 K (1535 °C), calculated using fie different methods (see text for details). (b) Corresponding slag density. Comparison of slice method with ellipsoid approach and literature data

For comparison, density values interpolated to 1808 K (1535 °C) from experimental data reported by Sikora and Zielinski[28] (50/50 wt pct calcia-alumina slag) are also given. The authors used molybdenum as capillary and crucible material in argon atmosphere and applied the maximum bubble pressure method to measure surface tension and density. The comparison shows that density values obtained by the slice method are in very close agreement with the data by Sikora and Zielinski[28] which are in general on the higher side when compared to other literature data. Table III shows the density results for all three temperatures. The density value for 1858 K (1585 °C) deviates slightly more than the other two (1.2 pct compared to 0.12 and 0.04 pct, respectively).

Table III Density $\rho$, Mean Mass of Droplets $\bar{M}_{P}$, Mean Droplet Volume $\bar{V}_{P}$, $\chi$-value, Correction Factors and Bond Number $Bo$ of the Used Calcia-Alumina Slag at Different Temperatures

Surface tension results

With mass, density, and volume of the detached droplets from the previous section, the correction factor $\Psi$ required in Eq. [1] can be calculated. Some selected correlations from Lee et al.[23] are given in the Appendix which can be used to determine the correction factor, $\Psi \left( \chi \right)$. The evaluated correction factors are listed in Table III based on the $\chi$ value for each temperature. In our case, the values for $\chi$ are around 0.28 for all droplets and temperatures analyzed here, see also Table III. The surface tension is displayed in Figure 4(a) as a function of temperature. As can be seen and as indicated above, the surface tension value depends on the choice of the correction factor. However, except for the Clift equation, the values are all in the same range. The deviation between maximum and minimum for each temperature is below 17 mN m⁻¹, or below 3 pct of the average value. The Clift equation obviously yields a relatively high correction factor which leads to lower surface tension values. However, as indicated in Figure 4(b), the corresponding values are still within the scatter of data compiled from literature values, albeit on the lower side.

Fig. 4

Surface tension of calcia-alumina slag obtained by the drop weight method as a function of temperature. (a) Comparison of values using different correlations for the Harkins and Brown correction factor. (b) The same data as left but embedded in a compilation of literature data (black crosses, cf. Figure 1). The same legend as in (a) applies

Pendant Drop Method

As shown already in a previous paper,[10] the selected plane method with tabulated data reflecting the droplet shape parameters was used to determine the surface tension.[29–32] Bidwell et al.[33] extended the tables to a larger parameter range, taking also droplets with high surface tension (like metals or likewise) into account. Using the selected plane method, the only droplet shape parameters required are the maximum droplet width $d_{\text{e}}$ and the diameter $d_{\text{s}}$ at the height $d_{\text{e}}$ above the droplet tip, see Figure 2(b). The ratio $S = d_{\text{s}} /d_{\text{e}}$ is a function of the physical properties of the liquid. With $S$ one gets the parameter $H^{ - 1}$ which is available in tabulated form in the work by Bidwell et al.[33] With this $H^{ - 1}$ value, the surface tension can finally be calculated with

$$ \sigma = g\rho d_{\text{e}}^{2} H^{ - 1} $$

(4)

The Bidwell data could be approximated with the following power law function:[10]

$$ H^{ - 1} = 0.3143S^{ - 2.6278} $$

(5)

in the range $S = \left[ {0.5 \ldots 0.98} \right]$. A macro procedure in the image analysis tool was developed which extracts the values $d_{\text{e}}$ and $d_{\text{s}}$ for every image. Finally, the surface tension can be calculated as a function of time using Eq. [4]. It should be noted here that the selected plane method is not as accurate as the pendant drop method using a direct fit of the Young–Laplace equation to the drop profile, and hence exhibits relatively large errors. It is interesting to note that the Young–Laplace fitting method has been tested in different laboratories using commercial software, but to no success.[34] The reason is currently unknown and subject to future investigations.

However, for this study, the selected plane method was tested and compared, using the same raw images (and hence the same droplets) which were used for the drop weight method. As explained above, those droplets were slowly dripping from the graphite capillary with constant liquid delivery. Figure 5(a) shows an example of a typical result. The apparent surface tension is plotted as a function of time. There are three distinct regions in the diagram. Only in the middle of the process—where the droplet has reached a suitable length—does the surface tension remain relatively constant before it increases due to the stretching of the droplet which no longer represents equilibrium between gravity and surface tension. In the middle region, an average value can be defined for each droplet investigated, and the mean of all average values can be calculated. In Figure 5(a), the lower and upper dashed lines represent the scatter of this method which was determined to be around ±10 pct for this and the other two temperatures. Figure 5(b) shows the surface tension values obtained by the pendant drop method with 10 pct error bars in comparison to the values obtained by the drop weight method (enveloped region) and those published by other authors (black crosses), cf. Figure 1. While the upper error margin is in good agreement with the drop weight method data, the mean values are in reasonable agreement with our previously published data using the same method but a slightly different composition and a smaller capillary.[10]

Fig. 5

(a) Apparent surface tension as a function of time for a calcia-alumina slag at 1808 K (1535 °C). (b) Surface tension obtained by the pendant drop method (black squares) in comparison to the values obtained by the drop weight method (DWM) and to previously published data as a function of temperature. For the DWM data, the same legend as in Figure 4(a) applies

Oscillating Jet Method

Circular jets

When a column of a liquid, initially of constant radius, is falling vertically under gravity it will decompose into a string of droplets due to capillary instabilities. The initial disturbances which later cause the jet to breakup have to grow in time and space and will modify the jet shape, forming necks and swells whose radii decrease and increase with time, respectively. The disturbances may originate from the jet itself and/or from the surroundings (pumps, fans, etc.).[35]

Instead of repeating the overwhelming amount of work that has been done on the experimental and analytical side to reveal the governing phenomena of liquid jets, we will explain in this section the scheme how the surface tension was extracted from an oscillating jet issuing from a circular graphite orifice, compare also with Figure 6. Similar and different methods have been reported elsewhere, e.g.,[22,36–42] First, a number of real images (say for example 20 consecutive images) of a recorded sequence were loaded into the image analysis software. A macro was written which extracted the coordinates of the jet outline of each image and hence the jet diameter as a function of the axial coordinate $z$ from the capillary tip downwards until drop detachment. In the ideal case, the jet shape or the radial surface displacement of the jet radius can be expressed by[39]

$$ r\left( {z,t} \right) = R_{0} + \varepsilon_{0} e^{\alpha t} cos\left( {kz} \right) $$

(6)

with the undisturbed initial jet radius $R_{0}$, the amplitude of the initial disturbance $\varepsilon_{0}$, the growth rate coefficient or growth factor $\alpha$, the wavenumber $k = 2\pi /\lambda$ ($\lambda$ being the wavelength), and the axial coordinate $z$. Of course, the real jet shape will deviate from the ideal case described by Eq. [6], and instead of forcing to match real and ideal shape, it shall be sufficient to consider the exponential growth of the swell radii, thus omitting the cosine term. Figure 6(a) shows exemplarily $r\left( {z,t} \right)$ with and without the cosine term. If the real jet shape images (as extracted from the recorded sequences) are overlaid, the increase of the jet radii with time becomes apparent, see Figure 6(b). The shape profiles are useful only before the breakup zone is reached in which the jet disintegrates into droplets. In the next step, the maximum value of the radius at each axial position was determined. The logarithm of the difference between the maximum value and the initial radius divided by $\varepsilon_{0}$, $\ln \left[ {\left( {\hbox{max} \left( {r\left( {z,t} \right)} \right) - R_{0} } \right)\varepsilon_{0}^{ - 1} } \right]$was then plotted as a function of time, see the cross symbols in Figure 6(c). In an appropriate time interval, these values form a curve with several local maxima. In a next step, the local maxima were extracted (black dots in Figure 6c), and the least-square method was used to find the best linear equation through the black dots. This step finally gives $\alpha$ and $\varepsilon_{0}$. $\alpha$ is equal to the slope of the linear function in Figure 6(c). With known growth rate $\alpha$, slag density $\rho$, jet radius in unperturbed state $R_{0}$, and wavelength $\lambda$ which was also obtained from the experiments, the surface tension can be calculated via the dispersion relation taking into account the slag viscosity $\mu$:[43]

$$ \sigma = 2\rho R_{0}^{3} \frac{{\alpha^{2} + \alpha \frac{3\mu }{{\rho R_{0}^{2} }}\left( {kR_{0} } \right)^{2} }}{{\left( {kR_{0} } \right)^{2} - \left( {kR_{0} } \right)^{4} }} $$

(7)

Fig. 6

Determination of surface tension from jet experiments. (a) Development of jet shape according to Eq. [6]. (b) Real jet shapes extracted from the recorded sequences. The maximum radius at each axial position was determined and plotted as a function of time, see (c). (c) Determination of instability growth rate $\alpha$ and initial disturbance $\varepsilon_{0}$. The slope of the best fitting linear equation through the maxima of the maxima gives the growth rate. Here: $\alpha = 265\,{\text{s}}^{ - 1}$, $k = 1020\,{\text{m}}^{ - 1}$, $\varepsilon_{0} = 0.839\,\mu {\text{m}}$, $R_{0} = 0.56\,{\text{mm}}$

The surface tension should be independent from the disturbance which initiates jet breakup. Thus, we evaluated a jet which disintegrated in natural breakup mode and in addition a jet which was subject to external perturbation. The details and snapshots of the jets were explained and shown in an earlier paper.[12] Table IV shows the results obtained at a temperature of 1933 K (1660 °C).

Table IV Results of Oscillating Jet Method with and Without External Vibration for a Jet Radius $R_{0}$ of 0.56 mm at 1933 K (1660 °C)

As can be seen, both obtained values for the surface tension are very close to each other. Figure 7 displays these values in comparison to the values obtained from the drop weight method discussed previously (cf. Figure 4). The data show excellent agreement which raises hope to assume that both sets of data represent the surface tension of this slag as a function of temperature in an appropriate manner. In addition, our results are in good agreement with the data reported by Mukai and Ishikawa[19] using the pendant drop method.

Fig. 7

Surface tension of calcia-alumina slag obtained by the oscillating jet method (OJM) and the elliptic jet method (EJM) in comparison to the values obtained by the drop weight method (DWM) as a function of temperature. The pendant drop method measurements have been omitted here for clarity. For the DWM data, the same legend as in Figure 4(a) applies

Elliptic jets

If the liquid is pushed through an orifice with elliptic cross-section, a standing-wave jet is produced. The corresponding theory was developed by Rayleigh[44] and later by Bohr[45] who added among other things the effect of viscosity, but neglected gravity as Rayleigh did. A summary of these theories can be found in the work by Bechtel et al.[46] who themselves developed a more recent integro-differential model to determine the dynamic surface tension of a liquid issuing from an elliptic nozzle into a gaseous environment. In contrast to Bohr’s model, they address the fact that the maximum and minimum dimensions of the cross-section within one wavelength is not constant due to the action of viscosity and gravity. The dispersion relation for different aspect ratios was presented by Amini et al.[47].

However, if one uses the Bohr model, the surface tension can be related to measurable quantities by the following equation[48]

$$ \sigma = K\frac{{4\rho Q^{2} \left( {1 + \frac{37}{24}\left( {\frac{b}{{r_{\text{s}} }}} \right)^{2} } \right)}}{{6r_{\text{s}} \lambda^{2} + 10\pi^{2} r_{\text{s}}^{3} }} $$

(8)

with the liquid density $\rho$, the volumetric flow rate $Q$, the wavelength $\lambda$, the stream radius $r_{\text{s}}$

$$ r_{\text{s}} = \frac{{r_{\hbox{max} } + r_{\hbox{min} } }}{2}\left[ {1 + \frac{1}{6}\left( {\frac{b}{{r_{\text{s}} }}} \right)^{2} } \right] $$

(9)

the amplitude $\frac{b}{{r_{\text{s}} }}$

$$ \frac{b}{{r_{\text{s}} }} = \frac{{r_{\hbox{max} } - r_{\hbox{min} } }}{{r_{\hbox{max} } - r_{\hbox{min} } }} $$

(10)

and a correction factor $K$ which accounts for viscosity:

$$ K = 1 + 2\left( {\frac{\mu \lambda }{{\pi \rho Ur_{\text{s}}^{2} }}} \right)^{3/2} + 3\left( {\frac{\mu \lambda }{{\pi \rho Ur_{\text{s}}^{2} }}} \right)^{2} + \cdots $$

(11)

Similar expressions have been developed, e.g., by Sutherland,[49] Defay and Hommelen,[50] or in an even simpler form as proposed by Burcik.[51] Equation [8] is very similar to the one reported by Kochurova and Rusanov[52] who took into account the density of the surrounding gas (which can be neglected here as $\rho_{\text{slag}} \gg \rho_{\text{gas}}$).

In the present study, we aim to determine the surface tension as if Bohr’s formula were applicable. An elliptical graphite capillary was used with $d_{\hbox{max} } = 4\,{\text{mm}}$ and $d_{\hbox{min} } = 1\,{\text{mm}}$. The capillary was positioned in a way that the long axis was perpendicular to the optical axis. In our case, the jet is highly viscous and quickly retracts to cylindrical shape within two or three wavelengths see Figure 8. Bohr’s equation, however, is only valid if the surface velocity of the jet is equal to the mean velocity, which is only the case after a certain distance from the capillary tip.[22,53] According to Bohr[45] the rate at which differences in the jet velocity profile disappear is equal to $e^{ - \kappa t}$with

Fig. 8

Elliptic slag jet at 1973 K (1700 °C). The graphite capillary used here is shown on the right, indicating its relative position related to the camera

$$ \kappa = \frac{{\mu_{\text{jet}} }}{{\rho_{\text{jet}} }}\left( {\frac{1.2197\pi }{{r_{\text{s}} }}} \right)^{2} $$

(12)

For the present configuration ($\mu_{\text{jet}} = 0.19\,{\text{Pas}}$, $\rho_{\text{jet}} = 2739\,{\text{kg}}\,{\text{m}}^{ - 3}$, $r_{\text{s}} = 0.947\,{\text{mm}}$), the differences in velocity decrease within $t = 5.45\,{\text{ms}}$ by a factor of $1/e^{ - \kappa t} = 538$. One has also to keep in mind that the stationary waves—and hence the surface tension—of an elliptic jet also closely depend on the individual capillary characteristics (material, geometry, etc.). Thus, in the past nozzles were chosen empirically to find the best nozzle giving the most accurate results for water[22], which is of course not convenient in high-temperature experiments.

We produced one jet profile at 1973 K (1700 °C) for one flow rate ($Q = 472.11\,{\text{mL}}\,{ \hbox{min} }^{ - 1}$). Due to limited access to the furnace chamber, it was not possible to record both orthogonal views at the same time, but only one. This forced us to use a linear approximation for the minimum radius at position $z_{1}$ in Figure 8 using the neck radii at the beginning and at the end of this wavelength. Table V shows the parameters required to solve Eq. [8]. Although the assumptions may seem to be quite rough, the surface tension value is surprisingly close to the expected value when compared to the foregoing results from the drop weight and oscillating jet method, cf. Figure 7. The obtained value perfectly coincides with the surface tension reported by Ershov and Popova[14] at that temperature. The drawback of the elliptic jet method used here is the relatively large error bar (approx. ±5 pct), which results from an uncertainty of 1 pixel in the image analysis. However, this error can be reduced using a higher resolution camera in future measurements.

Table V Parameter and Surface Tension Value of Elliptic Jet Method at 1973 K (1700 °C)

A Note on Comparison

The surface tension of a synthetic calcia-alumina slag was measured at high temperatures using different measurement techniques. The scatter among the previously published data is considerable, and it seems that fixed benchmark values are currently not available for molten oxides as the demanding conditions and the sensitivity of the surface tension toward the method, materials, and atmosphere makes it challenging to verify and reproduce data within a reasonable error margin. The idea of this paper was to employ different methods with their respective pros and cons using the same slag. If the data show a consistent trend with temperature for all the methods used then the measurements could be considered reliable.

In this paper, we present data obtained by the drop weight method, the pendant drop method, the oscillating jet method with circular and elliptic cross section of the graphite capillary. Overall, good agreement was observed among the data. For the drop weight method, the density had to be determined from the silhouettes of the detached droplets (which gave the volume) and the weight of each droplet. Excellent agreement was found with published density data by Sikora and Zielinski[28] when the slice method was used to approximate the droplet volume. The drop weight method itself showed a consistent trend with temperature. The distinct surface tension value, however, depended on the choice of the Harkins and Brown correction factor. It was found that the models by Gunde and Hartland, Zhang and Mori, Deshiikan et al. and the LCP model by Lee et al. (see Appendix and Reference 23) yielded comparable results. The Bo-equation by Yildirim et al.,[26], Eq. [3], gave values on the upper end, but it was still in good agreement with the aforementioned. Only the Clift-equation should be used with care. The results obtained by the drop weight method were in good agreement with the data reported by Mukai and Ishikawa.[19]

The selected plane method was used for a pendant drop to calculate the surface tension. The droplets were allowed to grow constantly but slowly as still droplets are very difficult to obtain at high temperatures. This method exhibited a relatively large uncertainty of ±10 pct due to the fact the one has to determine the ratio of two geometry values obtained from the images which both have an inherent error of one pixel. The mean values were lower than those obtained by the drop weight method, but in good agreement with our previously published data Wegener et al.[10] and those reported by Zielinski and Sikora.[18]

For the first time, the oscillating jet method was tested for molten oxides at high temperatures. Two different graphite capillaries were used, one with circular and one with an elliptical cross-section. Due to the demanding experimental difficulties, only results from two temperatures were shown here. For the circular jet, the instability growth rate was measured from the maxima of the jet radii which grow in time. Both a jet subject to natural disturbances and an externally perturbed jet were examined, both gave similar growth rates but with different amplitudes of the initial perturbation. The surface tension values were obtained using the dispersion relation which takes viscosity into account. By contrast, the elliptic jet produces a standing wave if the jet exit velocity is high enough. No additional perturbation is required. A high-speed camera would not have been necessary. However, the Bohr model which is used to calculate the surface tension requires the minimum and maximum radii of the jet at the same axial position but from both orthogonal views which was not possible in the present furnace. Hence, a linear approximation was used here. Another drawback of this method is that the jet quickly recovers to cylindrical which resulted in a limited number of necks and swells usable for analysis. However, both methods showed excellent agreement in surface tension values to the expected trend obtained from the drop weight method.

Conclusions

The surface tension of a calcia-alumina slag close to eutectic composition was measured at high temperatures using different measurement techniques, namely the drop weight method, the pendant drop method, and for the first time in high-temperature experiments the oscillating jet method using both circular and elliptic capillaries. The overall conclusion of this work is that the drop weight method and the oscillating jet method with circular orifice provide the most reliable measurements for molten oxides at high temperatures because they generate the most consistent values of surface tension within the range of temperatures studied. The uncertainty in the experiments was reasonably low for the drop weight and the oscillating jet method and did not exceed ±2 pct. The error is more significant when using the pendant drop and the elliptic jet method due to access restrictions and the fact that one has to rely one few measurement points. Also, the image resolution can be further increased in future measurements to minimise errors based on image analysis.

Within the scientific community, considerable efforts should be made to initiate a wider inter-comparison study which should involve the most promising techniques to benchmark the surface tension of slags. As the materials and gases play an enormous role, a standard reference material should be defined in order to facilitate comparative studies.

Appendix

Equations as reported in Lee et al.:[23]

Clift et al., $0 \le \chi \le 0.3$:

$$ \Psi \left( \chi \right) = 1.000 - 0.66031\chi + 0.33936\chi^{2} $$

(A1)

Gunde and Hartland, $0 \le \chi \le 1.2$:

$$ \Psi \left( \chi \right) = 0.99998 - 1.561285\chi + 3.131809\chi^{2} - 4.048916\chi^{3} + 2.849794\chi^{5} - 0.761799\chi^{4} $$

(A2)

Zhang and Mori, $0 \le \chi \le 0.95$:

$$ \Psi \left( \chi \right) = 0.6 + 0.4\left( {1 - \chi } \right)^{3} $$

(A3)

Deshiikan et al., $0 \le \chi \le 0.81$:

$$ \begin{aligned} \Psi \left( \chi \right) = & 1.038438912 - 1.1053622657\chi + 0.06414365\chi^{2} + \\ 3.541869215\chi^{3} - 5.4125444873\chi^{4} - 2.5753239453\chi^{5} \\ \end{aligned} $$

(A4)