Introduction

The nitriding and carbonizing of surfaces are well-known methods for improving tribological properties of different metallic compounds, in particular, of titanium and its alloys. The established methods of metals surface treatments are plasma and gas nitriding.[1] The linked processes, mainly diffusion, have been described by many authors. They are based on the diffusion-like process of the nitrogen in the matrix in millisecond time regimes. Alternatively, it is possible to treat the surface with laser radiation, to synthesize hard coatings directly; in general, this has been done by Nd:YAG[2] and CO2[3] lasers. In this work, coatings several microns in thickness were synthesized. In other experiments,[4,5] TiN coatings were generated for the first time by means of a free electron laser (FEL). Due to its high power and the flexibility in its temporal shaping, this type of laser could be the right tool. The coatings show quite good tribological properties such as hardness. In order to understand the various physical processes, it is necessary to make in-situ investigations. The nitrogen transport and corresponding coating properties are determined by the time of treatment, for which diffusion will be assisted by the Marangoni convection for extended time regimes. The film thickness mainly depends on the melting depth and the nitrogen profile resulting from the ratio of the diffusive and convectional transport.

The modeling of similar laser treatments is thoroughly discussed in the literature; different approaches are available for describing processes such as welding, deep penetration welding, drilling, cladding, and alloying. It is sometimes necessary to use moving interface approaches to describe the physics of the conditioning. Different numerical models could be used to describe the physics of gas-liquid interfaces, especially for laser melt pools; the volume-of-fluid,[6] Lagrangian–Euler,[7] and level set[8] methods are among the most popular. The latter method was used to describe the keyhole development of iron treatment,[9] the cladding of stainless steel,[10] and solidification.[11]

Theoretical Background

Beam Properties of FEL

Experiments were performed at the Jefferson Lab (Thomas Jefferson National Accelerator Facility, Newport News, VA). The FEL operates like a synchrotron and can be adjusted in different time regimes and wavelengths. Detailed information is available in Benson et al.[12] Figure 1 shows the temporal pulse structure in a continuous wave mode. It is a sequence of approximately 200-fs pulses with a frequency of approximately 4.7 MHz. Alternatively, it is possible to switch to the pulsed mode with macropulses of some hundreds of microseconds full width at half maximum (FWHM) at frequencies of 10 to 60 Hz. That setup was used in other investigations.[4]

Fig. 1
figure 1

Gaussian-like time shape of a micropulse at the time t 0 = 10 ps (FWHM 0.2 ps)

Full size image

The wavelength λ during the material processing was 1.64 microns. Equation [1] describes the Gaussian-like shape of a pulse in a Cartesian system (x,y,I). The raw beam approximately 6 cm in diameter was focused to a spot size of approximately 600 μm:

$$ I_{\text{mic}} \left( {t,x,y} \right) = I_{{0{\text{mic}}}} \exp \left[ {\frac{{ - \left( {x^{2} + y^{2} } \right)}}{{2\sigma_{d}^{2} }}} \right]\,{\cdot}\,\exp \left[ {\frac{{ - \left( {t - t_{0} } \right)^{2} }}{{2\sigma_{t}^{2} }}} \right] $$
(1)

  • spatial: \( \sigma_{d} = \frac{{d_{b} }}{2.35} = 255\,\mu{\text{m}}\)

  • temporal: \( \sigma_{t} = \frac{{\tau_{\rm pulse}}}{2.35} = 85\,{\text{fs}} \)

Due to the millisecond time regime of the titanium treatment, the laser power at the subpicosecond pulses was averaged over the processing time. As a result, an averaged intensity I 0 was calculated and used for the modeling. The averaged power was measured by a commercial calorimeter and compared, respectively, synchronized to the modeling data. In order to get the time dependence at a fixed observation point (y = 0), the moving laser beam intensity I mov was defined as

$$ I_{\rm mov} = I_{0} \exp \left( { - \frac{{x^{2} }}{{2\sigma_{d} }}} \right)\sin \left( {\frac{\pi t}{{v_{s} }}} \right) $$
(2)

Equation 2 contains the spatial distribution \( \exp \left( { - \frac{{x^{2} }}{{2\sigma_{d} }}} \right) \) and the perpendicular movement of the laser beam with the scan velocity used described with a sine function \( \sin \left( {\frac{\pi t}{{v_{s} }}} \right). \) Transient welding simulations normally have to be done in three dimensions, in order to describe the problem correctly. In the present case, the scan velocity is much lower than the melt flow velocity; this allows the use of two-dimensional modeling. Table I shows the used beam parameters.

Table I FEL Beam and Scan Parameters
Full size table

Experimental Setup

Titanium sheets (blank, 1-mm thick, >99.98 pct purity) were cut into pieces 15 × 15 mm2 in size. For the laser treatments, the samples were placed in a chamber first evacuated and then filled with nitrogen (purity 99.999 pct) to a pressure of 1.15 atm. The focused beam reached the sample surface through a fused silica window. In order to treat the whole surface of the samples, the chamber was mounted onto a computer-controlled x-y table. A relative velocity v = 24 mm/s in the x direction was used. Figure 2 shows the processing scheme.

Fig. 2
figure 2

Scanning scheme of the nitriding treatment and the moving melt pool at the symmetry axis

Full size image

The experiments have been realized at the FEL user facility. By means of specific optics, the raw beam approximately 6 cm in diameter was redirected to the lens and focused to the used spot size. In addition, a camera was installed for monitoring the treatments. In Figure 3, a snapshot taken during the irradiation is shown. After the treatments, scanning electron microscopy (SEM) was performed with a LEO Supra 35 Gemini (Carl Zeiss SMT AG, Oberkochen, Germany); all images were recorded with a quadral backscattering detector.

Fig. 3
figure 3

Experimental setup consisting of X-Y table, lens, N2 chamber, and N2 supply

Full size image

Free Surface Modeling

Because of the forceful influence of the advection, convection, and conduction effects during the laser treatment, the surface deformation is not negligible. In order to model the surface tracking, the level set method was applied. A function ϕ(x,y,t) was defined over the entire domain, to describe the interface according to the following criteria:

$$ \phi \left( {x,y,t} \right) = \left[ \begin{gathered} > 0.5\quad {\text{nitrogen}} \hfill \\ = 0.5\quad {\text{interface}} \hfill \\ < 0.5\quad {\text{titanium}} \hfill \\ \end{gathered} \right. $$
(3)

The interface movement can be described by a simple partial differential equation, which can be solved numerically at the same time as the Navier–Stokes, heat-transfer, and diffusion equations. Olsson et al.[13,14] used the following the expression:

$$ \frac{\partial \phi }{\partial t} + {\mathbf{u}}\,{\cdot}\,\nabla \phi = \gamma_{L} \nabla\,{\cdot}\,\left( {\varepsilon \left( {\left( {\nabla \phi\,{\cdot}\,{\mathbf{n}}} \right){\mathbf{n}}} \right) - \phi \left( {{\mathbf{1}} - \phi } \right)\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right) $$
(4)

Here, the vector u is the speed function of the surface tracking, which is a result of the Navier–Stokes equation and the normal vectors of the interface n. The term on the right side that describes the interface thickness ε was set to ε > 2 h (3 to 4 mesh elements for improving convergence), in line with the suggestions of some authors.[8,15,16] The term h is the mesh size and γ L is a stabilization parameter that determines the repetition of the reinitialization for each time step. The γ L was set equal to 1, in order to avoid mass loss during the calculation and keep the interface thickness constant. The interface normal vector is defined by

$$ {\mathbf{n}} = \left. {\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right|_{\phi = 0.5} , $$
(5)

which is important in computing the surface curvature κ S , given as

$$ \kappa_{S} = \left. { - \nabla {\mathbf{n}}} \right|_{\phi = 0.5} $$
(6)

and in implementing the surface tension force. A smoothed, continuously differentiable delta function was defined to accommodate the boundary conditions at the interface:

$$ \delta = 6\left| {\nabla \phi } \right|\left| {\phi \left( {1 - \phi } \right)} \right| $$
(7)

As a result, it is possible to transform boundary forces to volumetric ones. Due to the smeared-out interface, the material parameters along the interface were described by Eq. [8]; f corresponds to the different physical properties (density (ρ), viscosity (η), etc.) of titanium and nitrogen.

$$ f = f_{Ti} + \left( {f_{N} - f_{Ti} } \right)\phi $$
(8)

The initial level set function ϕ 0 was set to y − 0.001 = 0, according to the geometry.

Heating and Evaporation

The classical heating of metals during laser irradiation can be described with the normal heat transport equation:

$$ \rho \left( T \right)c_{p} \left( T \right)\frac{\partial T}{\partial t} = \nabla\,{\cdot}\,\left( {\kappa \left( T \right)\nabla T} \right) + Q_{\rm int} \delta - \vec{u}\rho \left( T \right)c_{p} \left( T \right)\nabla T $$
(9)

which contains the source term

$$ \begin{gathered} Q_{\rm int} = \left[ {\alpha_{\rm ext} \left( {1 - R_{s,l} \left( T \right)} \right)I_{\rm mov} \left( {\vec{r},t} \right)} \right] \hfill \\ \underbrace {{ - h_{t} \left( {T - T_{0} } \right) - \sigma_{B} \varepsilon_{B} \left( {T^{4} - T_{0}^{4} } \right) - L_{ev} J_{ev} }}_{{Q_{\rm loss} }} \hfill \\ \end{gathered} $$
(10)

In this equation, the melting behavior, surface temperature, and heat loss Q loss are calculated. The specific heat and the thermal conductivity shown in Figures 4 and 5 were calculated by the data from the National Institute of Standards and Technology.[17] The c p was modified to accommodate the phase transition. Therefore, the latent heats were added as a strong increase in specific heat at the phase-change temperature, shown by the rectangles in Figure 4.

Fig. 4
figure 4

Temperature-dependent specific heat c p and added latent heats of fusion L m and evaporation L ev in the manner of rectangles on the temperature regimes. Data based on Ref. 17

Full size image
Fig. 5
figure 5

Thermal conductivity as a function of temperature[17]

Full size image

The mathematical description of phase changes is a difficulty formally known as the Stefan problem. In our case, there are two free boundaries (the top and bottom of the melt pool) for a parabolic equation. To solve the problem, the smoothed Heaviside function Θ(T,B) was used; B is the width of the temperature region in which Θ(T,B) changes from 0 to 1 and was assumed to be 50 K:

$$ f\left( T \right) = f_{\rm sol} - \left( {f_{\rm sol} + f_{\rm liq} } \right)\,{\cdot}\,\Uptheta \left( {T,B} \right) $$
(11)

Concerning our problem, function 11 was used for the reflectivity R s,l and the mass density ρ(T). For the reflectivity of the solid and liquid phase of titanium, the values were interpolated from the experimental data of Xie.[18] The radiation and convective heat losses to the surroundings were taken into account by the well-known formulations for convective heat transfer and the Stefan–Boltzmann law. The values of the heat-transfer coefficient h t and the emissivity ε are shown in Table II. Additionally, the external absorption parameter α ext was defined to account for heat losses due to the optics, chamber, and soiling and was prescribed equal to 0.32.

Table II Physical Properties of Titanium and Nitrogen Used in Simulations[19–25]
Full size table

The high temperature leads to the evaporation and ablation of titanium in the ambient atmosphere. At the surface, a saturation pressure P S (T S ) originates; this was calculated by the integrated Clausius–Clapyron equation:

$$ P_{S} \left( {T_{S} } \right) = P_{0} \exp \left( {\frac{{L_{ev} \left( {T_{S} - T_{b} } \right)}}{{R_{g} T_{S} T_{b} }}} \right), $$
(12)

where L ev is the latent heat of evaporation, P 0 the reference pressure (1 atm) at the normal boiling point T b , T S the surface temperature, and R g the universal gas constant. In the literature, varying values of parameters are available due to the different compositions of the alloys and other modifications. Consequently, the data of pure titanium (Table II) were taken as far as possible.

The evaporation flux was calculated according to the Langmuir equation:

$$ J_{ev} = \frac{{nP_{S} \left( T \right)}}{{\sqrt {2\pi M_{Ti} R_{gTi} T} }}, $$
(13)

and is usually an order of magnitude higher than the real physical rate at 1 atm pressure. As a result, n was set to be 0.1.[26,27] Furthermore, it is possible to calculate the heat loss at the interface due to evaporation (the mathematical description is shown in Eq. [9] as the last term of Q loss).

Hydrodynamics

For the assembly of the transport equation, the maximum flow velocity in the melt pool has to be calculated empirically[28] as

$$ V_{\max } \approx \left( {\frac{\partial \gamma }{\partial T}\frac{dT}{dy}\frac{{W^{0.5} }}{{0.664\rho^{0.5} \mu_{\rm eff}^{0.5} }}} \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}} $$
(14)

This expression allows for an estimation of the flow motion and the expected surface deformation. In Table III, all used values are shown. As a result, V max was calculated to be approximately 2 m/s, which is on the order of magnitude of such materials-processing techniques.

On the supposition that a melt is an incompressible fluid, the Navier–Stokes equation can be used to describe the fluid motion in the melt pool:

$$ \rho \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} + {\mathbf{u}}\nabla {\mathbf{u}}} \right) = \nabla\,{\cdot}\,\left( { - P_{hyd} {\mathbf{I}} + \eta \left( {\nabla {\mathbf{u}} + \left( {\nabla {\mathbf{u}}} \right)^{T} } \right)} \right) + {\mathbf{F}}_{{{\rm sur}}} + {\mathbf{F}}_{{g}} $$
(15)

containing the equation of continuity:

$$ \nabla\,{\cdot}\,{\mathbf{u}} = 0 $$
(16)

It contains the mass density ρ, the dynamic viscosity η, and the hydrodynamic pressure P hyd. Moreover the velocity field u is divergence free. The last term on the right side describes the buoyancy force F g (Eq. [17]), which was applied in the Boussinesq approximation to take into account the volumetric change due to thermal expansion:

$$ {\mathbf{F}}_{g} = \rho {\mathbf{g}}\beta_{T} \left( {T - T_{L} } \right) $$
(17)

The force F sur at the surface is a superposition of the surface tension force, the Marangoni force and the recoil pressure induced force:

$$ {\mathbf{F}}_{\rm sur} = \left[ {2\sigma \kappa_{S} {\mathbf{n}} - \frac{\partial \sigma }{\partial T}\left( {{\mathbf{I}} - {\mathbf{nn}}} \right)\,{\cdot}\,\nabla T + {\mathbf{n}}\,{\cdot}\,P_{\rm recoil} } \right]\delta , $$
(18)

whereas the acting forces were multiplied by δ to insure that they appear only at the interface. The σ is the surface tension of liquid titanium, κ S is the interface curvature, n is the normal vector of the interface, [(∂σ)/(∂T)] describes the surface tension coefficient, I is the identity matrix, and P recoil corresponds to the recoil pressure, which can be calculated by[30]

$$ P_{\rm recoil} = 0.55\,P_{S} \left( {T_{S} } \right) $$
(19)

The nitrogen mass transfer convectional diffusion equation together with the other transport equations describes the nitrogen concentration c, according to the expression

$$ \frac{{\partial c\left( {x,y,t} \right)}}{\partial t} + \nabla\,{\cdot}\,\left( {D\left( T \right)\nabla c\left( {x,y,t} \right)} \right) = J_{N} \delta - {\mathbf{u}}\,{\cdot}\,\nabla c\left( {x,y,t} \right) $$
(20)

The nitrogen absorption mass flux Δm per surface element S m was calculated by means of comparisons with the experimental results. Therefore, Eq. [21] from Ponticaud et al.,[24] who performed similar investigations, was modified. Due to the smeared-out interface, the boundary flux has to be recalculated as a volumetric reaction rate, which was done by means of Eq. [7] in the manner of the level set approach:

$$ J_{N} = \frac{{d\left( {\frac{\Updelta m}{{S_{m} }}} \right)}}{dt} = j_{0} e^{{\left( { - \frac{{E_{a} }}{RT}} \right)}} $$
(21)

For simplification, an average flux j 0 per surface element was calculated. The temperature dependence was taken into account via the activation energy E a of nitrogen in titanium. Wood and Paasche[31] found a formulation for the temperature-dependent diffusion coefficient during their studies of the laser irradiation of titanium:

$$ D\left( T \right) \approx 0.12\,{\cdot}\,\exp \left[ {\frac{ - 45200}{1.98\,{\cdot}\,T}} \right], $$
(22)

which represents a typical Arrhenius behavior (values are in cm2/s). Dimensionless numbers are used in fluid dynamics to describe comparable physical problems and to represent specific information such as flow behavior and acting forces. Table IV summarizes all dimensionless numbers used in our simulations, including their physical background. As a result, it is necessary to define the characteristic length L, which is set generally to be the half width of the melt pool.[32]

Table III Physical Properties of Titanium Used for Approximation[23,29]
Full size table
Table IV Dimensionless Numbers and Their Physical Meaning of Ratios
Full size table

Geometry and Boundaries

Modeling of such processes generally requires simplifications and assumptions. From the outset, one must utilize the radial symmetry of the melt pool and compute only one side. An advantage of the level set method is the formulation of volumetric boundary conditions. As a result, only boundaries outside the interface have to be declared mathematically. The symmetry axes were set to slip conditions according Figure 6. At the solid boundaries of the model, the velocity was set to be zero (no slip). No-slip conditions at the solid-liquid interface were obtained by means of a viscosity jump at the melting temperature T L . On the gaseous side, neutral flow conditions were employed. Figure 6 shows the used triangular mesh of Lagrangian elements. It contains 6153 elements with 3135 nodes. This leads to degrees of freedom of 46,671.

Fig. 6
figure 6

Geometry, boundary conditions, and mesh of the simulation

Full size image

The inner boundaries a, b, and c of the used geometry were set to be continuous for the heat and diffusion equation. In this case of heat transfer and diffusion, the elements were linear. All other boundaries outside were assumed to be isolated at the solid and neutral at the gaseous side. The Navier–Stokes and the level set function were solved by means of quadratic elements (P 2 P 1). The Pardiso direct solver[33] was used to compute the transient and two-dimensional analyses. Time stepping was set to be free (solver controlled).

Results

Nitrified Tracks

After irradiation of the titanium in nitrogen ambient, golden gleaming tracks remain along the treated path. During the irradiation, the nitrogen reacts with the molten titanium and forms titanium nitride phases. The top view of the solidified track in Figure 7 reveals a higher roughness than the untreated titanium. The increase in roughness is a result of the Marangoni convection and pressure forces during the treatment.

Fig. 7
figure 7

SEM top view of a solidified track

Full size image

Humps and melt ejection were not observed and, further, the periodical structure is a result of the equilibrium of the surface acting forces. Short-wavelength structures could also be observed. Due to the oscillations on the liquid titanium, such modifications are developed. They are formally known as Rayleigh–Taylor instabilities.

Modeling Results

From the FEM calculations, many details of the processing were obtained. The fluid flow, local heating, and mass transport were described; through these descriptions, information was uncovered about the physical processes that took place during the laser treatments. The time-dependent development of a track during irradiation is illustrated in Figure 8, which shows the temperature distribution (color scale), the flow direction of the melt (indicated by arrows), and the melt pool shape (surrounded by the black line) in cross-sectional view. The t = 0 corresponds to the time step at which the surface temperature exceeds the melting point of titanium and the liquid state is generated at the center of the tracks. The duration of liquefied titanium at the center of the tracks was calculated to be 18 ms. The following investigations and results offer insight into the nitriding physics and the consequences for the synthesized TiN coatings.

Fig. 8
figure 8

Development of the melt pool shape and temperature distribution

Full size image

The Prandtl number (Pr) for the model system was 0.11; it describes the flow properties of a liquid. The Prandtl number of liquid Ti indicates an intense flow behavior.[32] As expected, a strong convectional flow that results from the Marangoni force occurs, as does surface deformation. Due to the supplemental convective heat transfer, the aspect ratio (the ratio of height to width) of the melt pool is very low. For the selected treatment parameters (laser intensity), the temperature did not attain the boiling point. As a consequence, keyhole formation and evaporation could be avoided or minimized, which is a main requirement for cladding or alloying at laser material processing. The simulated maximum velocity of liquid titanium is shown in Figure 9. As a result of the strong temperature gradients, that flow velocity increases quickly to its maximum value of approximately 1 m/s. The continuous decrease that follows depends on the pool volume and acting forces. However, the accuracy of this value is not very good because of the strong dependencies on the viscosity and the acting forces and their implementation in the model (boundary-to-volume force).

Fig. 9
figure 9

Maximum melt flow velocity and corresponding Reynolds number, at different times

Full size image

In order to get comparable data for other treatments, the process was described by dimensionless numbers according to Table IV. The development of the Reynolds number (Re), the most important one, is also shown in Figure 9 for the whole process; it exceeds a value of 500. Relying on the data, it is possible to get information about the flow regime. There are no data available for critical Reynolds numbers in melt pools in order to derive laminar or turbulent flow, but several approaches to solving the problem are available. Atthey et al.[34] proposed a full turbulent flow at a Re of approximately 600. Other investigations were performed by Chakraborty et al.[35,36] for similar treatments. A comparison with their data proposed a turbulent flow for the presented treatments. Lately, the flow was assumed to be laminar as a first approximation. The computed results offer insight into the studied physical process.

A very important characteristic number is the Peclet number (Pe), which offers information about the heat-transfer mechanism. High values match a dominating convective transport. This behavior is very important for the quality of the TiN tracks, particularly for the solidification. The results in Figure 10 were calculated as the integrated average of the heat transport process in the whole liquid pool. As represented, the convective transport is approximately 10 times higher than the conductive one in the melt pool. This is a main primary reason for the low aspect ratio and a melting depth of approximately 200 microns. The heat transport is stronger in the direction parallel to the surface. The intensity of the Marangoni flow is described by the Marangoni number (Ma) shown in Figure 11. It is approximately 5000 at the assumed flow regime. This is a very typical value for laser welding.

Fig. 10
figure 10

Average Peclet number development of the whole melt pool during the treatment

Full size image
Fig. 11
figure 11

Marangoni number for the whole process

Full size image

As a consequence of the observed surface deformation, it is important to get quantitative data about the acting forces and their relationships, in order to understand and control the processing. The Weber (We) and capillary (Ca) numbers shown in Figure 12 describe the ratios of the inertial and Marangoni forces to the viscous force and the surface tension force, respectively. A Weber number close to unity satisfies strong flow. The inertial forces are similar to the surface tension forces in intensity. In relation to the surface deformation, the Ca is the main determining parameter. For low values close to zero, the resulting melt pool shape can be assumed to be flat; if Ca increases, however, the deformation must not be neglected. The acting forces become very strong and countervail the surface tension. If Ca increases to values up to 1, melt ejection is possible. Due to the observed track profiles and comparison with the simulation, a value of approximately 0.1 seems to be in the right order of magnitude. The knowledge of We and Ca allows for control of the nitriding process and optimization of the surface quality.

Fig. 12
figure 12

Weber and capillary number development

Full size image

Figure 13 represents the characteristics of the acting forces. The values were calculated as averages over the whole liquid surface. The primary observation is that the surface tension force is always stronger than the other ones. That is the primary reason that neither melt ejection nor droplets could be observed. This behavior mainly determines the track properties and, at the very least, the coating quality. It is very important for the nitriding process that the pressure-induced recoil force is lower than the surface tension force, because values of F recoil that are too high would induce a keyhole. This drilling effect should be avoided in order to get flat laser-nitrided tracks. The control of the process is possible by keeping the surface temperature below the boiling point by means of moderate laser intensity. On the other hand, energies that are too low result in a disadvantage for the nitride synthesis. Because of evaporation, plasma development occurs; this leads to nitrogen dissociation on top of the melt pool. This nitrogen activation process increases significantly the nitrogen adsorption and the absorption diffusion,[4] which leads to an effective coating synthesis. This conflict has to be optimized in relation to the whole process. Concerning the buoyancy force, the simulations show a negligible influence on the flow regime and the pool shape. The describing parameter is the Grashoff number Gr. The Gr numbers were calculated to be approximately 0.05, which is 5 orders of magnitude lower than Ma. In a physical sense, the calculation verifies the dominating influence of the Marangoni effect.

Fig. 13
figure 13

Absolute values of the three acting boundary forces expressed as volumetric forces along the whole liquid surface

Full size image

The energy balance at the surface is shown in Figure 14. This describes the energy terms during the treatment. In the first few milliseconds of the interaction time, the heat loss is marginal; after exceeding the melting point and reaching higher temperatures, however, the energy loss, mainly due to evaporation, becomes important. Radiation effects according to the Stefan–Boltzmann law can be neglected. Moreover, the convective heat transfer due to the gas motion on top on the surface was described and was calculated to have a negligible influence. As expected, the evaporation heat loss Q vap calculated by means of the Langmuir equation becomes significant. For high temperatures (close to the boiling point), it becomes the dominant acting process. In relation to the synthesis of TiN coatings, it is important to get an optimized ratio between the heat loss and the absorbed energy. To fulfill this condition, the surface temperature should be close to the boiling point during the irradiation.

Fig. 14
figure 14

Energy balance on top on the titanium surface

Full size image

Nitrogen Transport and Comparison

In order to obtain more details about the nitrogen incorporation, the mass transport equation was coupled with the complete equation system. Due to the strong convective flow, the nitrogen transport is a combination of diffusion and convection. The nitrogen absorption at the interface would normally be derived by Sievert’s law. However, in the present case, the flux was calculated as an average flux over the whole liquid surface by comparison with the experimental results and the temperature-dependent activation energy E a of nitrogen in titanium. As a result, the j 0 in Eq. [21] was calculated to be 11.2·106 mol/m2 s.

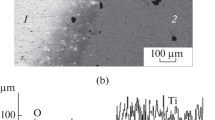
The ratio of the convective to diffusive mass transport is described by the Schmidt number (Sc); this was calculated to be approximately 200 close to the surface. As a disadvantage of the mathematical model (smeared-out interface), the diffusion behavior was unable to be investigated. The mesh size was greater than the expected diffusion length. Figure 15 represents the calculated nitrogen distribution in the melt pool at different time steps. Additionally, the flow induced by the Marangoni effect is indicated with arrows. The results show a homogenous distribution due to the laminar flow and the unchanged physical properties of the liquid titanium in solution with nitrogen. In a comparison of the cross-sectional micrograph in Figure 16 with similar investigations in the literature,[37,38] some differences are shown, especially in the homogeneity.

Fig. 15
figure 15

Simulated nitrogen distribution in the melt pool (scale: white = 0 and black = 50 (atm pct)). Arrows indicate the flow direction

Full size image
Fig. 16
figure 16

Comparison of the simulated melt pool shape with a cross-sectional micrograph

Full size image

Due to the increase in the nitrogen content in the melt, solidification occurs at the track, in particular, at the edges. Close to the surface, stoichiometric TiN was observed (the black region in Figure 16). Figure 17 represents the growth of TiN dendrites at the tracks; these are top down in direction. Because of the melting point of 3220 K, the TiN system solidified early above the liquid titanium and the flow is disturbed. This leads to a decrease in nitrogen content in the deeper pool regions, in contrast to the simulations. The observed experimental result is shown in Figure 16 and corresponds to TiN x or N dissolved in pure titanium. Due to the disturbed flow, the whole process gets very complex and turbulent.

Fig. 17
figure 17

Dendritic solidified titanium nitride at the track edge

Full size image

Conclusions

The current work presents investigations regarding the FEL nitriding of titanium in an ambient nitrogen atmosphere. A finite element method simulation was performed in order to describe the processes taking place, in particular, the melting and flow behavior, i.e., the nitrogen transport. The surface deformation that resulted from strong convection was taken into account by means of the level set method for gas-liquid interfaces. As a result, the flow motion and surface deformation were calculated and at least described with dimensionless numbers. The Reynolds number Re was calculated to be approximately 500 during the treatments. As a result of the calculations, the dominant heat transport process was determined to be convection, which is verified by an average Peclet number Pe in the melt pool of approximately 10. The melt flow velocity induced by the Marangoni force has been calculated to be approximately 1 m/s. This strong flow is also the governing process of the nitrogen transport. It was shown that the Schmidt number at the surface can reach values up to 200. Next, the simulations were compared with cross-sectional micrographs. The calculated melt pool shape correlates with the experimental results, but the nitrogen distribution computed by means of the model still has some differences, in particular, at the pool bottom. The micrographs show stoichiometric titanium nitride TiN close to the surface (black region) and understoichiometric TiN x in the deeper pool area. Because of changes in the viscosity due to the TiN formation, particularly at the edges, the flow is disturbed. It is necessary to modify the viscosity with nitrogen content dependency in further investigations and simulations.

In relation to the laser gas alloying process and other cladding techniques such as plasma or gas nitriding, some criteria emerged during the investigations. Concerning the technical surfaces, there is a discrepancy between the surface quality and the film thickness. For deeper nitriding, it is necessary to increase the melting depth and the convectional flow, which leads to efficient nitrogen transport in deeper regions. On the other hand, this requires higher energy densities, which lead to large surface deformation because of strong capillary forces and a decrease in quality (roughness).