Skip to main content
SpringerLink
Log in

Investigation of Heat Transfer Augmentation between the Ribbed Plates via Taguchi Approach and Computational Fluid Dynamics

  • Published:
Journal of Thermal Science Aims and scope Submit manuscript

Abstract

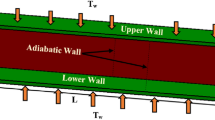
Heat transfer and turbulent flow characteristics between the ribbed plates have been numerically studied in the present paper. The ribs with the rectangular cross-section have been placed on the top and the bottom plates of the duct, symmetrically. It is assumed that the fluid at 300 K has entered the system while the walls kept at 400 K. All numerical analyses have been performed by k-ω Shear Stress Transport (SST) turbulence model for Re = 10000, 15000 and 20000. For the fixed rib width, the dimensionless height and the dimensionless spacing have been respectively varied as 0.1 ≤ h′ ≤ 0.3 and 0.5 ≤ S′ ≤ 1, and the results have been compared with the ones of the smooth plate. Even though there are twenty-seven cases obtained as a result of parametric combinations, the number of various cases has been reduced from twenty-seven to only nine different variations by applying the Taguchi method. Furthermore, the effects of all the considered parameters on the heat transfer and flow characteristics have been determined in terms of the influence degree. The optimum parameters for Nusselt number and pressure loss have been ascertained individually. What is more, the almost exact values for Nusselt number and pressure loss have also been attained by the confirmation test having an error percentage of 6%. The most dominant factor has been determined as the rib height due to its effect on both heat transfer and flow characteristics. Similarly, with respect to the numerical results, increasing the rib height, the rib spacing and Reynolds number has separately increased Nusselt number. Nevertheless, symmetrical flow structure has been disturbed as a result of ascending the rib height as clearly seen for h′ = 0.3 from the charts. In the meantime, pressure loss has been augmented owing to the increment of the geometrical parameters and also Reynolds number. h′ = 0.1 with S′ = 0.5 at Re = 10000, h′ = 0.2 with S′ = 0.5 at Re = 15000 and h′ = 0.1 with S′ = 0.75 at Re = 15000 can be suggested for the heat transfer enhancement since the pressure loss of the system is tolerated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Kakac S., Transient forced convection heat transfer in a channel. Hat and Mass Transfer, 1968, 1(3): 169–176.

    Google Scholar 

  2. Özsunar A., Kare kesitli yatay bir kanalda laminer karışık konveksiyon akışın incelenmesi. Teknoloji, 2001, 1–2: 149–158. (in Turkish)

    Google Scholar 

  3. Shibani A.A., Ozisik M.N., A solution to heat transfer in turbulent flow between parallel plates. International Journal of Heat and Mass Transfer, 1977, 20(5): 565–573.

    Article  ADS  Google Scholar 

  4. Aksoy Y., Effects of couple stresses on the heat transfer and entropy generation rates for a flow between parallel plates with constant heat flux. International Journal of Thermal Sciences, 2016, 107: 1–12.

    Article  Google Scholar 

  5. Bejan A., Sciubba E., The optimal spacing of parallel plates cooled by forced convection. International Journal of Heat and Mass Transfer, 1992, 35(12): 3259–3264.

    Article  Google Scholar 

  6. Dean R.B., Reynolds number dependence of skin friction and other bulk flow variables in two-dimensional rectangular duct flow. Journal of Fluids Engineering, 1978, 100(2): 215–223.

    Article  Google Scholar 

  7. Sakakibara M., Analysis of heat transfer in the entrance region with fully developed turbulent flow between parallel plates-the case of uniform wall heat flux. Memoirs of the Faculty of Engineering Fukui University, 1982, 30(2): 107–120.

    Google Scholar 

  8. Weigand B., Schwartzkopff T., Sommer T.P., A numerical investigation of the heat transfer in a parallel plate channel with piecewise constant wall temperature boundary conditions. Journal of Heat Transfer, 2002, 124(4): 626–634.

    Article  Google Scholar 

  9. Osborne D.G., Incropera F.P., Experimental study of mixed convection heat transfer for transitional and turbulent flow between horizontal, parallel plates. International journal of heat and mass transfer, 1985, 28(7): 1337–1344.

    Article  Google Scholar 

  10. Silin N., Masson V.P., Marino R., Heat transfer in a short parallel-plate channel in the transition regime. Experimental Heat Transfer, 2012, 25(1): 12–29.

    Article  ADS  Google Scholar 

  11. Turgut O., Onur N., An experimental and three-dimensional numerical study of natural convection heat transfer between two horizontal parallel plates. International Communications in Heat and Mass Transfer, 2007, 34(5): 644–652.

    Article  Google Scholar 

  12. Ozisik M.N., Cotta R.M., Kim W.S., Heat transfer in turbulent forced convection between parallel - plates. The Canadian Journal of Chemical Engineering, 1989, 67(5): 771–776.

    Article  Google Scholar 

  13. Yang H., Zhu Z., Gilleard J., Numerical simulation of thermal fluid instability between two horizontal parallel plates. International Journal of Heat and Mass Transfer, 2001, 44(8): 1485–1493.

    Article  MATH  Google Scholar 

  14. Desrues T., Marty P., Fourmigué J.F., Numerical prediction of heat transfer and pressure drop in three-dimensional channels with alternated opposed ribs. Applied Thermal Engineering, 2012, 45–46: 52–63.

    Article  Google Scholar 

  15. Liu H., Wang J., Numerical investigation on synthetical performances of fluid flow and heat transfer of semiattached rib-channels. International Journal of Heat and Mass Transfer, 2011, 54(1–3): 575–583.

    Article  MATH  Google Scholar 

  16. Marocco L., Franco A., Direct Numerical Simulation and RANS comparison of turbulent convective heat transfer in a staggered ribbed channel with high blockage. Journal of Heat Transfer, 2017, 139(2): 021701–021701–7.

    Article  Google Scholar 

  17. Mayle R.E., Pressure loss and heat transfer in channels roughened on two opposed walls. Journal of Turbomachinery, 1991, 113(1): 60–66.

    Article  Google Scholar 

  18. Webb B.W., Ramadhyani S., Conjugate heat transfer in a channel with staggered ribs. International Journal of Heat and Mass Transfer, 1985, 28(9): 1679–1687.

    Article  Google Scholar 

  19. Wongcharee K., Changcharoen W., Eiamsa-ard S., Numerical investigation of flow friction and heat transfer in a channel with various shaped ribs mounted on two opposite ribbed walls. International Journal of Chemical Reactor Engineering, 2011, 9(1): A26 1–22.

    Article  Google Scholar 

  20. Xie G., Li S., Zhang W., Sundén B., Computational Fluid Dynamics modeling flow field and side-wall heat transfer in rectangular rib-roughened passages. Journal of Energy Resources Technology, 2013. 135(4): 042001–042001–8.

    Article  Google Scholar 

  21. Hwang J.J., Liou T.M., Effect of permeable ribs on heat transfer and friction in a rectangular channel. Journal of Turbomachinery, 1995, 117(2): 265–271.

    Article  ADS  Google Scholar 

  22. Lopez J.R., Anand N.K., Fletcher L.S., Heat transfer in a three-dimensional channel with baffles. Numerical Heat Transfer, Part A: Applications, 1996, 30(2): 189–205.

    Article  ADS  Google Scholar 

  23. Tafti D.K., Evaluating the role of subgrid stress modeling in a ribbed duct for the internal cooling of turbine blades. International Journal of Heat and Fluid Flow, 2005, 26(1): 92–104.

    Article  Google Scholar 

  24. Tokgoz N., Aksoy M.M., Sahin B., Investigation of flow characteristics and heat transfer enhancement of corrugated duct geometries. Applied Thermal Engineering, 2017, 118: 518–530.

    Article  Google Scholar 

  25. Promvonge P., Thianpong C., Thermal performance assessment of turbulent channel flows over different shaped ribs. International Communications in Heat and Mass Transfer, 2008, 35(10): 1327–1334.

    Article  Google Scholar 

  26. Skullong S., Thianpong C., Promvonge P., Effects of rib size and arrangement on forced convective heat transfer in a solar air heater channel. Heat and Mass Transfer, 2015, 51(10): 1475–1485.

    Article  ADS  Google Scholar 

  27. Vanaki S.M., Mohammed H.A., Numerical study of nanofluid forced convection flow in channels using different shaped transverse ribs. International Communications in Heat and Mass Transfer, 2015, 67: 176–188.

    Article  Google Scholar 

  28. Yang W., Xue S., He Y., Li W., Experimental study on the heat transfer characteristics of high blockage ribs channel. Experimental Thermal and Fluid Science, 2017, 83: 248–259.

    Article  Google Scholar 

  29. Shyam S., Datta A., Das A.K., Numerical analysis of fluid flow and heat transfer of flow between parallel plates having rectangular shape micromixer. Journal of Thermal Science and Engineering Applications, 2017, 10(1): 011003–011003–8.

    Google Scholar 

  30. Ma C., Ji Y., Ge B., Zang S., Chen H., Comparative study of convective heat transfer performance of steam and air flow in rib roughened channels. Journal of Thermal Science, 2018, 27(2): 184–194.

    Article  ADS  Google Scholar 

  31. Szwaba R., Kaczynski P., Telega J., Doerffer P., Influence of internal channel geometry of gas turbine blade on flow structure and heat transfer. Journal of Thermal Science, 2017, 26(6): 514–522.

    Article  ADS  Google Scholar 

  32. Kilicaslan I., Sarac H.I., Enhancement of heat transfer in compact heat exchanger by different type of rib with holographic interferometry. Experimental Thermal and Fluid Science, 1998, 17(4): 339–346.

    Article  Google Scholar 

  33. Aslan E., Taymaz I., Islamoglu Y., Finite volume simulation for convective heat transfer in wavy channels. Heat and Mass Transfer, 2016, 52(3): 483–497.

    Article  ADS  Google Scholar 

  34. Pehlivan H., Taymaz I., Islamoglu Y., Experimental study of forced convective heat transfer in a different arranged corrugated channel. International Communications in Heat and Mass Transfer, 2013, 46: 106–111.

    Article  Google Scholar 

  35. Yemenici O., Umur H., Experimental aspects of heat transfer enhancement over various flow surfaces. Heat Transfer Engineering, 2016, 37(5): 435–442.

    Article  ADS  Google Scholar 

  36. Sripattanapipat S., Promvonge P., Numerical analysis of laminar heat transfer in a channel with diamond-shaped baffles. International Communications in Heat and Mass Transfer, 2009, 36(1): 32–38.

    Article  Google Scholar 

  37. Jaswal I., Ames F.E., Heat transfer and pressure drop measurements in constant and converging section pin and diamond pedestal arrays. Journal of Thermal Science and Engineering Applications, 2009, 1(1): 011006–011006–7.

    Article  Google Scholar 

  38. Ahmed M.A., Yusoff M.Z., Shuaib N.H., Effects of geometrical parameters on the flow and heat transfer characteristics in trapezoidal-corrugated channel using nanofluid. International Communications in Heat and Mass Transfer, 2013, 42: 69–74.

    Article  Google Scholar 

  39. Taguchi G., System of experimental design: engineering methods to optimize quality and minimize costs. 1987, UNIPUB/Kraus International Publications.

    Google Scholar 

  40. Bagci M., Imrek H., Application of Taguchi method on optimization of testing parameters for erosion of glass fiber reinforced epoxy composite materials. Materials and Design, 2013, 46: 706–712.

    Article  Google Scholar 

  41. Bilen K., Yapici S., Celik C., A Taguchi approach for investigation of heat transfer from a surface equipped with rectangular blocks. Energy Conversion and Management, 2001, 42(8): 951–961.

    Article  Google Scholar 

  42. Turgut E., Cakmak G., Yildiz C., Optimization of the concentric heat exchanger with injector tabulators by Taguchi method. Energy Conversion and Management, 2012, 53(1): 268–275.

    Article  Google Scholar 

  43. Tinkir M., Dilmec M., Turkoz M., Halkaci H.S., Investigation of the effect of hydromechanical deep drawing process parameters on formability of AA5754 sheets metals by using neuro-fuzzy forecasting approach. Journal of Intelligent and Fuzzy Systems: Applications in Engineering and Technology, 2015, 28(2): 647–659.

    Article  Google Scholar 

  44. Karbalaei M.J., Nejat A., Panahi M.S., Heat transfer improvement in automotive brake disks via shape optimization of cooling vanes using improved TPSO algorithm coupled with Artificial Neural Network. Journal of Thermal Science and Engineering Applications, 2017, 10(1): 011013–011013–14.

    Google Scholar 

  45. Aly W.I.A., Computational Fluid Dynamics and optimization of flow and heat transfer in coiled tube-in-tube heat exchangers under turbulent flow conditions. Journal of Thermal Science and Engineering Applications, 2014, 6(3): 031001–031001–10.

    Article  Google Scholar 

  46. Marucho M.D., Campo A., Cheikh N.B., Time estimate for the incipient surface melting of regular-shaped metals receiving uniform heat flux inside a metal melting furnace. Journal of Thermal Science and Engineering Applications, 2016, 8(2): 021002–021002–6.

    Article  Google Scholar 

  47. Cengel Y.A., Cimbala J.M., Akişkanlar Mekaniği: Temelleri ve Uygulamalari. 2008, Güven Bilimsel. (in Turkish)

    Google Scholar 

  48. Matsubara K., Ohta H., Miura T., Entrance region heat transfer in a channel with a ribbed wall. Journal of Heat Transfer, 2016, 138(12): 122001–122001–7.

    Article  Google Scholar 

  49. Anonymous, ANSYS-Fluent 12.0 Theory Guide. 2009, ANSYS Inc., 816.

  50. Phadke M.S., Quality engineering using robust design. 1989, Englewood Cliffs, New Jersey: PTR Prentice-Hall Inc.

    Google Scholar 

  51. Han J.C., Heat transfer and friction characteristics in rectangular channels with rib turbulators. Journal of Heat Transfer, 1988, 110(2): 321–328.

    Article  Google Scholar 

  52. Lorenz S., Mukomilow D., Leiner W., Distribution of the heat transfer coefficient in a channel with periodic transverse grooves. Experimental Thermal and Fluid Science, 1995, 11(3): 234–242.

    Article  Google Scholar 

  53. Watanabe K., Takahashi T., LES simulation and experimental measurement of fully developed ribbed channel flow and heat transfer. in ASME Turbo Expo 2002: Power for Land, Sea, and Air. Amsterdam, The Netherlands. 2002, GT2002-30203: 411–417.

    Google Scholar 

Download references

Acknowledgments

All authors would like to express their appreciation to 2015-OYP-007 of Selcuk University Academic Staff Training Program (OYP).

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Faculty of Engineering and Natural Sciences, Konya Technical University, Konya, 42075, Turkey

    Ilker Goktepeli, Ulas Atmaca & Abdullah Cakan

Authors
  1. Ilker Goktepeli
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ulas Atmaca
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Abdullah Cakan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ilker Goktepeli.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Goktepeli, I., Atmaca, U. & Cakan, A. Investigation of Heat Transfer Augmentation between the Ribbed Plates via Taguchi Approach and Computational Fluid Dynamics. J. Therm. Sci. 29, 647–666 (2020). https://doi.org/10.1007/s11630-019-1155-z

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11630-019-1155-z

Keywords

Search

Navigation