Simulation of a shock tube with a small exit nozzle

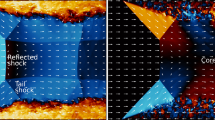
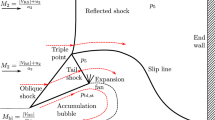
Abstract

Shock tubes are frequently used to rapidly heat up reaction mixtures to study chemical reaction mechanisms and kinetics in the field of combustion chemistry [1]. In the present work, the flow field inside a shock tube with a small nozzle in the end plate has been investigated to support the analysis of reacting chemical mixtures with an attached mass spectrometer and to clarify whether the usual assumptions for the flow field and the related thermodynamics are fulfilled. In the present work, the details of the flow physics inside the tube and the flow out of the nozzle in the end plate have been investigated. Due to the large differences in the typical length scales and the large pressure ratios of this special device, a very strong numerical stiffness prevails during the simulation process. Second-order ROE numerical schemes have been employed to simulate the flow field inside the shock tube. The simulations were performed with the commercial code ANSYS Fluent [2]. Axial-symmetric boundary conditions are employed to reduce the consumption of CPU time. A density-based transient scheme has been used and validated in terms of accuracy and efficiency. The simulation results for pressure and density are compared with analytical solutions. Numerical results show that a density-based numerical scheme performs better when dealing with shock-tube problems [5]. The flow field near the nozzle is studied in detail, and the effects of the nozzle to pressure and temperature variations inside the tube are investigated. The results show that this special shock-tube setup can be used to study high-temperature gas-phase chemical reactions with reasonable accuracy.