A probabilistic tool for multi-hazard risk analysis using a bow-tie approach: application to environmental risk assessments for geo-resource development projects

Abstract

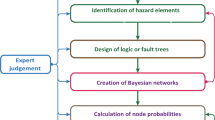
In this paper, we present a methodology and a computational tool for performing environmental risk assessments for geo-resource development projects. The main scope is to implement a quantitative model for performing highly specialised multi-hazard risk assessments in which risk pathway scenarios are structured using a bow-tie approach, which implies the integrated analysis of fault trees and event trees. Such a model needs to be defined in the interface between a natural/built/social environment and a geo-resource development activity perturbing it. The methodology presented in this paper is suitable for performing dynamic environmental risk assessments using state-of-the-art knowledge and is characterised by: (1) the bow-tie structure coupled with a wide range of probabilistic models flexible enough to consider different typologies of phenomena; (2) the Bayesian implementation for data assimilation; (3) the handling and propagation of modelling uncertainties; and (4) the possibility of integrating data derived form integrated assessment modelling. Beyond the stochastic models usually considered for reliability analyses, we discuss the integration of physical reliability models particularly relevant for considering the effects of external hazards and/or the interactions between industrial activities and the response of the environment in which such activities are performed. The performance of the proposed methodology is illustrated using a case study focused on the assessment of groundwater pollution scenarios associated with the management of flowback fluids after hydraulically fracturing a geologic formation. The results of the multi-hazard risk assessment are summarised using a risk matrix in which the quantitative assessments (likelihood and consequences) of the different risk pathway scenarios considered in the analysis can be compared. Finally, we introduce an open-access, web-based, service called MERGER, which constitutes a functional tool able to quantitatively evaluate risk scenarios using a bow-tie approach.

Appendices

Appendix 1: Basic probabilistic models for setting BE in fault trees and nodes in event trees

Events characterised by the homogeneous Poisson process

The inference problem in this case is to estimate the rate of event occurrence ($\lambda$) per time unit. A constant failure rate implies that failures are generated by a Poisson process; therefore, the likelihood function for this evidence can be set using the Poisson distribution:

$$\begin{aligned} p\{r\,{\text{failures}\,\text{in}}\,[0,t]|\lambda \} = \frac{(\lambda t)^r}{r!}e^{-\lambda t} \end{aligned}$$

(5)

A prior distribution for $\lambda$ can be developed from other generic data (as, e.g. data from similar cases or components, or from expert opinion elicitation). Because of the simplicity in calculations, we adopt a conjugate prior for the $\lambda$ parameter, which in this case is the Gamma distribution:

$$\begin{aligned} \pi _0(\lambda ) = \frac{\beta ^\alpha \lambda ^{\alpha -1}}{\varGamma (\alpha )} e^{-\beta \lambda } \end{aligned}$$

(6)

where $\alpha$ and $\beta$ are the parameters characterising this distribution. Usually, the prior state of knowledge can be defined using the actual analyst’s knowledge of a mean value, $E(\lambda )$, as a best value, and a standard deviation, SD($\lambda$), as an uncertainty range. In such a case, the $\alpha$ and $\beta$ parameters of the Gamma prior distribution can be set by solving:

$$\begin{aligned} \left\{ \begin{array}{ll} &{}E(\lambda ) =\frac{\alpha }{\beta }\\ &{}{\mathrm{SD}}(\lambda ) = \frac{\sqrt{\alpha }}{\beta}. \\ \end{array} \right. \end{aligned}$$

(7)

The Posterior distribution, $\pi (\lambda )$, for the Poisson-Gamma conjugate pair is the Gamma distribution:

$$\begin{aligned} \pi _1(\lambda |E) = \frac{\beta '^{\alpha '} \lambda ^{\alpha ' -1}}{\varGamma (\alpha ')} e^{-\beta ' \lambda } \end{aligned}$$

(8)

where

$$\begin{aligned} \alpha ' = \alpha +r \quad \hbox { and }\quad \beta ' = \beta +t \end{aligned}$$

(9)

Once the posterior distribution $\pi _1(\lambda |E)$ has been obtained, $\lambda$ samples are drawn from that posterior distribution and used to calculate the probability of at least one event occurring in a determined period of time $\Delta t$ of interest:

$$\begin{aligned} {\mathrm{Pr}}(r>0, \Delta t) = 1 - e^{-(\lambda \Delta t)}. \end{aligned}$$

(10)

Events characterised by the binomial model

The binomial distribution can be used to model processes whose evidence is given by a number of event occurrences out of a number of trials. Using this model, the likelihood function is the conditional probability of observing r events (e.g. failures, successes, etc.) in n trials, given $\phi$ (i.e. the probability of the event’s occurrence):

$$\begin{aligned} p\{r\,{\mathrm{failures}\,\mathrm{in }}\,n\,{\mathrm{trials}} | \phi \} = \frac{n!}{r! (n-r)!} \phi ^r (1-\phi )^{n-r} \end{aligned}$$

(11)

The conjugate Prior for the binomial distribution is the beta distribution, which has the form:

$$\begin{aligned} \pi _0(\phi ) = \frac{\varGamma (\alpha + \beta )}{\varGamma (\alpha ) \varGamma (\beta )} \phi ^{\alpha - 1} (1-\phi )^{\beta -1} \end{aligned}$$

(12)

where $\alpha$ and $\beta$ are the parameters characterising the beta distribution. To set the model parameters of the prior distribution, the analyst usually can have an average value as the best estimate of the $\phi$ parameter and an interval representing a (prior) uncertainty regarding $\phi$. To set the $\alpha$ and $\beta$ parameters of the beta prior distribution we adopt a simple model in which the analyst set (a) the prior state of knowledge by defining a mean value as the best estimate of the parameter, and (b) to set an uncertainty order of magnitude, the analyst defines the so-called equivalent sample size, $\varLambda , (\varLambda >0)$, which is a number representing the quantity of data that the analyst expects to have in order to modify his prior beliefs regarding the parameter (Marzocchi et al. 2008). It means that the larger $\varLambda$, the more confident the analyst is about his prior state of knowledge. For example, setting $\varLambda =1$ the analyst is expressing a maximum uncertainty condition, implying that just one single observation can substantially modify the prior state of knowledge.

Once these two parameters have been defined, the parameters of the beta prior distribution can be set using the following equations (Marzocchi et al. 2008):

$$\begin{aligned} \alpha = \theta (\varLambda +1)\quad \hbox { and }\quad \beta = \varLambda +1 - \alpha . \end{aligned}$$

(13)

The posterior distribution, $\pi _1(\phi )$, for the binomial-beta conjugate pair is the beta distribution:

$$\begin{aligned} \pi _1(\phi |E) = \frac{\varGamma (\alpha ' + \beta ')}{\varGamma (\alpha ') \varGamma (\beta ')} \phi ^{\alpha ' - 1} (1-\phi )^{\beta ' -1} \end{aligned}$$

(14)

where

$$\begin{aligned} \alpha ' = \alpha +r\quad \hbox { and } \quad \beta ' = \beta +n-t. \end{aligned}$$

(15)

Events characterised by the Weibull model

The Weibull distribution, with parameters $\lambda >0$ and $k>0$ is defined for positive real numbers with Probability density function (e.g. Leemis 2009):

$$\begin{aligned} f(t) = \frac{k}{\lambda } \left( \frac{t}{\lambda } \right) ^{k-1}, \quad {\mathrm{for }}\,t \ge 0 \end{aligned}$$

(16)

where $k>0$ and $\lambda > 0$ are the shape and scale parameters, respectively. k determines the time-dependent behaviour of the hazard rate (with $k<1$, h decreases with time; with $k=1$, h is constant with time, and for $k>1$, h increases with time (i.e. as in an ageing or wearing process). Regarding the methods for determining the model parameter values, the maximum likelihood is the method most widely used (e.g. Leemis 2009).

For a history-dependent point process, the conditional probability that an event happens in a time interval $(x, x, +\Delta t)$, given an interval of $x = (\tau - \tau _{\mathrm{L}})$ years since the occurrence of the previous event (with $\tau$ the current time of the assessment, and $\tau _{\mathrm{L}}$ the time form the last event) can be calculated as follows (see, e.g. Garcia-Aristizabal et al. 2012):

$$\begin{aligned} Pr(x, x+\Delta t) = \frac{\int _x^{x+\Delta t} f(s) {\mathrm{d}}s}{1 - F(x)} \end{aligned}$$

(17)

where f(x) is the probability density function (Weibull in this case) and F(x) is the cumulative distribution.

Multinomial model for assessing nodes in the event trees

We perform Bayesian inference of the $\phi _i$ parameters of the Multinomial distribution. The conditional probability for a multivariate random variable $\phi _i = \{ \phi _1, \phi _2, \ldots , \phi _i, \}$ reads (e.g. Gelman et al. 1995):

$$\begin{aligned} p(y | \phi _i) = { {\sum _{j=1}^i y_j} \atopwithdelims (){y_1 \ldots y_i} } (\phi _1)^{y_1} \ldots (\phi _i)^{y_i} \end{aligned}$$

(18)

where $y = (y_1, \ldots , y_i)$ is the data vector, and the elements $y_i$ are the number of successes (occurrence) relative to the event i with probability $\phi _i$. The sum $\sum _{j=1}^i y_j$ represents the total number of data. i is therefore the number of possible mutually exclusive and exhaustive events in a given node. $L(y | \phi _i)$ is the marginal distribution of $\phi _i$. Note that the case $i=2$ is equivalent to the binomial distribution.

The conjugate Prior for the Multinomial distribution is the Dirichlet distribution (e.g. Gelman et al. 1995), which for a generic multivariate random variable $\phi _i$ reads:

$$\begin{aligned} \pi _0(\phi _i) = \frac{\varGamma (\alpha _1 + \cdots + \alpha _i)}{\varGamma (\alpha _1)\ldots \varGamma (\alpha _i)} [\phi _1]^{\alpha _1 - 1} \ldots [\phi _i]^{\alpha _i - 1} \end{aligned}$$

(19)

where $\varGamma ()$ is the Gamma function, $\alpha _i>0$, $\phi _i>0$, and $\sum _{j=1}^i \phi _j = 1$, with i the number of possible mutually exclusive and exhaustive events. Since the random variable is a probability, the Dirichlet distribution is particularly suitable, being unimodal and with domain [0, 1] in each variate.

To set the model parameters of the prior distribution we follow a similar approach as the one used for the binomial model. To set the parameters of the Dirichlet prior distribution we adopt the same approach presented for the beta distribution (Marzocchi et al. 2008) in which the analyst set the prior state of knowledge by defining (1) a mean value, $\theta _i$, as the best estimate of the $\theta$ parameters, and (2) an uncertainty order of magnitude, using the so-called equivalent sample size, $\varLambda , \varLambda >0$. As stated before, $\varLambda$ is a number representing the quantity of data that the analyst expects to have in order to modify the prior beliefs regarding the parameter. Once $\theta$ and $\varLambda$ have been set, the parameters of the Dirichlet distribution can be set solving the following set of equations (Marzocchi et al. 2008):

$$\begin{aligned} \left\{ \begin{array}{ll} &{}\theta _i = \frac{\alpha _i}{\sum _{j=1}^i \alpha _j} \\ &{}\varLambda = \left[ \sum \nolimits _{j=1}^i \alpha _j \right] -i + 1 \\ \end{array} \right. \end{aligned}$$

(20)

The posterior distribution, $\pi _1(\theta |E)$, for the Multinomial-Dirichlet conjugate pair is the Dirichlet distribution:

$$\begin{aligned} \pi _i(\phi _i|E) = \frac{\varGamma (\alpha '_1 + \cdots + \alpha '_i)}{\varGamma (\alpha '_1)\ldots \varGamma (\alpha '_i)} [\phi _1]^{\alpha '_1 - 1} \ldots [\phi _i]^{\alpha '_i - 1} \end{aligned}$$

(21)

where:

$$\begin{aligned} \alpha '_i = \alpha _i + y_i. \end{aligned}$$

(22)

Appendix 2: Considering external perturbations through physical reliability models (PRM)

Static PRM

We use Static PRM as a basic template for assessing the failure probabilities of elements exposed to (mainly) external hazards. To provide a generic description we take as reference the Random Shock-Loading model (e.g. Ebeling 1997; Hall and Strutt 2003). It is assumed that a variable stress load L is applied, at random times, to an element (e.g. a mechanical component or infrastructural element) of given strength. Stresses are often considered as physical or chemical parameters affecting the component’s operation. Strength is defined as the highest amount of stress that the component can bear. According to the definition of stress and strength, a failure occurs when the stress on the component exceeds its strength (Ebeling 1997; Hall and Strutt 2003). Both stress and strength can be constant or considered as random variables having probability distribution functions. For example, the failure probability of component Q having a constant strength k, and being under random load, L, can be defined as the probability of Y being greater than k (see, e.g. Ebeling 1997; Hall and Strutt 2003; Khakzad et al. 2012):

$$\begin{aligned} {\mathrm{Pr}}(L>k) = \int _k^\infty f_{\mathrm{L}}(l) {\mathrm{d}}l \end{aligned}$$

(23)

where $f_{\mathrm{L}}(l)$ is the probability density function of the stress L (see, e.g. Khakzad et al. 2012). It is also possible to assume an uncertainty in the strength limit k; in such a case, the limit strength is therefore characterised by a probability density function $f_{\mathrm{S}}(k|l)$. Such a function can be understood in similar way as the fragility functions developed for seismic risk analyses. On the other hand, stress variables in this case are equivalent to the intensity measure (IM) usually used for hazard assessment in probabilistic frameworks [see, for example, hazard assessments associated with seismic occurrences (e.g. Cornell 1968), tsunami waves (Davies et al. 2018), extreme meteorological events (e.g. Garcia-Aristizabal et al. 2015), etc.]. Therefore, the stress function can be basically defined using the output of probabilistic hazard assessments.

Dynamic PRM

Dynamic PRMs aim to explain the event occurrence (e.g. the failure of a component) as a multivariate function of operational physical parameters (e.g. Ebeling 1997; Khakzad et al. 2012). The dynamic PRMs in the MHR approach are implemented considering two special cases assuming that it is possible to identify a relationship between (1) operational parameters of interest and the rate of occurrence of events stressing the system (i.e. hazard); (2) operational parameters of interest and the strength of components of interest.

Covariates linked to the stress component:

In this case, the covariate model for assessing the probability of having a determined damage state ($D_{\mathrm{n}}$, as, e.g. a failure) can be written as:

$$\begin{aligned} {\mathrm{Pr}}(D_{\mathrm{n}}) = \int g(D_{\mathrm{n}} | l) f_{\mathrm{L}}(l | \mu _i(\theta )) {\mathrm{d}}l \end{aligned}$$

(24)

where $f_{\mathrm{L}}(l | \mu_i (\theta ))$ is the probability distribution of the loads stressing the system, whose parameters are a function of the covariates; $\theta$ is the vector of covariates, $\mu _i$ is the ith parameter of the probabilistic model $f_{\mathrm{L}}()$ that depends on the defined covariates $\theta$; $g(D_{\mathrm{n}} | l)$ is the probability distribution associated with the occurrence of the damage state $D_{\mathrm{n}}$ given the stress l (intensity measure). In this case, therefore, we assume that the rate of occurrence of the loading process (hazard) is changing as a function of a covariate of interest. An example of the implementation of such a covariate model can be consulted in Garcia-Aristizabal (2018).

Covariates linked to the strength component

In this case the covariates are associated with the distribution that characterises the probability of having a given damage state (e.g. failure) of a given element of interest. It is defined as (e.g. Khakzad et al. 2012; Hall and Strutt 2003):

$$\begin{aligned} {\mathrm{Pr}}(D_{\mathrm{n}}) = \int g(D_{\mathrm{n}} | l, \theta ) f_{\mathrm{L}}(l) {\mathrm{d}}l \end{aligned}$$

(25)

where $g(D_{\mathrm{n}} | l, \theta )$ is the probability distribution associated with having the damage state $D_{\mathrm{n}}$ given the stress l (intensity measure) and the covariates $\theta$.

Appendix 3: Algorithms implemented for solving FTs and ETs

FT analysis

Analytic methods for evaluating a FT usually express the whole tree in terms of a set of minimal cut sets (a cut set is a set of components that can together cause the system to fail; see, e.g. Lee et al. 1985; Carrasco and Sune 1999; Ferdous et al. 2007; Ruijters and Stoelinga 2015). The analysis of complex FTs with large number of minimal cut sets can be performed using a Monte Carlo approach (e.g. Rao et al. 2009; Taheriyoun and Moradinejad 2014; Ruijters and Stoelinga 2015). Monte Carlo methods constitute a class of algorithms based on repeated random sampling of input parameters to compute a required output. The algorithm implemented in MERGER for evaluating FTs is based on a general template often used by Monte Carlo based methods for solving FT structures, as the one presented, e.g. in Han and Lim (2012).

The algorithm for the FT analysis consists of randomly determining the state of each BE and calculating the state of the TE using the FT logic. The state of the TE of a FT can be expressed as a function of BEs as (Han and Lim 2012; Taheriyoun and Moradinejad 2014):

$$\begin{aligned} T = f({\mathrm{BE}}_i) = f({\mathrm{BE}}_1, {\mathrm{BE}}_2, \ldots , {\mathrm{BE}}_n) \end{aligned}$$

(26)

where T is a TE of a FT, f() represents the FT logical equations, and ${\mathrm{BE}}_i$ is the vector of the FT’s BEs. The state of all BEs and their occurrence probabilities are represented as:

$$\begin{aligned} S_{{\mathrm{T}}} = (S_1, S_2, \ldots , S_n) \end{aligned}$$

(27)

where $S_i$ is the state of the ith BE, whose state in a given trial iteration can be false (0) or true (1) (Han and Lim 2012). The probability that $S_i =$true corresponds with the probability of the ith BE, $p_i$.

The probability of T is stochastically determined by sampling the state of the BEs based on their occurrence probabilities and propagating their states to determine the state of the TE. In practice, inserting the state vector $S_{{\mathrm{T}}}$ into Eq. 26 at each trial iteration allows us to find the state of the TE. By repeating this process a sufficient number of times ($n_{\mathrm{t}}$ trials), the probability of the TE can be asymptotically obtained by the fraction $m/n_{\mathrm{t}}$, where m is the number of top event’s true states found out of $n_{\mathrm{t}}$ trials (Han and Lim 2012).

In our approach, the $p_i$ of the BEs are not simple probability values; rather, we define probability distributions defined over each BE’s probability value. In this way, the modelling uncertainties associated with the BE’s definition are taken into account in the analysis. Therefore, in our approach the Monte Carlo algorithm previously described is iterated $N_{{\rm s}}$ times; in each iteration the $p_i$ is sampled from the distributions defined for each ${\mathrm{BE}}_i$, obtaining in this way $N_{{\rm s}}$ realisations of the TE probability, $P_{{\mathrm{T}}}$.

The following algorithm, based on the one presented in Han and Lim (2012), summarises the two key functions implemented in the MERGER system for analysing the FTs.

(i) Function to evaluate Top Event Probability, $[P_{{\mathrm{T}}}]$:

• Set $N_\mathrm{s}$: number of iterations;

• Set $n_\mathrm{t}$: number of trials (within each iteration);

• for the number of iterations $N_\mathrm{s}$ do (j):

  • set $m=0$ (number of TE true states);

  • Sample $p_i$ from the ${\mathrm{BE}}_i$ distribution (for all the BE defined);

  • for the number of trials $n_{\mathrm{t}}$ do (k):

    • Randomly determine the state of each BE:

         $*$ sample a random number $r_{i,k}$: $0\le r_{i,k} \le 1$

         $*$ if $r_{i,k}\le p_i$: then $S_{i,k}=$ true

         $*$ else: then $S_{i,k}=$ false

    • Calculate the jth state of the top event ($S_{{\mathrm{T}}_j}$):

         $*$$S_{{\mathrm{T}}_k}$ = GetTopEvState$[f(S_{:,k})]$

         $*$ if $S_{{{\mathrm{T}}}_k} =$ true, then: $m=m+1$

  • Evaluate the jth TE probability:

    • $P_{{{\mathrm{T}}}_j} = \frac{m}{n_{\mathrm{t}}}$ (see also Eq. 29 for optimisation)

• Return $[P_{{\mathrm{T}}}]$ samples ($N_{\mathrm{s}}$ realisations of $P_{{{\mathrm{T}}}}$)

(ii) Function to get the state of top event

This function, GetTopEvState[f(S)], uses the state $S_i$ of each BE and the logic (gates) defined in the fault tree to determine the jth state of the TE. A FT may contain a large number of intermediate gates to handle the relationships among BEs. To determine the state of the TE, the state of the intermediate gates should be determined. For example, the state of the kth gate, $G_k$, can be calculated based on the states of its inputs:

• if the states of all inputs for an OR gate are False, $G_k$ becomes False; otherwise it becomes True.

• If the states of all inputs for an AND gate are True, $G_k$ becomes True; otherwise it becomes False.

• In MERGER, the fault tree equations are evaluated from bottom to top according to these rules, Assessing:

  • first, the state of intermediate gates whose inputs are all BEs;

  • the state of intermediate gates in which at least one input is an intermediate event (i.e. from the output of another gate);

  • the higher level whose output is the state of the TE.

At each iteration, an approximated value of the TE failure probability $(P_{{{\mathrm{T}}}_j})$ is calculated as the ratio of the number of failures obtained for the TE to the total number of trials: $P_{{{\mathrm{T}}}_j} \approx m/n_{\mathrm{t}}$. The accuracy of this calculation can be assessed by considering the standard error $\epsilon _j$ of this proportion, which for a large number of trials can be defined as $\epsilon _j = \sqrt{P_{{\mathrm{T}}} (1 - P_{{{\mathrm{T}}}_j})/n_{\mathrm{t}}}$. Solving this equation for the number of trials $n_{\mathrm{t}}$, and assuming that the TE probability is small $(P_{{\mathrm{T}}} \ll 1)$, it is possible to determine the expected number of trials for a defined standard error (e.g. Yevkin 2010):

$$\begin{aligned} n_{\mathrm{t}} = \frac{P_{{\mathrm{T}}}}{\epsilon ^2} \end{aligned}$$

(28)

The required number of trials in a given iteration considerably increases as the (desired) standard error decreases. As a reference, Table 9 summarises the required number of trials for different values of $P_{{{\mathrm{T}}}}$ and different reference values for the standard error $\epsilon$ as a percentage of $P_{{{\mathrm{T}}}}$. For example, for a $P_{{{\mathrm{T}}}}$ of the order of $1\times 10^{-2}$, the number of trials required for having a standard error of $\sim 1\%$ of that $P_{{{\mathrm{T}}}}$ is $\sim n_{\mathrm{t}}=1\times 10^{6}$, while for a standard error of $\sim 10\%$ of $P_{{{\mathrm{T}}}}$, $n_{\mathrm{t}}$ must be in the order of $1\times 10^{4}$. In the MERGER system, the $n_{\mathrm{t}}$ is dynamically set in order to ensure a predetermined accuracy level.

Table 9 Estimated number of trials for different values of $P_{{\mathrm{T}}}$ and different reference values for the standard error of $P_{{\mathrm{T}}}$

It is worth noting that this algorithm performs an estimate of $P_{{\mathrm{T}}_j}$ using all the sampled BE states; however, when the BE probabilities are low, a high number of trials results in all the BE set to false; consequently, in such cases the FT will be uselessly evaluated with no TE failures as the outcome. To avoid unnecessary FT evaluations (and therefore to save computational time), an optimisation is implemented so that the FT is evaluated only for trials in which at least one occurring primary event is simulated (see, e.g. Kumamoto et al. 1980; Han and Lim 2012; Taheriyoun and Moradinejad 2014). It means that we can exactly calculate the probability $\gamma$ of having at least one BE defined as true in a set of trials, so that $P_{{{\mathrm{T}}}_j}$ can be calculated as:

$$\begin{aligned} P_{{{\mathrm{T}}}_j} = \gamma \frac{m}{n_{\mathrm{t}}}. \end{aligned}$$

(29)

The Monte Carlo simulation approach for analysing FTs has advantages and disadvantages respect to analytic methods. Among the main advantages we consider that (1) the Monte Carlo method can be easily applied to relatively large FTs, and (2) it allows us to easily set different models for defining BE probabilities, providing adequate flexibility for better describing the different processes involved in the applications of interest. Conversely, among the main disadvantages we can consider that (1) the numerical values obtained by Monte Carlo simulations are approximated solutions whose accuracy strongly depends on the number of trials ($n_{\mathrm{t}}$) performed; when very low probabilities are involved, the number of trials may enormously increase, making the assessments very expensive from a computational perspective; (2) the failure modes generated by Monte Carlo simulations might not be complete, and therefore it is not guaranteed that the cut sets that can be identified are minimal.

ET consequence analysis

The Monte Carlo procedure for the analysis of the ET is based on sampling the distributions used to set each node of the ET, as follows:

• 1. The initiating event (first node), which coincides with the TE of the FT, is sampled by constructing the empirical distribution function using the $N_{\mathrm{s}}$ values of $P_{{\mathrm{T}}}$ generated by the algorithm used for evaluating the FT.

• 2. Nodes with two exhaustive and mutually exclusive branches are defined using the binomial model. Given the Bayesian implementation using conjugate pairs (beta prior/binomial likelihood), the events are randomly sampled form the beta posterior distribution.

• 3. Nodes characterised by more than two exhaustive and mutually exclusive branches are defined using the multinomial model. Given the Bayesian implementation using conjugate pairs (Dirichlet prior/multinomial likelihood), the events in this case are randomly sampled form a Dirichlet posterior distribution.

To calculate the probability of each path of the ET, $N_{\mathrm{et}}$ samples (usually about 1000 samples) are drawn from each distribution (i.e. the ones defined at each node), and the empirical distribution characterising the probability of each path is calculated by using each set of node samples at a time. In this way we obtain $N_{et}$ samples of the probability of each ET’s path, obtaining a numerical approximation of its distribution. Therefore, we propagate both the aleatory and the epistemic uncertainties defined at all nodes. Finally, summary statistics are also provided as output (the median as best estimate of the path probability and two percentiles representing uncertainty ranges).

Appendix 4: Overview of the MERGER system in EPOS

In this section, we briefly describe how to use the application according to its current state of development; nevertheless, the reader is invited to read the user manual available in the platform for more detailed and up-to-date instructions.

Fig. 9

View of the Applications list within the IS-EPOS Platform

In the IS-EPOS Platform, MERGER is available to be used from the Applications menu (Fig. 9). To use any application from the platform it has to be first added to the user’s workspace (using the Add to workspace button; see the quick start guide IS-EPOS 2018).

Once the MERGER application is available in the Workspace, the user can open the application, which at this point is ready to be used. The first step of an assessment is to provide the input data required for quantitative analyses, which in the most general definition can be structured as: (a) the definition of the TE of interest; (b) input/analysis of the Fault Tree, and (c) input/analysis of the Event Tree. At the moment of preparation of this paper, only the FT component of the BT structure of MERGER has been integrated in the IS-EPOS platform. For this reason here we focus on the description of the interface for the construction and analysis of the FT component. It is worth noting that a more detailed description regarding the construction and analyses of the full BT structure will be available in the user manual to be released with the application in the platform.

Fig. 10

View of the Fault tree input/analysis of MERGER (MERGER-FT) within IS-EPOS Platform workspace

Figure 10 shows the interface for inputting data for the FT analysis. In this case, three main inputs are required, namely:

• 1. general information, as the following:

  • Run ID: identification of the application run (used for naming output files);

  • Time-dependent calculations: option to control if it is required to perform the time-dependent calculations;

  • Number of iterations: number of samples to be drawn from the distributions defined for the BEs. This will also be the number of times that the full FT evaluation will be iterated, so it strongly influences the computer time.

  • Mission time: it is the mission time for time-dependent calculations (that is, the time window for the time-dependent probability calculations);

  • Time slices: time points where to write results in time-dependent analysis. To speed up calculations, a low number of time slices should be used

• 2. Definition of basic event’s models, where the user may create all the BEs, by typology, that will be required for constructing the FT. In practice, the user can create any number of BEs for each available class (namely homogeneous Poisson process, on-demand failure, Weibull, static and dynamic physical reliability models). To define a BE of a determined class it is required to provide all the input data (see, e.g. Tables 1, 2, 3 and 4 in the methodology section). Figure 11 shows an example of the interface for adding a BE of class homogeneous Poisson process.

• 3. Definition of fault tree equations; the FT is constructed from BEs (of all the types listed above) or intermediate events ($i_\mathrm{n}$ in Fig. 10, where n is a subsequent number automatically created each time that an intermediate event is defined), joined by logical operators. Intermediate events are created either from BEs or from other in intermediate events. The end point of the tree is the critical TE (te in Fig. 10), which is constructed in the same way as intermediate events, but marked with a property of being the top-most event (which indicates that the higher level of the tree has been reached).

Fig. 11

Detailed view of MERGER-FT application: homogeneous Poisson process basic events input within IS-EPOS Platform workspace

Fig. 12

View of one of the FT-MERGER outputs within IS-EPOS Platform workspace. One of the outputs is displayed directly in the workspace, others are visible as files in the workspace tree on the left

After specifying the FT inputs and running the application (the button Run), the MERGER software is executed on distributed computing resources. The computation itself may take some time, depending on the complexity of the fault tree and on the number of iterations supplied as one of the input parameters. After the computation is finished, the results of the application are saved to the user’s Workspace and is available to be displayed (see, e.g. Fig. 12) or downloaded. The application run is asynchronous; therefore, the results will be saved even if the user is not logged-in to the IS-EPOS Platform. This is a very important feature, especially when analysing large, complex problems, because in the case of computationally expensive analyses, the user can launch calculations, log-off of the system, and retrieve the results after some time by logging-in again into the platform.